Frešeova razdaljina
U matematici, Frešeova razdaljina je mera sličnosti između krivih koja uzima u obzir lokacije i redosled tačaka na krivama. Dobila je ime po Morisu Frešeu.
Intuitivna definicija[uredi | uredi izvor]
Frešeova razdaljina između 2 krive je minimalna dužina povoca potrebna da se povežu pas i njegov vlasnik, smeštenih na 2 odvojene staze, dok se kreću isključivo napred duž svojih pojedinačnih putanja od jednog kraja do drugog. Definicija je simetrična u odnosu na dve krive. Zamislite psa kako ide jednom putanjom i njegovog vlasnika kako ide drugom putanjom, a povezani su povocem. Oboje se kreću neprekidno duž svojih pojedinačnih krivih od predviđene početne tačke do predviđene krajnje tačke putanje. Brzina obojice varira, mogu i da stanu, na proizvoljnoj poziciji i na proizvoljno dugo vreme. Međutim, moraju se isključivo kretati napred. Frešeova razdaljina između 2 krive je dužina najkraćeg povoca (ne najkraćeg povoca koji je dovoljan za bilo kakvo kretanje, već najkraćeg od svih povodaca) koji je dovoljan da se povežu obe krive na ovaj način.
Formalna definicija[uredi | uredi izvor]
Neka je metrički prostor. Kriva u je neprekidna funkcija iz jediničnog intervala u , npr., . A, reparametrizacija iz je neprekidna, monotona funkcija, surjekcija .
Neka su i dve date krive . Onda, Frešeova razdaljina između i se definiše kao infimum svih reparametrizacija i iz maksimuma od svih razdaljina u između i . U matematičkom zapisu, Frešeova razdaljina je
gde je funkcija razdaljine u .
Neformalno, možemo da posmatramo parametar kao "vreme". Onda, je pozicija psa, a pozicija njegovog vlasnika u trenutku (ili obrnuto). Dužina povoca između njih u trenutku je rastojanje između i . Infimum svih mogućih reparametrizacija odgovara odabiru kretanja duž datih staza gde je maksimalna dužina povoca najmanja moguća. Ograničenje da su i neopadajuće znači da se i pas i njegov vlasnik mogu kretati isključivo napred.
Frešeova metrika uzima u obzir putanje 2 krive zato što parovi tačaka čija razdaljina doprinosi Frešeovoj razdaljini neprekidno klize duž pojedinačnih krivih. To čini Frešeovu razdaljinu boljom merom sličnosti za krive nego alternative, kao što je Hausdorfova razdaljina, za proizvoljne nizove tačaka. Moguće je da 2 krive imaju malu Hausdorfovu, a veliku Frešeovu razdaljinu.
Frešeova razdaljina i njene varijante imaju primenu u nekoliko problema, od specijalnih efekata za filmove i animacije[1] i prepoznavanja rukopisa[2] do usklađivanja strukture proteina.[3] Alt i Godo[4] su prvi opisali algoritam u polinomskom vremenu da bi izračunali Frešeovu razdaljinu između 2 poligonske krive i Euklidovom prostoru. Vreme izvršavanja njihovog algoritma je za 2 poligonske krive sa m i n segmentima.
Dijagram u slobodnom prostoru[uredi | uredi izvor]
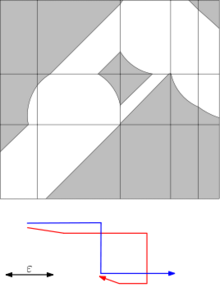
Važan način računanja Frešeove razdaljine 2 krive je dijagram u slobodnom prostoru koji su prvi uveli Alt i Godo.[4] Dijagram u slobodnom prostoru između 2 krive za dati prag razdaljine ε je dvodimenzionalna oblast u parametarskom prostoru koji se sastoji od svih parova tačaka na 2 krive najvećeg rastojanja ε:
Frešeova razdaljina je najviše ε ako i samo ako dijagram u slobodnom prostoru sadrži putanju od donjeg levog do gornjeg desnog ugla, koji je monoton i u horizontalnom i u vertikalnom pravcu.
Varijante[uredi | uredi izvor]
Slaba Frešeova razdaljina je varijanta klasične frešeove razdaljine bez uslova da se krajnje tačke kreću monotono duž svojih krivih — pcu i njegovom vlasniku je dozvoljeno da se vraćaju nazad da bi održali povodac kratkim. Alt i Godo[4] su opisali jednostavniji algoritam za izračunavanje slabe Frešeove razdaljine između poligonalnih krivih.
Diskretna Frešeova razdaljina, takozvana pazdaljina spojnice, je aproksimacija Frešeove metrike za poligonske krive, koje su definisanali Ajter i Manila.[5] Diskretna Frešeova razdaljina razmatra samo pozicije užeta gde su njegove krajnje tačke locirane na temenima 2 poligonske krive i nikada u unutrašnjosti ivice. Ova specijalna struktura dozvoljava da se diskretna Frešeova razdaljina izračuna u polinomnom vremenu lakim algoritmom dinamičkog programiranja.
Kada su dve krive ugrađene u metrički prostor izuzev Euklidovog prostora, kao što je poliedarskih teren ili neki Euklidov prostor sa preprekama, rastojanje između dve tačke na krivama najprirodnije se definiše kao dužina najkraćeg puta između njih. Povodac mora da bude geodetski spoj njegovih krajnjih tačaka. Dobijena metrika između krivih se zove geodetsko Frešeovo rastojanje.[1][6][7] Kuk i Venk[6] su opisali algoritam za računanje Frešeove razdaljine između 2 poligonske krive u mnogouglu sa nepresecajućim stranicama u poligonalnom vremenu.
Ako povodac mora neprekidno da se kreće u ambijentalnom metričkom prostoru, onda dobijamo homotopijsku Frešeovu razdaljinu[8] između 2 krive. Povodac se može prebaciti sa jedne pozicije jedino neprekidno u drugi, ali povodac ne može preskočiti prepreke, a može preći preko planine na terenu samo ako je dovoljno dug. Kretanje povoca opisuje homotopiju između dve krive. Čambers i ostali opisujualgoritam u polinomnom vremenu za izračunavanje homotopijske Frešeove razdaljine između poligonalnih krivih u Euklidovoj ravni sa preprekama.
Primeri[uredi | uredi izvor]
Frešeovo rastojanje između 2 koncentrična kruga poluprečnika i je Najduži povodac je potreban kada vlasnik stoji a pas ode na suprotnu stranu kruga (), a najkraći povodac je kada se obojica kreću konstantnom brzinom oko kruga ().
Reference[uredi | uredi izvor]
- ^ a b Efrat, Alon; Guibas, Leonidas J.; Har-Peled, Sariel; Mitchell, Joseph S. B.; Murali, T. M. (2002), „New similarity measures between polylines with applications to morphing and polygon sweeping” (PDF), Discrete and Computational Geometry, 28 (4): 535—569, doi:10.1007/s00454-002-2886-1, Arhivirano iz originala (PDF) 19. 06. 2010. g., Pristupljeno 08. 06. 2014
- ^ Sriraghavendra, R.; Karthik, K.; Bhattacharyya, Chiranjib (2007), „Fréchet distance based approach for searching online handwritten documents”, Proc. 9th International Conference on Document Analysis and Recognition (ICDAR '07), str. 461—465, doi:10.1109/ICDAR.2007.121, Arhivirano iz originala 03. 03. 2016. g., Pristupljeno 08. 06. 2014
- ^ Minghui, Jiang; Ying, Xu; Binhai, Zhu (2008), „Protein structure-structure alignment with discrete Fréchet distance”, Journal of Bioinformatics and Computational Biology, 6 (1): 51—64, PMID 18324745, doi:10.1142/S0219720008003278
- ^ a b v Alt, Helmut; Godau, Michael (1995), „Computing the Fréchet distance between two polygonal curves” (PDF), International Journal of Computational Geometry and Applications, 5 (1–2): 75—91, doi:10.1142/S0218195995000064, Arhivirano iz originala (PDF) 15. 05. 2004. g., Pristupljeno 08. 06. 2014
- ^ Eiter, Thomas; Mannila, Heikki (1994), Computing discrete Fréchet distance (PDF), Tech. Report CD-TR 94/64, Christian Doppler Laboratory for Expert Systems, TU Vienna, Austria
- ^ a b Cook, Atlas F., IV; Wenk, Carola (2008), Geodesic Fréchet distance with polygonal obstacles (PDF), Tech. Report CS-TR-2008-0010, University of Texas at San Antonio[mrtva veza]
- ^ Maheshwari, Anil; Yi, Jiehua (2005), „On computing Fréchet distance of two paths on a convex polyhedron”, Proc. 21st European Workshop on Computational Geometry (PDF), str. 41—44, Arhivirano iz originala (PDF) 03. 03. 2016. g., Pristupljeno 08. 06. 2014
- ^ Chambers, Erin Wolf; Colin de Verdière, Éric; Erickson, Jeff; Lazard, Sylvain; Lazarus, Francis; Thite, Shripad (2009), „Homotopic Fréchet distance between curves, or Walking your dog in the woods in polynomial time” (PDF), Computational Geometry: Theory and Applications, 43 (3): 295—311, doi:10.1016/j.comgeo.2009.02.008[mrtva veza]



![{\displaystyle A:[0,1]\rightarrow S}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6edd4c77af36de6c609ab6800cce5f57c21742e)

![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
![{\displaystyle \alpha :[0,1]\rightarrow [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3670292977d70d09aa06595f56abffe9173dfa8f)


![{\displaystyle t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a5c18739ff04858eecc8fec2f53912c348e0e5)



![{\displaystyle F(A,B)=\inf _{\alpha ,\beta }\,\,\max _{t\in [0,1]}\,\,{\Bigg \{}d{\Big (}A(\alpha (t)),\,B(\beta (t)){\Big )}{\Bigg \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3395e48df64fa6870dcdc64f6992558789a2a1f7)



![{\displaystyle D_{\varepsilon }(A,B):=\{\,(\alpha ,\beta )\in [0,1]^{2}\mid d(A(\alpha ),B(\beta ))\leq \varepsilon \,\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5528eadf0a7d67fe052cdcf26a27b5a350b19b5)





