Нортонова теорема
У Европи позната као Мајер-Нортонова теорема, Нортонова теорема служи да за описивање следећих својства електричних кола (погледати слику):
- Било која линеарно електрично коло са напонским и струјним изворима и само отпорницима може да се замени на својим прикључцима A-B са еквивалентним струјним извором INO у паралелној вези са еквивалентном отпорношћу RNO.
- Ова еквивалентна струја INO је струја која се добија са прикључака A-B електричног кола које је кратко спојено (отпор 0) на својим прикључцима A-B.
- Добијени еквивалентни отпор RNO је отпор који се добија на прикључцима A-B електричног кола када су сви његови напонски извори кратко спојени, а сви струјни извори неповезани.
За кола са наизменичном струјом, теорема је употребљива за реактивну снагу, импедансе и резистансе.
Еквивалентно Нортоново електрично коло се користи да представи било које електрично коло које се садржи од линеарних извора на датој фреквенцији.

Нортонова теорема, и њој слична Тевененова теорема, се често користе у поједностављењу анализе електричних кола као и за проучавање почетних стања кола и одзива на промене.
До Нортонове теореме су независно надошли 1926, године Сименсов истраживач Ханс Фердинад Мејер и инжењер из Бел лабораторија Едвард Лаври Нортон.[1][2][3][4][5]
Да би се израчунало Нортоново еквивалентно електрично коло,
- Наћи Нортонову струју INo. Израчунати излазну струју IAB, са кратким спојем као спољним оптерећењем електричног кола (отпором 0 између прикључака A и B). Ово даје струју INo.
- Израчунати Нортонов отпор RNo. Када не постоје зависни извори унутар кола (сви струјни и напонски извори су независни), постоје две методе за утврђивање Нортонове импедансе RNo.
- Израчунати излазни напон, VAB, када се коло налази у отвореном стању (отпор је бесконачно велики).RNo је једнак VAB подељеном струјом INo.
- или
- Заменити независне напонске изворе кратким спојем, а независне струјне изворе отвореним колом. Укупан отпор на прикључцима A-B биће једнак Нортоновој импеданси RNo.
Ово је еквивалентно израчунавању еквивалентног Тевененовог отпора.
- Али уколико постоје зависни извори, треба користити општију методу. Ова метода није приказана на сликама испод.
- Повезати константан извор струје на излазне прикључке електричног кола који има вредност струје од 1 Ампера и израчунати напон на прикључцима. Овај напон подељен струјом од 1 А је Нортонова импеданса RNo. Ова метода се мора користити уколико коло садржи зависне изворе, али може да се користи у свим случајевима чак и када нема зависних извора.
Пример еквивалентног Нортоновог електричног кола[уреди | уреди извор]
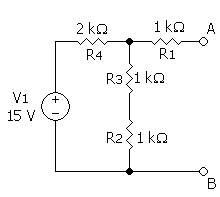 |
 |
 |

У примеру, укупна струја Itotal је дата са:
Струја кроз оптерећење је онда једнака (коришћењем струјног разделника):
Еквивалентна отпорност једнака је:
Добија се да се еквивалентно електрично коло састоји из извора струје који даје 3,75мА у паралели са отпорником од 2 kΩ.
Конверзија у еквивалентно Тевененово електрично коло[уреди | уреди извор]
Еквивалентно Нортоново електрично коло је у односу са еквивалентним Тевененовим електричним колом на следећи начин:
Види још[уреди | уреди извор]
Референце[уреди | уреди извор]
Литература[уреди | уреди извор]
- Brittain, J.E. (1990). „Thevenin's theorem”. IEEE Spectrum. 27 (3): 42. doi:10.1109/6.48845. Приступљено 1. 2. 2013.
- Chandy, K. M.; Herzog, U.; Woo, L. (1975). „Parametric Analysis of Queuing Networks”. IBM Journal of Research and Development. 19 (1): 36—42. doi:10.1147/rd.191.0036. Архивирано из оригинала 25. 12. 2021. г. Приступљено 07. 01. 2022.
- Dorf, Richard C.; Svoboda, James A. (2010). „Chapter 5 – Circuit Theorems”. Introduction to Electric Circuits (8th изд.). Hoboken, NJ: John Wiley & Sons. стр. 162—207. ISBN 978-0-470-52157-1. Архивирано из оригинала 30. 04. 2012. г. Приступљено 10. 11. 2013.
- Gunther, N.J. (2004). Analyzing computer systems performance : with PERL::PDQ (Online-Ausg. изд.). Berlin: Springer. стр. 281—. ISBN 978-3-540-20865-5.
- Johnson, D.H. (2003). „Origins of the equivalent circuit concept: the voltage-source equivalent” (PDF). Proceedings of the IEEE. 91 (4): 636—640. doi:10.1109/JPROC.2003.811716.
- Johnson, D.H. (2003). „Origins of the equivalent circuit concept: the current-source equivalent” (PDF). Proceedings of the IEEE. 91 (5): 817—821. doi:10.1109/JPROC.2003.811795.
- Mayer, H. F. (1926). „Ueber das Ersatzschema der Verstärkerröhre (On equivalent circuits for electronic amplifiers]”. Telegraphen- und Fernsprech-Technik. 15: 335—337.
- Norton, E. L. (1926). „Technical Report TM26–0–1860 – Design of finite networks for uniform frequency characteristic”. Bell Laboratories.







