Хомоморфизам
Хомоморфизам (од грч. homós - исти, грч. morphe - облик, форма) у математици представља пресликавање између две алгебарске структуре истог типа, које чува њихову форму.
Особине[уреди | уреди извор]
Нека су и две алгебарске структуре истог типа (група, поље, моноид итд.). Ако је пресликавање хомоморфизам а важиће:
Врсте хомоморфизама[уреди | уреди извор]
- Изоморфизам је бијективни хомоморфизам. Два објекта су изоморфна ако постоји изоморфизам између њих. Изоморфни објекти су потпуно неразазнатљиви што се тиче структуре која је у питању.
- Епиморфизам је сурјективни хомоморфизам.
- Мономорфизам је инјективни хомоморфизам.
- Хомоморфизам са неког објекта на самог себе се зове ендоморфизам.
- Ендоморфизам који је и изоморфизам се зове аутоморфизам.
У ширем контексту пресликавања која чувају структуру, начелно није довољно дефинисати изоморфизам као бијективни морфизам. Потребан услов је и да је инверзни морфизам истог типа. У алгебарским условима, овај додатни услов је аутоматски задовољен.
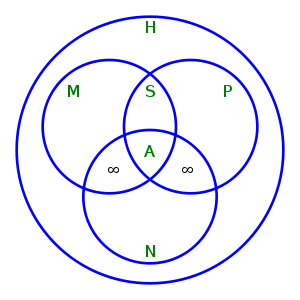
- Односи између различитих врста хомоморфизама.
H = скуп хомоморфизама, M = скуп мономорфизама,
P = скуп епиморфизама, S = скуп изоморфизама,
N = скуп ендоморфизама, A = скуп аутоморфизама.
Приметити да: M ∩ P = S, S ∩ N = A, док класе
M ∩ N \ A и P ∩ N \ A могу бити непразне једино у случају бесконачних група.
Литература[уреди | уреди извор]
- Ayres, Frank (1965). Schaum's Outline of Modern Abstract Algebra. McGraw-Hill; 1st edition (June 1, ). ISBN 978-0-07-002655-1.






