Алгоритам обрнутог брисања

Алгоритам обрнутог брисања је алгоритам у теорији графова који се користи за добијање минималног разапињућег стабла из датог повезаног тежинскоg графа . Он се први пут појавио kод Kрускалa 1956, али то не треба мешати са алгоритмом Крускала који се помиње у овој области. Уколико граф није повезан, овај алгоритам ће наћи минимално разапињуће стабло, одвојено за сваки део графа. Скуп ових минималних разапињућих стабала се зове минимална разапињућа шума, која садржи сваки чвор графа.^[1]^[2]

Овај алгоритам је похлепни алгоритам, бира најбољи избор у сваком тренутку у задатој ситуацији. То је супротно од Крускаловог алгоритма, што је још један похлепни алгоритам који проналази минимално Разапињуће стабло. Крускалов алгоритам почиње са празним графом и додаје гране, док обрнуто брисање почиње са оригиналном графом и брише из њега гране. Алгоритам ради на следећи начин:

Почиње са графом Г, који садржи листу грана Е.
Иде до Е по опадајућем редоследу тежине грана.
За сваку грану, проверите да ли ће брисање направити неповезан граф.
Извршите брисања која не доводе до додатних искључења.

Псеудокод[уреди | уреди извор]

 1  function ReverseDelete(edges[] E)
 2    sort E in decreasing order
 3    Define an index i ← 0
 4    while i < size(E)
 5       Define edge temp ← E[i]
 6	   delete E[i]
 7	   if temp.v1 is not connected to temp.v2
 8             E[i] ← temp
 9   	   i ← i + 1
 10   return edges[] E

Горњи граф је скуп грана Е где свака грана има тежину и повезује чворове v1 и v2.

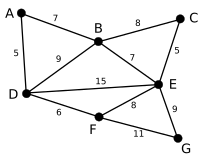
Пример[уреди | уреди извор]

У следећем примеру зелене гране се процењују у алгоритму а црвене гране су избрисане.

	Ово је наш оригинални граф. Бројеви на грани говоре тежину гране.
	Алгоритам ће почети са граном максималне тежине, што је у ово случају DE тежине 15. Пошто брисање грана DE не узрокује распадање графа, грана се брише.
	Следећа највећа грана је FG , алгоритам ће проверити да ли брисањем ове гране долази до распада графа. Пошто брисање гране неће довести дотле, грана је тада обрисана.
	Следећа највећа грана је BD, па ће алгоритам проверити ову грану и избрисати је.
	Следећа грана је да проверите грану EG, која неће бити избрисана јер би искључили чвор G из графа. Дакле, следећа грана за брисање је BC.
	Следећа највећа грама је грана ЕF, тако ће алгоритам проверити ову грану и избрисати је.
	Алгоритам ће онда тражити преостале гране и неће наћи другу грану да обрише, па ово је коначни граф који нам враћа алгоритам.

Време извршавања[уреди | уреди извор]

За алгоритам се може доказати да ради у О (E log V (log log V)³) времену, где јеЕ је број грама и V је број чворова. Ова граница се достиже на следећи начин:^[3]

Сортирање грана по тежини помоћу поређења у О ( Е лог Е) времену
Е итерације петље
Брисање уО (1) времену
Повезивање проверити у O(logV (log log V)³) времену Thorup 2000.

Исто тако, време рада може се сматрати О (E log E (log log E)³) јер највећи Е може се V ². Запамтите да logV ² = 2 * log V, па 2 је мултипликативна константа која ће бити игнорисана у нотацији великог O.

Референце[уреди | уреди извор]

^ Kleinberg, Jon; Tardos, Éva (2006), Algorithm Design, New York: Pearson Education, Inc.
^ Kruskal, Joseph B. (1956), „On the shortest spanning subtree of a graph and the traveling salesman problem”, Proceedings of the American Mathematical Society, 7 (1): 48—50, JSTOR 2033241
^ Thorup, Mikkel (2000), „Near-optimal fully-dynamic graph connectivity”, Proc. 32nd ACM Symposium on Theory of Computing, стр. 343—350, doi:10.1145/335305.335345

[1] Kleinberg, Jon; Tardos, Éva (2006), Algorithm Design, New York: Pearson Education, Inc.

[2] Kruskal, Joseph B. (1956), „On the shortest spanning subtree of a graph and the traveling salesman problem”, Proceedings of the American Mathematical Society, 7 (1): 48—50, JSTOR 2033241

[3] Thorup, Mikkel (2000), „Near-optimal fully-dynamic graph connectivity”, Proc. 32nd ACM Symposium on Theory of Computing, стр. 343—350, doi:10.1145/335305.335345

[1]

[2]

[3]