Dijagram stanja

Dijagram stanja je dijagram koji se koristi na polju kompjuterskih nauka, koji predstavlja ponašanje sistema koji je sastavljen od konačnog broja stanja. Postoje mnogi oblici dijagrama stanja, koji se neznatno razlikuju i imaju različitu semantiku.

Pregled[uredi | uredi izvor]

Dijagrami stanja se koriste za opisivanje ponašanja sistema. Oni mogu da opišu moguća stanja objekta kako se događaji pojavljuju. Svaki dijagram obično predstavlja objekte jedne klase i prati različita stanja tih objekata kroz sistem.

Dijagram stanja se može upotrebiti da grafički predstavi automate konačnih stanja. Ovo je predstavljeno od strane Tejlora Buta(Taylor Booth) u njegovoj knjizi iz 1967. godine “ Sequential Machines and Automata Theory”. Drugi mogući način predstavljanja je preko tabele promene stanja.

Usmereni graf[uredi | uredi izvor]

Klasična forma dijagrama stanja za predstavljanje konačnih automata je usmereni graf sa sledećim elementima:

Stanja Q: konačan skup vertices normalno predstavljenih krugovima i označenih simbolima ili rečima napisanim unutar njih;
Ulazni simboli S: konačna kolekcija ulaznih simbola ili designators;
Izlazni simboli Z: konačna kolekcija izlaznih simbola ili designators;

Izlazna funkcija ω predstavlja mapiranje ulaznih simbola u izlazne, predstavljenu matematički kao ω : Σ × Q → Z.

Ivice δ: predstavlja prelaze između dva stanja nastale unosom (identifikovane preko svojih simbola nacrtanih na ivicama). Ivica se obično crta kao strelica usmerena od sadašnjeg stanja prema narednom stanju. Ovo mapiranje opisuje promene stanja koje bi trebalo da nastanu pri unosu određenog simbola. Ovo se matematički zapisuje kao δ : Σ × Q → Z
Početno stanje q0: (nije prikazano u primerima koji slede). Početno stanje q0 ∈ Q je obično prikazano kao strelica kojoj ne prethodi stanje usmerena na neko stanje. U starijim tekstovima, početno stanje nije prikazano i mora se zaključiti iz teksta.
Završno stanje(stanja) F: ako se koristi npr. za završavanje automata, F ∈ Q je završno stanje. Obično se crta kao dva kruga. Ponekad završno stanje(stanja) funkcionišu kao konačna stanja.

Za determinističke konačne automate (DKA), nedeterminističke automate(NKA), generalizovane nedeterminističke konačne automate (GNKA) ili Murove automate, ulaz je obeležen na svakoj ivici. Za Milijev automat, ulaz i izlaz su označeni na svakoj ivici, razdvojeni kosom crticom “/” : ”1/0”. Za Murov automat izlaz iz stanja je obično napisan unutar kruga kojim je stanje predstavljeno i takođe je odvojeno od designator stanja kosom crtom. Postoje takođe i varijante koje kombinuju ove dve notacije.

Na primer, ako stanje ima određen broj izlaza(e.g. a = motor counter-clockwise = 1, b = caution light inactive = 0) dijagram bi trbao da prikaže sledeće: e.g. „q5 / 1,0“ stanje q5 sa izlazima a=1, b=0. Ovaj designator će biti napisan unutar kruga stanja.

Primer: DKA, NKA, GDKA, ili Murov automat[uredi | uredi izvor]

S1 i S2 su stanja i S1 je završno stanje. Svaka ivica je označena unosom. Ovaj primer pokazuje zatvorenje za string preko {0, 1} koja sadrži čak i određen broj nula.

Primer Milijev automat[uredi | uredi izvor]

S0, S1, S2 su stanja. Svaka ivica je označen sa „j / k“ gde je ј ulaz a к izlaz

Harelov dijagram stanja[uredi | uredi izvor]

Harelovi dijagrami su ušli u široku upotrebu otkad je ova varijanta postala deo Unified modeling Langauge. Ovaj tip dijagrama omogućava modelovanje superstanja, konkurentnih stanja, i aktivnosti kao dela stanja.

Klasični dijagrami stanja su „or“ (disjunkcija) dijagrami, zato što automat može biti samo u jednom od svih mogućih stanja. Sa Harelovim dijagramima je moguće modelovati „and“ automate, gde automat može biti u dva ili više stanja konkurentno. Ovo je moguće zahvaljujući delom modelovanja superstanja i delom modelovanju konkurentnih automata.

UML dijagram stanja[uredi | uredi izvor]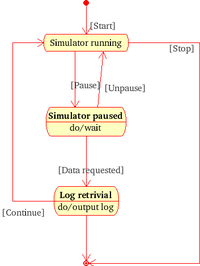

The Unifide Modeling Language(UML) dijagram stanja je u osnovi Harelov dijagram sa standardizovanoim notacijama, koji može opisati mnoge sisteme, od kompjuterskih programa do biznis procesa. Ono što sledi su osnovni notacioni elementi koji se mogu koristiti da se napravi dijagram:

Ispunjen krug koji pokazuje inicijalno stanje
Prazan krug koji sadrži manji ispunjen krug, pokazujući završno stanje(ako ga ima)
Zaobljeni pravougaonik označava stanje. Vrh pravougaonika sadrži ime stanja. Može sadržati horizontalnu liniju u sredini, ispod koje su prikazane aktivnosti koje su urađeni u tom stanju.
Strelica koja označava prelaz. Ime događaja(ako postoji) koji uzrokuje ovu promenu napisan je duž strelice. Gard izrazi mogu da se dodaju ispred “/” (eventName[guardExpression]) označavajući da ova izraz mora biti istinit da bi se prelaz odigrao. Ako se tokom ovog prelaza dešava neka radnja, to se dodaje oznaci iza kose crte (eventName[guardExpression]/action).
Tanka horizontalna linija sa ili x>1 ulaznih linija i 1 izlazna, ili 1 ulazna i više izlaznih linija.

Prema Pilonu (Pilone) jedino predefinisan gard uslov je ELSE. Ni jedan drugi primer nije prikazan u toj publikaciji.

Ostale ekstenzije[uredi | uredi izvor]

Interesantna ekstenzija je dozvoliti lukovima da krenu iz bilo kog broja stanja do bilo kog broja stanja. Ovo ima smisla samo ako je sistemu dozvoljeno da odjednom bude u više stanja što nagoveštava da individualno stanje opisuje uslov ili drugi delimični aspekt celokupnog stanja. Rezultujući formalizam je poznat kao Petrijeva mreža (Petri net).

Druga ekstenzija dozvoljava integraciju dijagrama unutar Harelovog dijagrama stanja.

Vidi još[uredi | uredi izvor]

Literatura[uredi | uredi izvor]

State Diagrams]]., Pristupljeno 11. 8. 2008.
Taylor Booth (1967) Sequential Machines and Automata Theory, John Wiley and Sons, New York.
* Hopcroft, John; Ullman, Jeffrey (1979). Introduction to Automata Theory, Languages, and Computation. Addison-Wesley Publishing Company, Reading Mass. ISBN 978-0-201-02988-8.
Edward J. McClusky, Introduction to the Theory of Switching Circuits, McGraw-Hill, 1965
David Harel, Statecharts: A visual formalism for complex systems. Science of Computer Programming, 8(3):231–274, June 1987.
D. Drusinsky, Modelling and verification using UML statecharts, Elsevier, 2006
Dan Pilone, UML 2.0 Pocket Reference, O'Reilly, 2006

Spoljašnje veze[uredi | uredi izvor]