Žiroskop

Žiroskop (od drev. grčkog γυρο „okret“ i drev. grčkog σκοπεω „posmatrati") je uređaj za merenje promene ugla vezanog za njega tela odnosno inercione sisteme i za održavanje orijentacije. Funkcioniše na osnovu principa ugaonog momenta. Uređaj se sastoji od točka ili diska čija se osovina može slobodno okrenuti u bilo koji položaj prostranstva. Bilo kakva promena položaja ose žiroskopa, usled pridavanja spoljnog momenta, je mnogo manja nego što bi bila bez velikog ugaonog momenta svojstvenog okretljivosti žiroskopa. Zbog minimiziranja spoljašnjeg momenta toniranjem uređaja u kardanski obruč, njegov položaj ostaje gotovo fiksiran, bez obzira na bilo koji pokret platforme na kojoj je montiran.

Dva osnovna tipa žiroskopa:

mehanički
optički (Laserski žiroskop)

Po načinu upotrebe:

merač ugaone brzine
pokazivač pravca

Jedan isti uređaj može da radi u raznim režimima.

Među mehaničkim žiroskopima izdvaja se rotorni žiroskop — brzovrteće tvrdo telo, čija osa okretanja može menjati pravac u prostranstvu. Pritom brzina okretanja žiroskopa mnogokratno premašuje brzinu okretanja njegove ose okretanja. Osnovno svojstvo takvog žiroskopa je sposobnost da u prostranstvu sačuva neizmenjen pravac ose okretanja pri odsustvu dejstva momenata spoljašnjih sila na nju.

Prvi put to svojstvo je iskoristio Žak Bernar Leon 1852. godine, za eksperimentalnu demonstraciju okretanja Zemlje. Baš na toj demonstraciji žiroskop je i dobio svoj naziv, od grčkih reči «okretanje», «posmatranje».

Opis[uredi | uredi izvor]

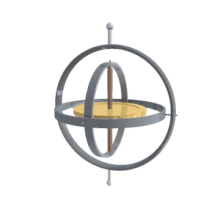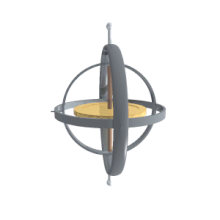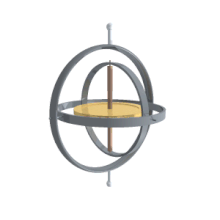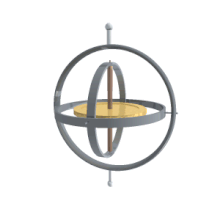
Unutar nekog mehaničkog sistema ili uređaja, konvencionalni žiroskop je mehanizam sastavljen od jednog rotora napravljenog da se vrti oko jedne ose. Nosač rotora se vezuje za unutrašnji kardanski obruč ili prsten, unutrašnji obruč je povezan sa spoljnim obručom koji je privezan za obruč podrške tako da može da se vrti oko svoje ose u ravni određenoj podrškom. Spoljašnji obruč poseduje jedan stepen rotacione slobode. Unutrašnji obruč je montiran na spoljni tako da se okreće oko sopstvene ose u ravni koja je uvek vertikalna osovinskoj osi spoljnjeg obruča.

Osa točka koji rotira opredeljuje osu okretanja. Unutrašnji kardanski obruč poseduje dva stepena slobode, a njegova rotaciona osa poseduje jedan. Rotor je privezan tako da se vrti oko ose koja je uvek vertikalno naspram ose unutrašnjeg obruča. Dakle, rotor poseduje tri stepena rotacione slobode, a njegove ose poseduju dva. Točak odgovara na silu primenjenu oko ulazne ose reakcionom silom oko izlazne ose.

Žiroskopski zamašnjak će se vrteti ili kočiti oko izlazne osovine zavisno od toga da li su izlazni obruči za održavanje instrumenata trenutno slobodni u okretu ili fiksirani.

Gravitacioni centar rotora može biti u fiksiranom položaju. Rotor se vrti istovremeno oko jedne ose i sposoban je oscilovati i oko druge dve ose, te tako, osim zbog naslednog otpora izazvanog okretanjem rotora, može se slobodno okretati u bilo kom smeru oko fiksne tačke. Neki žiroskopi ne koriste mehaničkih princip za jedan ili više elemenata, na primer, rotor može biti potopljen u tečnost, umesto da se montira na kardanski obruč za održavanje instrumenata. Kontroluni momenat žiroskop je primer uređaja fiksiranog izlaznog obruča, koji se koristi na svemirskim brodovima za držanje ili održavanje željenog ugla ili pokazivanje smera pomoću snage otpora žiroskopa.

U posebnim slučajevima, spoljni obruč (ili njegova ekvivalenta) može biti izostavljen tako da rotor ima samo dva stepena slobode. U drugim slučajevima, centar gravitacije rotora može da se poklapa sa osom oscilacije, a samim tim centar gravitacije i centar suspenzije rotora ne moraju se podudarati.

Princip rada[uredi | uredi izvor]

Osnovna, uprošćena, jednačina koja opisuje ponašanje žiroskopa je: ${\boldsymbol {\tau }}={{d\mathbf {L} } \over {dt}}={{d(I{\boldsymbol {\omega }})} \over {dt}}=I{\boldsymbol {\alpha }}$

gde su vektori ${\boldsymbol {\tau }}$ i $\mathbf {L}$ moment žiroskopa i njegov ugaoni momenat, skalar $I\,$ je njegov moment inercije, vektor ${\boldsymbol {\omega }}$ je njegova ugaona brzina, i vektor ${\boldsymbol {\alpha }}$ je njegovo ugaono ubrzanje.

Iz toga sledi da momenat ${\boldsymbol {\tau }}$ primenjen vertikalno na osu rotacije, a time vertikalno i na $\mathbf {L}$ , stvara rotaciju oko ose perpendikularne na oba ${\boldsymbol {\tau }}$ i $\mathbf {L}$ . Ovo kretanje se zove precesija. Ugaona brzina precesije ${\boldsymbol {\Omega }}_{P}$ zavisi od proizvoda vektora: ${\boldsymbol {\tau }}={\boldsymbol {\Omega }}_{P}\times \mathbf {L}$

Precesija se može prodemonstrirati postavljanjem žiroskopa osama horizontalno ka površini i labavo podržanom (nepokretnom odnosno precesije) na jednom kraju. Umesto da pada, kao što se može očekivati, čini se da žiroskop prkosi gravitaciji podržavajući ose horizontalno, dok je druga strana ose ostavljena bez podrške i slobodni kraj ose polako opisuje krug u horizontalnoj ravni, stvarajući okretnu precesiju. Ovaj efekat je objašnjen gorenavedenom jednačinom. Okretni moment na žiroskopu se dobija pomoću dve sile: gravitacije delujući nadole na središte mase uređaja, i jednake sile, delujuće prema gore podržavajući suprotni kraj uređaja. Rotacija koja proizilazi iz ovog momenta nije nadole, kako bi moglo biti intuitivno očekivano, uzrokujući da uređaj padne, a vertikalno na oba gravitacioni moment (horizontalno i vertikalno na osu rotacije) i osu rotacije (horizontalna i dalje od tačke podrške), odnosno oko vertikalne ose, uzrokujući da uređaj polako rotira oko tačke podrške.

Kako druga jednačina prikazuje pod stalnim momentom, brzina precesije žiroskopska je obrnuto proporcionalna svom ugaonom momentu. To znači da, na primer, ako trenje uzrokuje usporavanje okretanja žiroskopa — stopa precesije se povećava. To se nastavlja sve dok uređaj ne može dovoljno brzo da rotira da bi održao sopstvenu težinu. Tada precesija prestaje i uređaj pada sa svoje podrške, uglavnom zbog toga što trenje protiv precesije izaziva drugu precesiju koja nastoji da uzrokuje pad.

Po konvenciji, ova tri vektora, okretni moment, rotacija, i precesija, svi su orijentisani u odnosu na sledeći prema pravilu desne ruke.

Da bi se lakše uverili o smeru okretnog efekta, jednostavno zapamtite da kada se naklanja pod uglom okretanje točkića stremi da se vrati ka unutra.

MEMS žiroskopi koriste ideju Fokaultovog klatna i koriste vibrirajući element, poznat kao MEMS(mikro elektro-mehanički sistem).

Primena[uredi | uredi izvor]

Žiroskopi se mogu koristiti za izgradnju žirokompasa koji dopunjavaju ili zamenjuju magnetske kompase (u brodovima, letelicama i vozilima u celini), kao stabilizatori (bicikli, svemirski teleskop „Habl“, brodovi, vozila u celini), ili korišćeni kao deo unutrašnjeg sistema navođenja. Neki uređaji na principu slobodnog izlaznog obruča koriste se za merenje naklona, okretanja ili skretanja odnosno uglova kretanja letelice.

Žiroskop pokazuje niz pojava, uključujući precesiju i uvrtanje.

Sisteme stabilizacije[uredi | uredi izvor]

Postoje tri osnovna vida sistema stabilizacije.

Sistema prisilne stabilizacije (na 2-stepenim žiroskopima).

Za stabilizaciju oko svake ose potreban je po jedan žiroskop. Stabilizacija se dostiže žiroskopom i stabilizacionim motorom. U početku dejstvuje žiroskopski momenat, a posle se uključuje stabilizacioni motor.

Sistema indikatorno-prisilne stabilizacije (na 2-stepenim žiroskopima).

Za stabilizaciju oko svake ose potreban je po jedan žiroskop. Stabilizacija se dostiže samo stabilizacionim motorom, ali se u početku pojavljuje manji žiroskopski momenat koji se može zanemariti.

Sistema indikatorne stabilizacije (na 3-stepenim žiroskopima).

Za stabilizaciju oko dve ose potreban je jedan žiroskop. Stabilizacija se dostiže samo stabilizacionim motorom.

Novi tipovi žiroskopa[uredi | uredi izvor]

Stalno rastući zahtevi za tačnost i eksploatacione karakteristike žiro-uređaja teraju naučnike i inženjere mnogih zemalja ne samo usavršavati klasične žiroskope sa vrtećim rotorom, nego i tražiti principalno nove ideje, koji bi mogli da reše problem stvaranja osetljivih senzora za merenje i izobraženja parametara ugaonog okretanja objekta.

Trenutno je poznato više od stotine različitih pojava i fizičkih principa, koji omogućuju rešavati žiroskopske zadatke. U Rusiji i SAD je izdato na hiljade patenata i autorskih svedočanstava za odgovarajuće izume i pronalaske.

Zbog toga što su se žiroskopi koristili u sistemima navođenja strateških raketa dejstvujućih na velikim rastojanjima za vreme Hladnog rata informacija o velikom broju istraživanja, provedenim u toj oblasti, klasifikuju se kao vojna tajna.

Perspektivnim pravcem razvića su kvantni žiroskopi.

Igračke[uredi | uredi izvor]

Žiroskopski efekti su iskorišćeni u igračkama poput čigre, jo-jo-a i pauerbolova. Mnogi drugi rotirajući uređaji, kao što su zamašnji, ponašaju se kao žiroskopi iako ne koriste žiroskopski efekat.

1917. godine, Svećarska Kompanija Indianapolisa(Indiana) napravila je „svećarski žiroskop“, žiroskopsku igračku (jo-jo) sa kanapom za zavrtavanje i postoljem. Ona je bila u neprekidnoj proizvodnji od tad i smatra se klasičnom američkom igračkom.

Perspektive razvića žiroskopije[uredi | uredi izvor]

Postojeći na današnji dan žiroskopski sistemi su toliko tačni, da mnogim potrošačima nije potrebno uveličanje tačnosti, mada je skraćivanje vojnih budžetnih sredstava kod većine vodećih svetskih zemalja, nateralo inženjere iz dane oblasti da pređu na adaptaciju žiroskopskih sistema za primenu u sferi svakodnevnih tehničkih proizvoda. Na primer, korišćenje mikromehaničkih žiroskopa za stabilizaciju kretanja automobila, video-kamera, foto-aparata, mobilnih telefona i slično.

U isto vreme progres u oblasti satelitske navigacije GPS i GLONASS, po mišljenju pristalica tog načina navigacije, učinio je nepotrebnim autonomna sredstva navigacije za slučajeve kada se satelitski signal može primati neprekidno. Kako oni kažu, radi se o tome da će trenutno građena sistema navigacionih satelita treće generacije omogućavati opredeljenje koordinata objekata na površini Zemlje sa tačnošću do nekoliko centimetara. Pritom, po njihovim rečima, otpada potreba u upotrebi čak i žiroskopa za opredeljenje kursa, jer sravnjenje podataka dva prijemnika satelitskih signala, postavljenih na rastojanju od nekoliko metara, na primer, na krilima aviona, dozvoljava izračunavati skretanje aviona po vertikalnoj osi. Takav sistem, bi ostavio bez posla desetine hiljada radnika preduzeća koja prave žiroskope za avione i brodove.

Ali, u praksi sistemi GPS nisu sposobni da tačno opredele položaj u gradskim uslovima, pri lošoj vidljivosti satelita. Takvi problemi postoje i u šumskim predelima. Čak i u avionima GPS, mada i efikasniji nego brzinometra na velikim distancama, ima veću pogrešnost kako pri merenju uglova (neki put i na cele stepene) koristeći dva GPS-prijemnika, tako i pri izračunavanju kursa putem opredeljenja brzine aviona. Zato je barem za sada najbolja varijanta za navigacione sisteme — kombinacija žiroskopskih sistema i GPS.

Uračunavajući nabrojane razloge, može se reći da je evolucija žiroskopske tehnike za poslednje decenije došla na prag važnih promena, i baš zbog toga pažnja specijalista u oblasti žiroskopije je sada usmerena na traženje nestandardnih primena takvih pribora. Otvorile su se savršeno novi interesantni zadaci. To je potraga novih korisnih iskopina, predskazivanje zemljotresa, svrhtačnih opredeljenja položaja železničkih puteva i naftovoda, medicinska tehnika i mnogo drugo.

Istorija[uredi | uredi izvor]

Najraniji poznati žiroskop izradio je Johan Bonenberger 1817. godine, mada ga je on nazvao jednostavno „Mašina“. Francuski matematičar Pjer-Simon Laplas, radeći u Politehničkoj školi u Parizu, preporučio je mašinu za korišćenje kao nastavno pomagalo, tako ju je primetio Leon Fuko.^[1] 1852. godine, Fuko ga je koristio u eksperimentu za rotaciju Zemlje i dao uređaju njegovo današnje ime. U eksperimentu se videla (Grčki skopin, videti) rotacija (Grčki giros, krug ili rotacija) Zemlje, iako je eksperiment bio neuspešan zbog trenja koje je ograničavalo svaki pokušaj na nekih 8 do 10 minuta, što je vreme prekratko za uviđanje značajnih pokreta.

1860-tih, elektromotori su omogućili koncept izvodljivim, što je dovelo do prvog prototipa žirokompasa. Prvi funkcionalni morski žirokompas napravljen je između 1905 i 1908. godine nemačkim pronalazačem Hermanom Anšutc-Kempfemom. Amerikanac Elmer Spjeri usledio je sa sopstvenim dizajnom 1910. godine, I drugi narodi su ubrzo shvatili vojnu važnost pronalaska–u doba u kojem je pomorska moć bila najznačajnija mera vojne snage–i pravili sopstvene žiroskopske industrije. Žiroskopska Kompanija Spjeri se brzo proširila da bi obezbedila avionske i brodske stabilizatore, a ostali proizvođači su ih sledili u stopu.^[2]

U prvih nekoliko decenija 20. veka, razni pronalazači pokušavali su (bezuspešno) da iskoriste žiroskop kao osnovu za prve navigacione sisteme na osnovu crnih kutija stvaranjem stabilne platforme sa kojih bi se mogla vršiti precizna merenja ubrzanja (da bi isključili potrebu za znanjem položaja zvezda za izračunavanje položaja). Slični principi su kasnije iskorišćeni u razvoju unutrašnjih sistema navođenja za balističke rakete.^[3]

Žirostat[uredi | uredi izvor]

Žirostat je varijanta žiroskopa. Prvi žirostat je projektovao lord Kelvin da ilustruje složenije stanje kretanja rotirajućeg tela dok slobodno luta na horizontalnoj ravni, kao čigra na pločniku, obruč ili bicikl na putu. Sastoji se od masivnog zamašnja skrivenog u kućištu. Njegovo ponašanje na stolu, ili uz razne oblike suspenzija ili podrški, služi za ilustraciju interesantnog obrta običnih zakona statičke ravnoteže zbog žirostatičkog ponašanja nevidljivog unutrašnjeg zamašnja dok se ovaj ubrzano okreće.

Reference[uredi | uredi izvor]

^ Wagner JF, "The Machine of Bohnenberger," The Institute of Navigation [1]
^ MacKenzie 1990, str. 31–40
^ MacKenzie 1990, str. 40–42.

Literatura[uredi | uredi izvor]

MacKenzie, Donald (1990). Inventing Accuracy: A Historical Sociology of Nuclear Missile Guidance. Cambridge: MIT Press. str. 31—40. ISBN 978-0-262-13258-9.

Dodatna literatura[uredi | uredi izvor]

Knjige

Felix Klein and Arnold Sommerfeld, "Uber die Theorie des Kreisels" (Tr., About the theory of the gyroscope). Leipzig, Berlin, B.G. Teubner, 1898-1914. 4 v. illus. 25 cm.
Audin, M. Spinning Tops: A Course on Integrable Systems. New York: Cambridge University Press, 1996.

Spoljašnje veze[uredi | uredi izvor]

Dokumenta

Theory and Design of Micromechanical Vibratory Gyroscopes, Vladislav Apostolyuk

Lekcije

The Royal Institution’s 1974–75 Christmas Lecture Professor Eric Laithwaite

[1] Wagner JF, "The Machine of Bohnenberger," The Institute of Navigation [1]

[2] MacKenzie 1990, str. 31–40

[FOOTNOTEMacKenzie199040–42-3] MacKenzie 1990, str. 40–42.

[1]

[2]

[3]

Normativna kontrola
Državne	Francuska BnF podaci Nemačka Izrael Sjedinjene Države Japan Češka
Ostale	Enciklopedija Britanika