Пејзаж фрактала

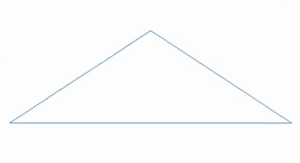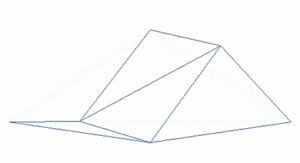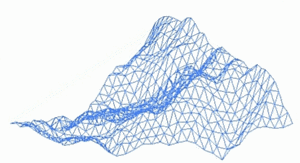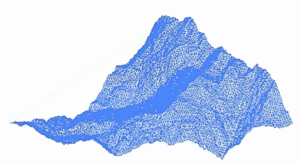
 Фрактал пејзаж је површина генерисана коришћењем стохастичког алгоритма дизајнирана да произведе фрактално понашање које имитира изглед природног терена . Другим речима, резултат поступка није детерминистички фрактал површина, већ случајна површина која показује фрактално понашање.

 Многи природни феномен испољавају неку врсту статистичке самосличности које се могу осмислити фракталним површинама . Штавише, варијације у површинској текстури дају важне визуелне знаке за оријентацију и обронцима површина , као и коришћење скоро само- сличан фракталних образаца може помоћи у стварању природног изгледа визуелних ефеката. Моделирање Земљине површине преко фракционог Брауновог кретања је први предложио Беноа Манделброт.

Зато што је жељени резултат овог процеса је да се произведе пејзаж, а не математичка функција , процеси се често примењују на такве пејзаже коие могу утицати на стационарност , па чак и укупно фрактално понашање такве површине , у интересу производећи уверљивији пејзаж .

Према РР Шеарер , генерација природног изгледа површина и пејзажа је била главна прекретница у историји уметности , где је разлика између геометријске , генерисане компјутерске слике и природне , човек је направио уметност, постала замагљена.Прва употреба фракталног генерисаног пејзажа у филму је у 1982. за филм Звездане стазе II: Канов гнев.Лорен Карпентер рафинирао је технику Манделброт да створи ванземаљаски пејзаж.

Понашање пејзажа природе

Пример компјутерско генерисаног фрактала пејзажа

Компјутерски генерисан фрактал терена

Компјутерски генерисан фрактал шумовитх брда

Без обзира да ли се природни пејзажи понашају на начин који је генерални фрактални, био је предмет неким истраживањима. Технички гледано, свака површина у тродимензионалном простору има тополошку димензију 2, и стога сваки фрактал површина у тродимензионалном простору има Хаусдорфову димензију између 2 и 3. Реални пејзажи, међутим, имају различито понашање у различитим размерама. То значи да је покушај да се израчуна укупан „Фрактал димензија стварног пејзажа може да доведе до мере негативне фракталне димензије, или фракталне димензије изнад 3. Посебно многим студијама природног феномена, чак и они обично се сматра да испољавају понашање фрактал , не у ствари, тако да је преко више од неколико редова величине. На пример, испитивање Рихардове западне обале Британије показала фракталног понашање обале над само два реда величине. У принципу, нема разлога да се претпостави да су геолошки процеси који обликују терен на великим скалама (на пример плоча тектонике) показују исто математичко понашање и оних који облик терена на мањим размерама (за пример смицање земљишта). 

Реални пејзажи такође имају различита статистичка понашања од места до места , тако да на пример пешчане плаже не показују исте особине као и фракталне планинских венаца . Фрактал функција је , међутим, статистички стационарни , што значи да њени булк статистичких особина је свуда исти . Према томе, свако прави приступ моделовању пејзажа захтева способност да модулирају фрактално понашање просторно . Осим тога прави пејзажи имају врло мало природног минимума ( већина њих су језера ) , док је фрактал функција има онолико минимума као максимума , у просеку . Реални пејзажи имају карактеристике које потичу са протоком воде и леда преко њихове површине , што једноставни фрактали не могу моделирати.  

То је због ових разматрања да су једноставне фрактал функције често неприкладне за моделирање пејзажа . Више софистициране технике ( познате као ' ' Мултифрактал" техника ) користе различите фракталне димензије за различите скале , и на тај начин могу боље модел понашања фреквенцијског спектра реалних предела

Производња фракталног пејзажа

Један од начина да се направи такав пејзаж је да запосли случајно средиште расељавања алгоритама , у којој је квадрат подељен на четири мања једнака квадрата и централна тачка је вертикално изабрана неким случајним износ. Поступак се понавља на четири нова квадрата , и тако даље, све док се не достигне жељени ниво детаља . Постоје многе фракталне процедуре ( као што комбинује више октава Симплек буке ) способне за креирање података терена , међутим , термин " фрактал пејзаж " је постао генерички . 

Види још

• Браунова површина
• Брице
• Дијамант-квадратни алгоритам
• Гром
• Оутера
• Тетраген
• Октално стабло
• Квадратно стабло

Литература

• Briggs, John (1992). Fractals: The Patterns of Chaos : a New Aesthetic of Art, Science, and Nature. Simon and Schuster. стр. 84. ISBN 978-0-671-74217-1. Приступљено 15. 6. 2014. 
• Rhonda Roland Shearer (2002). Galaburda Albert M.; Kosslyn Stephen Michael, ур. The Languages of the Brain; Rethinking Images and Metaphors. Harvard University Press. стр. 356. ISBN 978-0-674-00772-7. 
• Cham, Tat-Jen; Cai, Jianfei; Dorai, Chitra; Rajan, Deepu; Tat-Seng Chua; Liang-Tien Chia (22. 12. 2006). Advances in Multimedia Modeling: 13th International Multimedia Modeling Conference, MMM 2007, Singapore, January 9-12, 2007, Proceedings. Springer Science & Business Media. стр. 297. ISBN 978-3-540-69428-1. 
• Lewis, J.P. „Is the Fractal Model Appropriate for Terrain?” (PDF). 
• Richardson, L.F. (1961). „The Problem of Continuity”. General Systems Yearbook. 6: 139—187. 
• van Lawick van Pabst, Joost; Jense, Hans (2001). „Dynamic Terrain Generation Based on Multifractal Techniques” (PDF). Архивирано из оригинала (PDF) 24. 07. 2011. г. Приступљено 28. 11. 2015. 
• Musgrave, Ken (1993). „Methods for Realistic Landscape Imaging” (PDF). 

Спољашње везе

• 3D Fractal Mountains in Java
• MDTerrain Terrain Generator using Midpoint Displacement
• A Web-Wide World by Ken Perlin, 1998; a Java applet showing a sphere with a generated landscape.