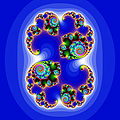
Фрактал


Фрактал је „геометријски лик који се може разложити на мање делове тако да је сваки од њих, макар приближно, умањена копија целине“.[1] Још се каже да је такав лик сам себи сличан. Термин је извео Беноа Манделброт 1975.[2] године из латинске речи fractus која има значење „сломљен“, „разломљен“.
Фрактал често има следеће особине:[3][4]
- фину структуру на произвољно малом увећању;
- превише је неправилан да би могао бити описан традиционалним еуклидским језиком;
- сам је себи сличан (макар приближно или стохастично);
- Хауздорфову димензију која је већа од његове тополошке димензије (иако овај услов не испуњавају бесконачно густе криве као што је Хилбертова крива);[5][6]
- једноставну и рекурзивну дефиницију.
Пошто се чине сличним на свим нивоима увећања, фрактали се често сматрају бесконачно комплексним у неформалном смислу речи. Природни облици који апроксимирају фрактале до извесне границе су облаци, планински венци, муње, морске обале, и снежне пахуљице. Међутим, нису сви објекти који су сами себи слични истовремено и фрактали – пример је реална права која је формално сама себи слична, али не поседује остале особине фрактала.
Историја[уреди | уреди извор]

Математика која се налази у основи фрактала почела је да поприма свој облик у 17. веку када је математичар и филозоф Лајбниц разматрао особину рекурзивне сличности самом себи, иако је он, грешком, сматрао да је само права линија слична самој себи у том смислу. Тек 1872. године појављује се прва функција чији бисмо график данас сматрали фракталом, када је Карл Вајерштрас дефинисао функцију која је имала неинтуитивну особину да је на целој области дефинисаности била непрекидна, али да ни у једној тачки није била диференцијабилна. Три деценије касније, 1904. године Хелг Кох, незадовољан Вајерштрасовом превише апстрактном и аналитичком дефиницијом, у свом раду О једној непрекидној кривој без тангенти, добијеној помоћу елементарне геометријске конструкције (Sur une courbe continue sans tangente, obtenue par une construction geometrique elementaire) објављеном у часопису Arkivfor Matematik[7][8] даје геометријски дефиницију криве која је данас позната као Кохова пахуљица. 1915. године Вацлав Сјерпињски је конструисао свој троугао, а годину дана касније и тепих Сјерпињског. У оригиналу, сви ти геометријски фрактали су били описани као криве, а не као дводимензионални облици, како се третирају у модерним дефиницијама. Идеју о кривама које су сличне саме себи је даље развио Пол Пјер Леви, који је 1938. године у свом раду Раванске или просторне криве и површи које су састављене од делова сличних целини (Plane or Space Curves and Surfaces Consisting of Parts Similar to the Whole) описао нову фракталну криву, познату данас као Левијева Ц крива.
И Георг Кантор је, у периоду 1879—1884, када је објављивао серију од шест чланака који су заједно били увод у његову теорију скупова, разматрао примере подскупова реалне праве са неуобичајеним особинама. Ти Канторови скупови су данас сврстани у фрактале.
Пред крај 19. и почетком 20. века Анри Поенкаре, Феликс Клајн, Пјер Фату и Гастон Жулија су истраживали итерирајуће функције у комплексној равни. Међутим без помоћи графике савремених рачунара, нису имали могућност визуелизације лепоте већине објеката које су открили.
Беноа Манделброт је шездесетих година 20. века почео да се бави самосличношћу у својим радовима као што је чланак Колико је дугачка британска обала? Статистичка самосличност и разломљене димезије (How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension), заснован на једном ранијем делу које је објавио Луис Фрај Ричардсон.
Напокон, 1975. године, Манделброт је употребио реч „фрактал“ да њоме означи објекат који је имао особину да му је Хауздорфова димензија већа од тополошке. Ту математичку дефиницију је илустровао задивљујућом визуелизацијом добијеном помоћу рачунара. Већина генерисаних слика била је заснована на рекурзији, и тиме одредила општеприхваћено значење речи „фрактал“.
Области појављивања и примене фрактала[уреди | уреди извор]
Фрактали се често појављују као атрактори динамичких система, чак и у ситуацијама које се чине прилично једноставним (нпр. Жулијин скуп). У компјутерској графици, фрактали се користе за генерисање слика које представљају природне објекте[9]: облаке, снег, морске обале, планинске венце, хрпе отпада...
Класификација фрактала[уреди | уреди извор]
Према основној подели разликују се
- геометријски,
- алгебарски и
- стохастични фрактали.
Поред тога, фрактали се, према постанку, могу поделити на природне и вештачке, где се под вештачким фракталима подразумевају они до којих су дошли научници, а који, при произвољном увећању, задржавају особине фрактала. Код природних фрактала се јавља ограниченост области егзистенције - постоје максимална и минимална величина размере објекта за коју он поседује фракталне особине.
 |
 |
 |
 |
| Полазни Манделбротов скуп | Увећање шест пута | Увећање 100 пута | Фини детаљи подсећају на полазни скуп |
Фрактали се још деле на
- детерминисане (овде спадају геометријски и алгебарски фрактали) и
- недетерминисане (стохастичне фрактале).
У односу на степен самосличности, фрактали могу бити:
- потпуно самослични - највећи степен самосличности. Фрактал је идентичан самом себи на произвољном нивоу увећања. Ову особину имају фрактали кој се добијају помоћу итеративних функција.
- скоро самослични - мање строг облик самосличности; фрактал делује приближно (али не и потпуно) идентичан самом себи на различитим нивоима увећања. Овакве фрактале чине умањене копије целог фрактала у изобличеним и дегенерисаним облицима. Обично су то фрактали који се добијају помоћу рекурентних веза.
- статистички самослични - најнижи ниво самосличности. Фрактал поседује нумеричке или статистичке мере које се чувају кроз увећање или умањење. Најједноставније дефиниције фрактала тривијално указују на неку врсту статистичке самосличности (фрактална димензија је сама по себи нумеричка величина која се не мења са увећањем, односно умањењем). Овде спадају фрактали генерисани стохастичким процесима.
Геометријски фрактали[уреди | уреди извор]


Геометријски фрактали су први фрактали које су изучавали математичари у 19. веку, захваљујући њиховој очигледности, односно зато што је код њих одмах приметна особина самосличности.
Дводимензионе геометријске фрактале је могуће добити задавањем произвољне криве која ће послужити као генератор. Затим се, у сваком следећем кораку, средњи део те криве замени генератором - умањеним ликом целе криве. Бесконачним понављањем овог поступка добија се изломљена фрактална крива. Иако је та крива веома сложена, њен општи облик могуће је задати само генератором. На тај начин могу се генерисати змајева крива, Кохова крива, Левијева крива, крива Минковског, Пеанова крива и Хилбертова крива.
Поред наведених фракталних кривих, у геометријске фрактале спадају и Канторов скуп, као и његова вишедимензиона уопштења, Канторова прашина (у равни) и Канторов облак (у простору), троугао Сјерпињског, тепих Сјерпињског, Питагорино дрво и Менгеров сунђер.
Бесконачно густе криве[уреди | уреди извор]
Бесконачно густе криве су фракталне криве које након бесконачног броја итерација потпуно прекривају део -димензионог простора у којем се налазе (). Тако ће бесконачно густа крива у равни заузимати сваку тачку нпр. квадрата, а у тродимензионом простору сваку тачку коцке. Први их је описао италијански математичар Ђузепе Пеано, па се све оне понекад називају Пеановим кривама.
Својства[уреди | уреди извор]
Фракталне димензије свих бесконачно густих кривих одговарају тополошкој димензији простора у којем се налазе, баш зато што испуњавају читав тај простор, иако је њихова тополошка димензија увек . Дакле, фрактална димензија бесконачно густих кривих у равни (јединичном квадрату) је , у простору (јединичној коцки) је итд.
Пеанова крива[уреди | уреди извор]
Пеанова крива је прва описана бесконачно густа крива. Њу је 1890. године описао италијански математичар Ђузепе Пеано.[10]
Конструкција[уреди | уреди извор]
Пеанова крива се конструише низом итерација. Прва итерација је задата каква јесте. Наредну итерацију добијамо на следећи начин:
- Претходну итерацију посматрамо као квадрат и поделимо га на 9 нових квадрата једнаких величина.
- Сваки од тих квадрата заменимо 9 пута умањеним квадратом из претходне итерације.
- Затим се изврши хоризонтална, односно вертикална рефлексија квадрата, како би спајање било коректно извршено.
- На крају, криве у квадратима се споје у једну непрекидну криву.
 |
| Прве три итерације Пеанове криве |
Постоји велики број варијанти Пеанових кривих, у зависности изгледа прве итерације и поделе на квадрате.
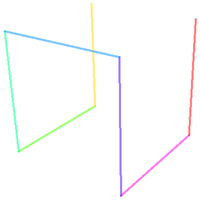
Хилбертова крива[уреди | уреди извор]

При конструкцији Хилбертове криве користи се идеја базирана на подели квадрата на 4 мања, уместо на 9 мањих квадрата једнаких величина.
Хилбертова крива је бесконачно густа крива коју је описао немачки математичар Давид Хилберт 1891.[11] године.
Хауздорфова димензија Хилбертове криве је . Иако је Хилбертова крива у равни ограничена квадратом, њена дужина експоненцијално расте са бројем итерација и износи .
Конструкција[уреди | уреди извор]
Конструкција је слична конструкцији Пеанове криве. Прво, задају се две почетне итерације (онакве какве јесу), а затим се у свакој наредној итерацији сви сегменти слични кривој из прве итерације замене читавом кривом из друге итерације. Даља конструкција се може извршити на два начина, иако је резултат потпуно исти:
- -ту итерацију добијемо ако у -ој итерацији сваки сегмент сличан кривој из прве итерације заменимо читавом другом итерацијом.
- -ту итерацију добијемо ако у -ој итерацији сваки сегмент сличан кривој из претходне итерације заменимо том читавом итерацијом.
 |
 |
 |
| Прва итерација | Прва и друга итерација | Прве три итерације |
Хилбертова крива у простору се прави једноставном аналогијом.
 |
 |
 |
 |
||||||||||||||||
| Прва итерација | Друга итерација | Трећа итерација | Четврта итерација |
Конструкција коришћењем L-система[уреди | уреди извор]
- Почетак:
- Правила:
- →
- →
- Значење:
- "цртај напред"
- "окрени у смеру казаљке на сату за "
- "окрени у смеру супротном од смера казаљке на сату за "
Примене[уреди | уреди извор]
Хилбертова крива има вишеструке примене у разним областима, а највише у рачунарству и информатици. Користи се код IP адреса рачунара, како би могла да се конструише слика мреже. Код за генерисање слике ће претворити 2D у 1D да би нашао боју сваког пиксела, а Хилбертова крива се понекад користи јер блиске IP адресе у слици чува једну близу друге. Такође је нашла примену у мултидимензионим базама података - при тражењу записа могу помоћи у одређивању приоритета претраге. Користе се и при изради црно-белих фотографија. Хилбертове криве у већим димензијама представљају генерализацију Грејевог кода, и користе се у сличне сврхе.
Алгебарски фрактали[уреди | уреди извор]
Алгебарски фрактали су они фрактали за чију се конструкцију користе итеративне нелинеарне функцијекоје се задају једноставним алгебарским формулама.

У 16. веку италијански математичари су развили егзактне формуле за решавање алгебарских једначина трећег и четвртог степена, а почетком 19. века математичар Нилс Абел доказао је да не постоје универзалне методе којима би се решавале једначине петог и вишег степена. Но, такве се једначине могу решавати приближно, до потребне тачности. Методе приближног решавања једначина развијале су се током више векова. Исак Њутн је развио специифчну итеративну методу коју је касније усавршио Џозеф Рафсон.
Претпоставимо да нула непрекидне функције припада интервалу . Одаберемо једну од крајњих тачака интервала, на пример , и одредимо тангенту у њој. Означимо тачку пресека тангенте и апсцисе и поступак поновимо примењен на интервал . Поступак поноваљамо све док не постигнемо задовољавајућу тачност решења, односно док посматрани интервал не постане довољно мали.
Треба приметити да у случајевима са слика са стране приближна решења постају све ближа стварном решењу, односно конвергирају му, иако су код леве функције "суседна" приближна решења увек са супротне стране стварног.
Ова метода може се применити и на комплексну раван. Размотримо нуле комплексне функције .
Из графика са стране видимо да су границе три скупа сложене те да даљим повећавањем добијамо све већу сложеност. Осим тога, гранична подручја садрже подручја која су потпуно слична подручјима у којима се налазе. Другим речима, она поседују својство самосличности, односно то су фрактали.
Жулијин скуп[уреди | уреди извор]

Жулијин скуп (у ширем смислу) је граница скупова тачака у којима низ конвергира и скупа тачака за које тај низ дивергира. Овде може бити било kоја функција.
Жулијин скуп (у ужем смислу) добијамо ако за функцију изаберемо .
Добио је име по француском математичару Гастону Жулији[12].
Конструкција[уреди | уреди извор]
Ако се за сваку тачку комплексне равни дефинише низ , где је може бити било која функција, можемо дефинисати два скупа:скуп тачака за које дефинисани низ конвергира и скуп тачака за које тај низ дивергира, односно тежи у бесконачност[13]. Жулијин скуп (у ширем смислу) је граница тих скупова. Обично се Жулијин скуп, као и сви алгебраски фрактали, приказује тако да су тачке које конвергирају црне, а оне које дивергирају у разним нијансама исте или различитих боја . Нијанса боје зависи од брзине којом низ расте – што се више одмичемо од Жулијиног скупа, низ брже расте. Мењањем константе у Жулијином скупу у ужем смислу добијамо најразличитије скупове[14].
Повезаност[уреди | уреди извор]
Жулијин скуп је повезан ако је скуп који окружује компактан.[13]. Ова је особина врло важна за дефиницију Манделбротовог скупа.
-
c=1-φ, φ = zlatni rez
(повезан) -
c=(φ-2)+(φ-1)i = -0.4+0.6i
(неповезан) -
c=0.285+0i
(неповезан) -
c=0.285+0.01i
(неповезан) -
c=0.45+0.1428i
(неповезан) -
c=-0.70176-0.3842i
(повезан)
Манделбротов скуп[уреди | уреди извор]
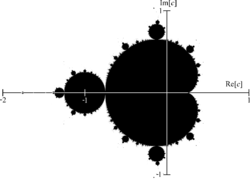
Манделбротов скуп је најсавршенији од свих фрактала. Одређен је рекурентном функцијом , где је комплексан број такав да је Жулијин скуп повезан.
Тачније, Манделбротов скуп је скуп свих комплексних бројева таквих да је, за почетни услов , модуо комплексног броја ограничен.
Све тачке Манделбротовог скупа леже унутар круга полупречника 2. Наиме:
.
Разни самослични фрактали, којима припада и Манделбротов, најједноставније се конструишу уз помоћ "escape - time" алгоритма.
Псеудо код за цртање Манделбротовог скупа:
ulaz: sirina i visina ekrana;
maksimalni broj iteracija max_iter;
niz[];
begin
for i := 0 to visina do
for j := 0 to sirina do
Re_c = (j - sirina / 2) * 4 / sirina;
Im_c = (i - visina / 2) * 4 / sirina;
x = 0; y = 0;
iter = 0;
while x * x + y * y <= 4 and iter < max_iter do
tmp = x * x - y * y + Re_c;
y = 2 * x * y + Im_c;
x = tmp;
iter++;
if iter < max_iter then
oboji_piksel(j, i, boja[iter]);
else
oboji_piksel(j, i, crno);
end
Горући брод[уреди | уреди извор]
Горући брод је фрактал којег су описали Мајкл Микетлиш и Ото Рослер 1992. Конструише се на сличан начин као и Жулијин скуп: за сваку тачку комплексне равни одреди низ тачака tako da je и . Тачке које након много итерација конвергирају ка једној вредности припадају скупу, па се обоје једном бојом. Остале тачке дивергирају и обоје се различитим нијансама, зависно од тога колико брзо дивергирају.


Њутнов фрактал[уреди | уреди извор]

Њутнова метода за налажење корена функције се базира на, такође, итеративном процесу. Њутнов фрактал је управо граница скупа у комплексној равни дефинисаног Њутновим методом примењеним на полином комплексног броја. Са Манделбротовим скупом, Њутнов метод је повезан на најневероватнији начин. Испитиван је Њутнов метод над одређеном кубном комплексном функцијом. На комплексној равни са три боје су обележаване тачке које би као почетне довеле до откривања корена једнаком , тачке које би конвергирале ка неком од преостала два корена и тачке које су упадале у циклусе између бар два корена. Увеличавањем добијене слике откривен је фрактал Манделбротовог скупа, онако како га знамо за квадратну итеративну функцију, а припадао је области тачака које нису конвергирале ка само једном корену.
За неке веома једноставне физичке системе (механички, магнетни, оптички, итд.) показује се да су атракторске области коренова изразито фрактално разломљене и једноставни системи постају практично непредвидљиви. Њихово коначно стање драстично зависи од почетних услова и ово је прва назнака повезаности фрактала и хаоса.
Види још[уреди | уреди извор]
Референце[уреди | уреди извор]
- ^ Mandelbrot 1982.
- ^ Edgar, Gerald (2008). Measure, Topology, and Fractal Geometry. New York: Springer Science+Business Media. стр. VII. ISBN 978-0-387-74748-4.
- ^ Falconer, Fractal Geometry: Mathematical Foundations and Applications}-, стр. -{xxv
- ^ Falconer 1982.
- ^ Briggs 1992, стр. 148
- ^ The Hilbert curve map is not a homeomorhpism, so it does not preserve topological dimension. The topological dimension and Hausdorff dimension of the image of the Hilbert map in R2 are both 2. Note, however, that the topological dimension of the graph of the Hilbert map (a set in R3) is 1.
- ^ Novak, Thinking in Patterns: Fractals and Related Phenomena in Nature. стр. 177.
- ^ Miroslav M. Novak, ур. (2004). Thinking in Patterns: Fractals and Related Phenomena in Nature. World Scientific Publishing Co. Pte. Ltd. ISBN 978-981-238-822-3.
- ^ "Hunting the Hidden Dimension." Nova. PBS. WPMB-Maryland. 28 October 2008.
- ^ Peano, G. (1890), „Sur une courbe, qui remplit toute une aire plane”, Mathematische Annalen, 36 (1): 157—160, doi:10.1007/BF01199438
- ^ D. Hilbert: Über die stetige Abbildung einer Linie auf ein Flächenstück. Mathematische Annalen 38 (1891), 459—460.
- ^ Gaston Julia (1918) "Mémoire sur l'iteration des fonctions rationnelles," Journal de Mathématiques Pures et Appliquées, vol. 8, pages 47—245.
- ^ а б Beardon, Iteration of Rational Functions, Theorem 5.6.2
- ^ Peitgen & Richter 1986
Литература[уреди | уреди извор]
- Peitgen, Heinz-Otto; Richter, Peter (1986). The Beauty of Fractals. Heidelberg: Springer-Verlag. ISBN 978-0-387-15851-8.
- Mandelbrot, B.B. (1982). The Fractal Geometry of Nature. W.H. Freeman and Company. ISBN 978-0-7167-1186-5.
- Edgar, Gerald (2008). Measure, Topology, and Fractal Geometry. New York: Springer Science+Business Media. стр. VII. ISBN 978-0-387-74748-4.
- Falconer, Kenneth (1982). Fractal Geometry: Mathematical Foundations and Applications. John Wiley & Sons, Ltd. ISBN 978-0-470-84862-3.
- Miroslav M. Novak, ур. (2004). Thinking in Patterns: Fractals and Related Phenomena in Nature. World Scientific Publishing Co. Pte. Ltd. ISBN 978-981-238-822-3.
Спољашње везе[уреди | уреди извор]
- Фрактали на mathworld.wolfram.com (језик: енглески)
- Предавања о фракталима са Универзитета Јејл (језик: енглески)
- Хаос и фрактали (језик: енглески)
- Особине фрактала (језик: енглески)
- Фрактали - чудесне слике хаоса (језик: хрватски)
- Фрактални облици у нумеричким апроксимацијама (језик: хрватски)





















![{\displaystyle [A,B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1993067bb075f2ebfa02e78959b7c5bed68e06f4)


![{\displaystyle [A',B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e2e6643d1f6afc99a8c4040e7b4f97f290f2321)