Магични квадрат (слагалица)
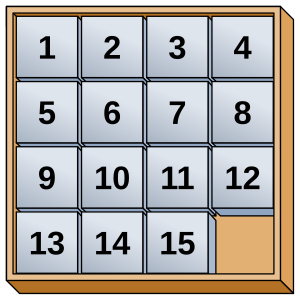
Магични квадрат (енгл. Gem Puzzle, Boss Puzzle, Game of Fifteen, Mystic Square) је клизна слагалица која се састоји од рама у којем се налазе квадратне плочице поређане по случајном редоследу при чему једна плочица недостаје. Ова слагалица постоји и у другим величинама, попут мање "игре 8 пазли". Ако је однос плочица 3x3, онда се зове "игра 8 пазли" или "игра 9 пазли", а ако има однос плочица 4x4, онда је то "игра 15 пазли" или "игра 16 пазли".
Циљ слагалице је поређати плочице по растућем поретку (као што је приказано на слици), клизним померањем једне по једне плочице на празан простор. Ова игра представља класичан проблем моделовања алгоритма који користи хеуристику. Најчешће коришћена хеуристика за овај проблем укључује бројање погрешно постављених плочица и проналажење растојања између сваког блока и његовог циљног положаја.
Решивост[уреди | уреди извор]
Џонсон и Стори су 1879. године искористили аргумент паритета да покажу да је половину почетних конфигурација немогуће решити, без обзира колико потеза је направљено. Дошли су до овог закључка посматрајући функциију конфигурација плочица која је непроменљива након било ког потеза, и затим искористили ово да поделе простор свих могућих обележених стања у две еквивалентне класе могућих и немогућих стања.
Инваријанта представља збир паритета пермутација свих 16 плочица и паритета разлике између збира колона плус збира редова и празне плочице у доњем десном углу. Непроменљива је јер сваки покрет мења паритет пермутација и паритет разлике. Конкретно, ако је празна плочица у доњем десном углу а број пермутација је паран, слагалица је решива.

Вилсон је 1974. године проучавао аналогију између игре 15 пазли и произвољних коначних повезаних и нераздвојивих графова. Граф се сматра раздвојивим уколико уклањањем једног чвора повећавамо број компонената. Показао је, осим за полигоне и један посебни граф са седам чворова, да је могуће добити све пермутације осим ако је граф бипартитиван, и у том случају само парне пермутације могу бити добијене. Посебни граф са седам чворова је регуларни хексагон са једном дијагоналом и чвором додатим у центру. Само једна шестина пермутација може бити добијена.
За веће верзије ове пазле, проналажење решења је једноставно, али проблем налажења најкраћег решења је полиномијалне комплексности. За случај са 15 плочица, дужине распона оптималних решења иду од 0 до 80 померања једне плочице, или 43 померања више плочица. Пазла са 8 плочица може бити решена у не више од 31 померања једне плочице или 24 померања више плочица.[1][2] For the 15-puzzle, lengths of optimal solutions range from 0 to 80 single-tile moves[3] Број могућих почетних конфигурација за пазле са 24 плочице је 25!/2, што је превише да би се одредио божји алгоритам, као и божји број. Доња граница је одређена 2011. године и износи 152 померања једне плочице,[4] а горња граница 208 померања једне плочице или 109 померања више плочица.[5][6] Симетрије 15 пазле формирају групоид (grupoid).[7][8]
Алтернативни доказ[уреди | уреди извор]
У алтернативном погледу проблема, можемо размотрити да је инваријанта збир паритета броја инверзија у тренутном поретку 15 нумерисаних плочица и паритета размака између броја реда празне плочице и броја реда последњег реда. Ово је непроменљиво јер свако померање у оквиру исте колоне мења и број паритета броја инверзија (мењањем броја инверзија за ±1, ±3...) и паритет размака од последњег реда (±1). Свако померање у оквиру истог реда не мења паритет. Ако погледамо решено стање загонетке, збир је паран. Самим тим, индукцијом је лако доказати да било које стање пазле у ком је збир непаран не може бити решено. Конкретно, ако је празна плочица у доњем десном углу или чак било где у последњем реду, пазла се може решити ако и само ако је број инверзија плочица са бројем паран.
Историја[уреди | уреди извор]

Загонетку је измислио Нојс Палмер Чапман, који је 1874. године у Канастоти, у Њујорку пријатељима показао пазлу која се састојала од 16 плочица обележених бројевима, које треба да се поређају заједно у редовима по четири, при чему сваки ред даје збир до 34. Копије ове пазле стигле су преко његовог сина до Сиракузе у Њујорку, а одатле до Хартфорда, Конектикат, где су ученици Америчке школе за глуве особе почели да их праве, и већ у децембру 1879. године продавали су их локално и у Бостону, Масачусетс. Матијас Рајс, власник продавнице дрвених предмета у Бостону, заинтересовао се за ову загонетку и сам је почео да их прави. У јануару 1880. године, др Чарлс Пиви, зубар из Масачусетса, привукао је пажњу понудивши новац оном ко може да је реши. Чапман је патентирао ову игру 1880. године. Исте године игра је постала популарна у Сједињеним државама, Канади, Европи, а у Јапану тек 1889. године.[9]
Сем Лојд[уреди | уреди извор]

Сем Лојду се приписује настанак слагалице, поготово јер је тврдио да је он у ствари направио ову игру, и од 1891. године до краја живота је покушавао да патентира проналазак. Те је то и написано у енциклопедији пазли (Cyclopedia of Puzzles) објављеној 1914. године:
Старији становници Пазлеленда ће памтити како сам током раних седамдесетих заинтригирао цео свет малом кутијом са помералицама које су касније постале познате као 14-15 пазле.
Међутим, Лојд није ни у ком случају био повезан са иницијалном популарношћу слагалица, јер је помама за слагалицама почела 1880их, а не раних 1870их. Лојдов први чланак о пазлама је био објављен 1886. да би се тек 1891. године он први пут почео представљати као изумитељ слагалица.[9][10]
Лојд је касније привукао додатну пажњу тако што је понудио 1000 долара свакоме ко би могао да понуди решење „Лојдове комбинације“, и да замени плочице 14 и 15 које у старту леже на замењеним позицијама. Ово је било немогуће, што су деценију раније доказали Џонсон и Стори, с обзиром да се заменом плочица десила трансформација из парне у непарну комбинацију.
Види још[уреди | уреди извор]
Референце[уреди | уреди извор]
- ^ Daniel Ratner, Manfred K. Warmuth. Finding a Shortest Solution for the N × N Extension of the 15-PUZZLE Is Intractable. National Conference on Artificial Intelligence, 1986.
- ^ Ratner, Daniel; Warmuth, Manfred (1990). „The (n²−1)-puzzle and related relocation problems”. Journal of Symbolic Computation. 10 (2): 111—137. doi:10.1016/S0747-7171(08)80001-6.
- ^ A. Brüngger, A. Marzetta, K. Fukuda and J. Nievergelt, The parallel search bench ZRAM and its applications, Annals of Operations Research 90 (1999). стр. 45–63.
- ^ "24 puzzle new lower bound: 152". Domain of the Cube Forum
- ^ "5x5 can be solved in 109 MTM". Domain of the Cube Forum.
- ^ "m × n puzzle (current state of the art)" Архивирано на сајту Wayback Machine (7. март 2016). Sliding Tile Puzzle Corner.
- ^ The 15-puzzle groupoid (1), Never Ending Books
- ^ The 15-puzzle groupoid (2), Never Ending Books
- ^ а б The 15 Puzzle, by Jerry Slocum & Dic Sonneveld. 2006. ISBN 978-1-890980-15-3.
- ^ Clarke 1994, стр. 10–12
Литература[уреди | уреди извор]
- Clarke, Barry R. (1994). Puzzles for Pleasure. Cambridge University Press. ISBN 978-0-521-46634-9.
