Правило судњег дана

Правило судњег дана или алгоритам судњег дана је начин на који може да се израчуна дан недеље према задатом датуму. Он ради са перпетуалним календаром јер се Грегоријански календар понавља на сваких 400 година.

Овај алгоритам који се служи менталним рачунањем осмислио је Џон Конвеј^[1]^[2] добивши инспирацију након што је прочитао рад Луиса Керола^[3]^[4] о вечитом календару. Алгоритам користи чињеницу да сваке године постоји дан у недељи (тзв. судњи дан) на који „падају“ одређени датуми што се лако памте, на пример 4.4. 6.6. 8.8. 10.10. 12.12. и последњи дан фебруара увек падају на исти дан у било којој години. Примена овог алгоритма састоји се из три корака:

Одредити „усидрен дан“ века
Користи тај дан да се израчуна судња година
Изабери најближи датум од оних који се лако памте (4.4. 6.6. 8.8. 10.10. 12.12.), и изброј дане по модулу 7 између тог датума и датума за који се питамо на који дан недеље пада.

Ова техника може се применити и на Грегоријански календар нове ере или Јулијански календар, иако ће њихови судњи дани понекад бити различити дани године.

Пошто овај алгоритам гледа на дане као бројеве по модулу 7, Џон Конвеј је предложио се дани недеље зову (на енглеском) "Noneday" или "Sansday" (за недељу), "Oneday", "Twosday", "Treblesday", "Foursday", "Fiveday", и "Six-a-day". Постоји неколико језика као нпр. португалски или галицијски који заснивају неке називе за дане на њиховој позицији у седмици.

Алгоритам је једноставан и не подразумева велико предзнање аритметике да би могао да се користи за ментално рачунање. Конвеј је могао да одреди дан у седмици за задати датум за мање од две секунде. Да би побољшао своју брзину, вежбао је одређивање дана у седмици на свом рачунару, који је био испрограмиран да га пита за насумичне датуме сваки пут када се укључи.^[5]

Судњи дан за неке године

Судњи дан за тренутну годину у грегоријанском календару је понедељак за 2016. годину.

За неке друге године је:

**Судњи дани за Грегоријански календар**
Пон.	Уто.	Сре.	Чет.	Пет.	Суб.	Нед.	Пон.	Уто.	Сре.	Чет.	Пет.	Суб.	Нед.
1898	1899	1900	1901	1902	1903	→	1904	1905	1906	1907	→	1908	1909
1910	1911	→	1912	1913	1914	1915	→	1916	1917	1918	1919	→	1920
1921	1922	1923	→	1924	1925	1926	1927	→	1928	1929	1930	1931	→
1932	1933	1934	1935	→	1936	1937	1938	1939	→	1940	1941	1942	1943
→	1944	1945	1946	1947	→	1948	1949	1950	1951	→	1952	1953	1954
1955	→	1956	1957	1958	1959	→	1960	1961	1962	1963	→	1964	1965
1966	1967	→	1968	1969	1970	1971	→	1972	1973	1974	1975	→	1976
1977	1978	1979	→	1980	1981	1982	1983	→	1984	1985	1986	1987	→
1988	1989	1990	1991	→	1992	1993	1994	1995	→	1996	1997	1998	1999
→	2000	2001	2002	2003	→	2004	2005	2006	2007	→	2008	2009	2010
2011	→	2012	2013	2014	2015	→	2016	2017	2018	2019	→	2020	2021
2022	2023	→	2024	2025	2026	2027	→	2028	2029	2030	2031	→	2032
2033	2034	2035	→	2036	2037	2038	2039	→	2040	2041	2042	2043	→
2044	2045	2046	2047	→	2048	2049	2050	2051	→	2052	2053	2054	2055
→	2056	2057	2058	2059	→	2060	2061	2062	2063	→	2064	2065	2066
2067	→	2068	2069	2070	2071	→	2072	2073	2074	2075	→	2076	2077
2078	2079	→	2080	2081	2082	2083	→	2084	2085	2086	2087	→	2088
2089	2090	2091	→	2092	2093	2094	2095	→	2096	2097	2098	2099	2100

Напомена: Поља се пуне хоризонтално, прескачући свако колону за сваку преступну годину. Ова табела има циклус од 28 година, сем у Грегоријанском календару када су године дељиве са 100 које нису дељиве са 400. Цео циклус траје 28 година (1, 461 недеља) у Јулијанском календару, а 400 година (20, 871 недеља) у Грегоријанском.

Битни датуми који увек падају на судњи дан

Могуће је наћи дан недеље задате календарске године помоћу блиског судњег дана као референтне тачке. Да би се то олакшало, следи листа датума који се лако памте за сваки месец који увек падају на судњи дан.

Као што је споменуто изнад, последњи дан фебруара одређује судњи дан. За јануар, 3. јануар је судњи дан током непреступних година, ток је 4. јануар за преступне године, који се могу запамтити као трећи током три од 4 године, и као четврти у четвртој години. За март, може се запамтити псеудо датум 0. март, који се односи на дан пре 1. марта то јест последњи дан фебруара.

За месеце од априла до децембра, судњи дани су они са истим редним бројем дана и редним бројем месеца уз то да је месец паран (4.4. 6.6. 8.8. 10.10. 12.12.) где сви могу да се рачунају као судњи дан. Непаран број месеци може да се запамти као мнемоник „Ја радим од 9 до 5 у 7-11 радњи“ јер су 9/5, 7/11 судњи дани, као и 5/9 и 11/7 који су такође судњи дани.

Месец	Лак датум	Месец/Дан	Мнемоник
Јануар	3. јануар (непреступне године), 4. јануар (преступна година)	1/3 или 1/4	трећа година у четири и четврти у четвртој
Фебруар	28. фебруар (непреступне године), 29. фебруар (преступна година)	2/28 или 2/29	последњи дан фебруара
Март	"0 Март"	3/0	последњи дан фебруара
Април	4. аpril	4/4	4/4, 6/6, 8/8, 10/10, 12/12
Мај	9. мај	5/9	9-до-5 у 7-11
Јун	6. јун	6/6	4/4, 6/6, 8/8, 10/10, 12/12
Јул	11. јул	7/11	9-до-5 у 7-11
Август	8. август	8/8	4/4, 6/6, 8/8, 10/10, 12/12
Септембар	5. септембар	9/5	9-до-5 у 7-11
Октобар	10. октобар	10/10	4/4, 6/6, 8/8, 10/10, 12/12
Новембар	7. новембар	11/7	9-до-5 у 7-11
Децембар	12. децембар	12/12	4/4, 6/6, 8/8, 10/10, 12/12

Пошто је судњи дан за одређену годину директно повезан са чињеницом да ли се питамо за преступну или непреступну годину, мора се успоставити разлика за јануар и фебруар те године.

Примери

Да би се нашао дан недеље католичког божића 2006. године (2008 судњи дан је био уторак). Пошто је 12. децембар судњи дан, 25. децембар ће пошто је тринаести дан после 12. бити понедељак.

Треба и напоменути да божић увек пада на дан пре судњег дана те године. Уз то 4. јул (амерички празник дана државности) је увек судњи дан, као и ноћ вештица (31. октобар).

Да би се нашао дан недеље за терористички напад на „Близнакиње“ који се десио 11. септембра 2001. године морамо прво да знамо да је датум „сидро“ века уторак, и да је судњи дан за 2001. био један дан унапред, то јест среда. 5. септембар је ту најближи судњи дан, а 11. септембар је 6 дана касније и пада на уторак.

Налажење судњег дана године

Прво узимамо датум „сидро“ века. Следећа табела показује те датуме за векове од 1800 – 1899, 1900 – 1999, 200 – 2099, 2100 – 2199.

Век	Сидро	Мнемоник	Индекс (дан недеље)
1800–1899	Friday	—	5 (Fiveday)
1900–1999	Wednesday	We-in-dis-day (most living people were born in that century)	3 (Treblesday)
2000–2099	Tuesday	Y-Tue-K or Twos-day (Y2K was at the head of this century)	2 (Twosday)
2100–2199	Sunday	Twenty-one-day is Sunday (2100 is the start of the next century)	0 (Noneday)

Даље, тражимо судњи дан године. Да бисмо ово постигли према Конвеју:

Поделимо последње две цифре године (тај број ћемо звати y) са 12, и нека а буде floor тог количника
Нека b буде остатак те једначине
Поделимо тај остатак са 4 и нека c буде floor количника.
Нека d буде сума три броја (d = а + b + c). (Овде је могуће опет поделити сума са 7 и онда узети остатак. Овај број је еквивалентан суми последње две цифре узете године плус floor те две цифре подељен са 4).
Избројмо унапред напоменуте бројеве дана (d или остатак од дељења д са 7) из сидра да би се добио судњи дан те године.

За 20. век година је 1966. на пример:

Као што је описано у тачки 4 изнад, то је еквивалентно са:

Тако да судњи дан за 1966. пада на понедељак.

Слично, судњи дан за нпр. 1966. је такође понедељак:

Зашто ово ради

Рачунање судњег дана је тачно израчунавање броја дана између било ког датума у базној години са и истог датума у тренутној години, а онда остатак модулирати са 7. Када оба датума долазе после преступне године, разлика је само 365у + у/4 (заокружено). Али 365 је једнако 52 * 7 + 1, тако да када склонимо остатак остаје нам

То нам даје једноставну формулу ако је корисник способан да дели велике броје у са 4 и 7. На пример можемо да израчунамо:

Што даје исто решење као у примеру изнад.

Број 12 улази у алгоритам када се узорак (у + у/4)mod 7 скоро понавља сваких 12 година. После 12 година, добијамо (12 + 12/4) mod 7 = 15 mod 7 = 1. Ако заменимо у са у mod12, онда одбацујемо тај додатни дан.

Метода „непар + 11“

Једноставнија метода за налажење судњег дана године је откривена 2010. године и описана је у истраживању Фонга и Волтерса које је објављено. Ова метода је еквивалентна

\left(y+\left\lfloor {\frac {y}{4}}\right\rfloor \right){\bmod {7}}

.

Врло је прилагођена рачунању у глави, зато што јој није потребно дељење са 4 или 12, а процедура се лако памти јер се понавља кључно правило.

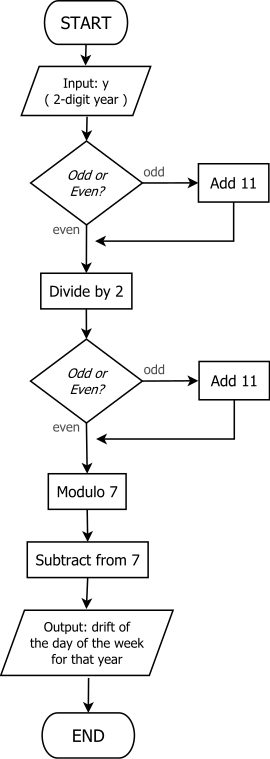
Ако проширимо ово на налажење судњег дана, процедура се често описује као акумулација укупно 6 корака, који следе:

Нека Т буду последње две цифре године
Ако је Т непарно, додај 11
Сад подели Т са два
Ако је т непарно, додај 11
Сада нека Т буде T = 7 − (T mod 7).
Број Т дана унапред од сидра века да би се добио судњи дан године

Ако применимо ову методу на 2005. на пример, кораци изгледају овако:

$T = 5$
$T = 5 + 11 = 16$ (додајемо 11 јер је Т непарно)
$T = 16 / 2 = 8$
$T = 8$ (не радимо ништа јер је Т парно)
$T = 7 - (8 mod 7) = 7 - 1 = 6$
Судњи дан за 2005 = 6 + уторак = понедељак

Експлицитна формула ове методе је:

-\left\lfloor {\frac {y+11(y\,{\bmod {2}})}{2}}+11\left({\frac {y+11(y\,{\bmod {2}})}{2}}{\bmod {2}}\right)\right\rfloor {\bmod {7}}

.

Иако во можда може да изгледа застрашујуће и компликовано, у тсвари је врло једноставно јер је заједнички подизраз $y + 11(y mod 2) / 2$ који мора само једном да се израчуна.

Метода слова

Годинин судњи дан (DD) такође може да се израчуна и са радом са словима године (DL).

DD = (3 - DL) mod 7

Напомена: A = 1, B = 2, ..., G = 0.

За годину 1966. слово је B, тако да је судњи дан DD = 3-2 =1 = понедељак.

Судњи дан	Слово
Недеља	C, DC
Понедељак	B, CB
Уторак	A, BA
Среда	G, AG
Четвртак	F, GF
Петак	E, FE
Субота	D, ED

Проналазак „сидра“ века

За Грегоријански календар:

5 \times (c mod 4) mod 7 +

уторак = сидро.

За Јулијански календар:

6 \times (c mod 7) mod 7 +

недеља = сидро.

Напомена: $c = ⌊.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}year/100⌋$ .

Преглед свих судњих дана

Месец	Датум	Број седмице *
Јануар (непреступне године)	3, 10, 17, 24, 31	1–5
Јануар (преступне године)	4, 11, 18, 25	1–4
Фебруар (common years)	7, 14, 21, 28	6–9
Фебруар (leap years)	1, 8, 15, 22, 29	5–9
Март	7, 14, 21, 28	10–13
Април	4, 11, 18, 25	14–17
Мај	2, 9, 16, 23, 30	18–22
Јун	6, 13, 20, 27	23–26
Јул	4, 11, 18, 25	27–30
Август	1, 8, 15, 22, 29	31–35
Септембар	5, 12, 19, 26	36–39
Октобар	3, 10, 17, 24, 31	40–44
Новембар	7, 14, 21, 28	45–48
Децембар	5, 12, 19, 26	49–52

Тако је у непреступној години дан недеље је један мањи од недеље.

Компјутерска формула за проналажење судњег дана године

За употребу и рад са рачунарима, следеће формула за проналазак судњег дана је врло прикладна:

За Грегоријански календар:

{\mbox{Doomsday}}={\mbox{Tuesday}}+y+\left\lfloor {\frac {y}{4}}\right\rfloor -\left\lfloor {\frac {y}{100}}\right\rfloor +\left\lfloor {\frac {y}{400}}\right\rfloor ={\mbox{Tuesday}}+5\times (y{\bmod {4}})+4\times (y{\bmod {1}}00)+6\times (y{\bmod {4}}00)

На пример, година 2009. има судњи дан недељу према Грегоријанском календару.

{\mbox{Saturday (6)}}{\bmod {7}}={\mbox{Tuesday (2)}}+2009+\left\lfloor {\frac {2009}{4}}\right\rfloor -\left\lfloor {\frac {2009}{100}}\right\rfloor +\left\lfloor {\frac {2009}{400}}\right\rfloor

Као други пример, година 1946 има судњи дан четвртак:

{\mbox{Thursday (4)}}{\bmod {7}}={\mbox{Tuesday (2)}}+1946+\left\lfloor {\frac {1946}{4}}\right\rfloor -\left\lfloor {\frac {1946}{100}}\right\rfloor +\left\lfloor {\frac {1946}{400}}\right\rfloor

За Јулијански каледнар:

{\mbox{Doomsday}}={\mbox{Sunday}}+y+\left\lfloor {\frac {y}{4}}\right\rfloor ={\mbox{Sunday}}+5\times (y{\bmod {4}})+3\times (y{\bmod {7}})

Ова формула може и да се примени на пролептични Грегоријански календар и на пролептични Јулијански календар. Они користе floor функцију и астрономско бројање година за године пре нове ере.

За поређење, погледати рачунање у Јулијанском календару.

Циклус судњих дана од 400 година

Од кад се увео Грегоријански календар, прошло је 146 097 дана, или тачно 20 871 седмица, у 400 година, сидро се понавља свака 4 века. На пример сидро за 1700 – 1799 је сито као и сидро за 2100 – 2199, то јест недеља.

Потпуни 400- годишњи циклус је приказан у табели испод. Векови су за Грегоријански и пролептични Грегоријански календар, сем ако нису обележени са Ј што означава Јулијански. Грегоријанске преступне године су означене.

Јулијански векови ——— Грегоријански векови \ Године	-1600J -900J -200J 500J 1200J 1900J 2600J 3300J — -1600 -1200 -800 -400 0 400 800 1200 1600 2000 2400 2800 3200 3600	-1500J -800J -100J 600J 1300J 2000J 2700J 3400J —	-1400J -700J 0J 700J 1400J 2100J 2800J 3500J — -1500 -1100 -700 -300 100 500 900 1300 1700 2100 2500 2900 3300 3700	-1300J -600J 100J 800J 1500J 2200J 2900J 3600J —	-1200J -500J 200J 900J 1600J 2300J 3000J 3700J — -1400 -1000 -600 -200 200 600 1000 1400 1800 2200 2600 3000 3400 3800	-1100J -400J 300J 1000J 1700J 2400J 3100J 3800J —	-1000J -300J 400J 1100J 1800J 2500J 3200J 3900J — -1300 -900 -500 -100 300 700 1100 1500 1900 2300 2700 3100 3500 3900
00 28 56 84	Уто.	Пон.	Нед.	Суб.	Пет.	Чет.	Сре.
01 29 57 85	Сре.	Уто.	Пон.	Нед.	Суб.	Пет.	Чет.
02 30 58 86	Чет.	Сре.	Уто.	Пон.	Нед.	Суб.	Пет.
03 31 59 87	Пет.	Чет.	Сре.	Уто.	Пон.	Нед.	Суб.
04 32 60 88	Нед.	Суб.	Пет.	Чет.	Сре.	Уто.	Пон.
05 33 61 89	Пон.	Нед.	Суб.	Пет.	Чет.	Сре.	Уто.
06 34 62 90	Уто.	Пон.	Нед.	Суб.	Пет.	Чет.	Сре.
07 35 63 91	Сре.	Уто.	Пон.	Нед.	Суб.	Пет.	Чет.
08 36 64 92	Пет.	Чет.	Сре.	Уто.	Пон.	Нед.	Суб.
09 37 65 93	Суб.	Пет.	Чет.	Сре.	Уто.	Пон.	Нед.
10 38 66 94	Нед.	Суб.	Пет.	Чет.	Сре.	Уто.	Пон.
11 39 67 95	Пон.	Суб.	Суб.	Пет.	Чет.	Сре.	Уто.
12 40 68 96	Сре.	Уто.	Пон.	Нед.	Суб.	Пет.	Чет.
13 41 69 97	Чет.	Сре.	Уто.	Пон.	Нед.	Суб.	Пет.
14 42 70 98	Пет.	Чет.	Сре.	Уто.	Пон.	Нед.	Суб.
15 43 71 99	Суб.	Пет.	Чет.	Сре.	Уто.	Пон.	Нед.
16 44 72	Пон.	Нед.	Суб.	Пет.	Чет.	Сре.	Уто.
17 45 73	Уто.	Пон.	Нед.	Суб.	Пет.	Чет.	Сре.
18 46 74	Сре.	Уто.	Пон.	Нед.	Суб.	Пет.	Чет.
19 47 75	Чет.	Сре.	Уто.	Пон.	Нед.	Суб.	Пет.
20 48 76	Суб.	Пет.	Чет.	Сре.	Уто.	Пон.	Нед.
21 49 77	Нед.	Суб.	Пет.	Чет.	Сре.	Уто.	Пон.
22 50 78	Пон.	Нед.	Суб.	Пет.	Чет.	Сре.	Уто.
23 51 79	Уто.	Пон.	Нед.	Суб.	Пет.	чет.	Сре.
24 52 80	Чет.	Сре.	Уто.	Пон.	Нед.	Суб.	Пет.
25 53 81	Пет.	Чет.	Сре.	Уто.	Пон.	Нед.	Суб.
26 54 82	Суб.	Пет.	Чет.	Сре.	Уто.	Пон.	Нед.
27 55 83	Нед.	Суб.	Пет.	Чет.	Сре.	Уто.	Пон.

Негативне године користе астрономско бројање. Година 25. п. н. е. је -24, као што је приказано у колони.

**Понављање грегоријанских судњих дана у циклусу од 400 година по данима и типу године:**
Недеља	Понедељак	Уторак	Среда	Четвртак	Петак	Субота	Укупно
Непреступне године	43	43	43	43	44	43	44	303
Преступне године	13	15	13	15	13	14	14	97
Укупно	56	58	56	58	57	57	58	400

Преступна година са понедељком као судњим даном значи да је недеља једна од 97 прескочених дана у секвенци од 497-дмо дневне секвенце. Тако је укупан број година са недељом као судњим даном једнак 71 минус број преступних година са понедељком као судњим даном итд. Пошто је понедељак као судњи дан прескочен 29. фебруара 2000. године и патерн преступних дана је симетричан са тим даном, понављање судњих дана по данима недеље (додајемо преступне и непреступне године) су симетричне са понедељком. Понављање судњих дана у преступним годинама су симетрични са судњим даном 2000. године то јест уторком.

Понављање конкретног дана као неког дана седмице може лако се добије из формуле изнад.

На пример, 28. фебруар је један дан после судњег дана претходне године, тако да је 58 пута уторак, четвртак и недеља итд. 29. фебруар је судњи дан преступне године, тако да је 15 пута сваки понедељак и среда.

Циклус од 28 година

Ако гледамо понављање судњих дана у јулијанском 28-одневном циклусу, постоји 1 преступна година и 3 непреступне године за сваки дан седмице, непреступне 6, 17, и 23 године после преступне (са интервалима од 6, 11, 6, и 5 година; неравномерно распоређене јер после 12 година дан је прескочен у секвенци судњих дана). Исти циклус се може применити да било који датум од 1. марта који пада на одређени дан седмице.

За сваки задати датум све то 28. фебруара који пада на одређени дан, 3 заједничке године су 5, 11, и 22 године после преступне године, са интервалима 5, 6, 11 и 6 година. Тако да је циклус исти, али са петогодишњим интервалом после уместо пре преступне године.

Дакле, за сваки датум сем за 29. фебруар, интервали између непруступних година које падају на одређени дан недеље су 6, 11, 11.

За 29. фебруар који пада на одређени дан седмице постоји само један у сваких 28 година, и наравно, преступна је година.

Јулијански календар

Грегоријански календар прецизно се равна са астрономским дешавањима као што су равнодневнице, краткодневнице и дугодневнице. Током 1582. се увела ова модификација у Јулијаноски календар. Да би се исправила грешка у календару, 10 дана су прескочени, тако да је судљи дан померен 10 дана уназад. Табела укључује године Јулијанског календара, али је алгоритам за Грегоријански и пролептични Грегоријански календар.

Треба напоменути да Грегоријански календар није прихваћен у свим земљама у истом тренутку, тако да за многе земље, различите регије су користиле различите датуме за исти дан.

Потпуни примери

Пример 1 (1985)

Претпоставимо да знамо дан недеље за 8. септембар 1985. године. Почињемо са сидром века, средом. Овоме ћемо додати три ствари, и зовемо их a, b, c:

a је floor од 85/12, што је 7
b је 85 мод 12, што је 1
c је floor b/4 што је 0

Из овога добијамо да је a+b+c = 8. Бројимо 8 дана од среде, долазимо да четвртка, што јесте судњи дан за 1985. годину. Сада поредимо 18. септембар са блиским судњим даном, 5. септембром. Видимо да је 18. 13 дана од судњег то јест један дан мање од две недеље.

Пример 2 (остали векови)

Претпоставимо да желимо да нађемо дан седмице на који је избио Амерички цивилни рат, који се десио 12. априла 1861. Сидро за прошли век је било 99 дана од четвртка, или, другим речима петак (израчунат као (18 + 1) × 5 + ⌊18/4⌋; или можемо само да погледамо у табелу изнад, која приказује сидра за векове). Цифре 61 имају размак од 6 дана до судњег дана, четвртка. Дакле, 4. април је био четвртак, тако да је 12. априли, 8 дана касније био петак.

Референце

^ John Horton Conway, "Tomorrow is the Day After Doomsday", Eureka, volume 36, pages 28–31, October 1973.
^ Richard Guy, John Horton Conway, Elwyn Berlekamp : "Winning Ways: For Your Mathematical Plays, Volume. 2: Games in Particular", pages 795–797, Academic Press, London. 1982. ISBN 978-0-12-091102-8.
^ Carroll, Lewis (1887). „To Find the Day of the Week for any Given Date”. Nature. 35 (909): 517. Bibcode:1887Natur..35..517C. S2CID 4077610. doi:10.1038/035517a0.
^ Martin Gardner, "The Universe in a Handkerchief: Lewis Carroll's Mathematical Recreations, Games, Puzzles, and Word Plays", pages 24–26, Springer-Verlag, 1996
^ Alpert, Mark (1999). „Not Just Fun and Games”. Scientific American. 280 (4): 40—42. Bibcode:1999SciAm.280d..40A. doi:10.1038/scientificamerican0499-40.

Спољашње везе

Encyclopedia of Weekday Calculation by Hans-Christian Solka, 2010
Doomsday calculator that also "shows all work"
World records for mentally calculating the day of the week in the Gregorian Calendar
What is the day of the week, given any date?
Doomsday Algorithm
Finding the Day of the Week
„Poem explaining the Doomsday rule”. Архивирано из оригинала 18. 10. 2006. г. Приступљено 09. 01. 2016.

[1] John Horton Conway, "Tomorrow is the Day After Doomsday", Eureka, volume 36, pages 28–31, October 1973.

[2] Richard Guy, John Horton Conway, Elwyn Berlekamp : "Winning Ways: For Your Mathematical Plays, Volume. 2: Games in Particular", pages 795–797, Academic Press, London. 1982. ISBN 978-0-12-091102-8.

[3] Carroll, Lewis (1887). „To Find the Day of the Week for any Given Date”. Nature. 35 (909): 517. Bibcode:1887Natur..35..517C. S2CID 4077610. doi:10.1038/035517a0.

[4] Martin Gardner, "The Universe in a Handkerchief: Lewis Carroll's Mathematical Recreations, Games, Puzzles, and Word Plays", pages 24–26, Springer-Verlag, 1996

[5] Alpert, Mark (1999). „Not Just Fun and Games”. Scientific American. 280 (4): 40—42. Bibcode:1999SciAm.280d..40A. doi:10.1038/scientificamerican0499-40.

[1]

[2]

[3]

[4]

[5]