С Википедије, слободне енциклопедије
Параболички координатни систем у две димензије има координатне линије представљене конфокалним параболама . У три димензије параболичке координате се добијају ротирањем дводимензионалнога система око оси симетрије парабола .
У дводимензионалном систему параболичке координате
(
σ
,
τ
)
{\displaystyle (\sigma ,\;\tau )}
x
=
σ
τ
,
{\displaystyle x=\sigma \tau ,}
y
=
1
2
(
τ
2
−
σ
2
)
.
{\displaystyle y={\frac {1}{2}}(\tau ^{2}-\sigma ^{2}).}
Криве константнога
σ
{\displaystyle \sigma }
2
y
=
x
2
σ
2
−
σ
2
{\displaystyle 2y={\frac {x^{2}}{\sigma ^{2}}}-\sigma ^{2}}
које су отворене нагоре. С друге стране криве константнога
τ
{\displaystyle \tau }
2
y
=
−
x
2
τ
2
+
τ
2
{\displaystyle 2y=-{\frac {x^{2}}{\tau ^{2}}}+\tau ^{2}}
које су отворене надоле. Фолуси обе параболе су у исходишту.
Ламеови коефицијенти параболичких координата су:
H
σ
=
H
τ
=
σ
2
+
τ
2
.
{\displaystyle H_{\sigma }=H_{\tau }={\sqrt {\sigma ^{2}+\tau ^{2}}}.}
Елементи површине су:
d
S
=
(
σ
2
+
τ
2
)
d
σ
d
τ
,
{\displaystyle dS=(\sigma ^{2}+\tau ^{2})\,d\sigma \,d\tau ,}
а Лапласијан је:
Δ
Φ
=
1
σ
2
+
τ
2
(
∂
2
Φ
∂
σ
2
+
∂
2
Φ
∂
τ
2
)
.
{\displaystyle \Delta \Phi ={\frac {1}{\sigma ^{2}+\tau ^{2}}}\left({\frac {\partial ^{2}\Phi }{\partial \sigma ^{2}}}+{\frac {\partial ^{2}\Phi }{\partial \tau ^{2}}}\right).}
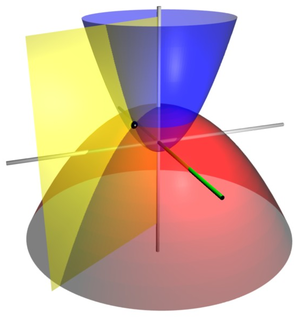
Постоје два облика тродимензионалних параболичких координата. Према једној верзији параболе се ротирају око своје оси симетрије, па је трансформација координата:
x
=
σ
τ
cos
φ
{\displaystyle x=\sigma \tau \cos \varphi }
y
=
σ
τ
sin
φ
{\displaystyle y=\sigma \tau \sin \varphi }
z
=
1
2
(
τ
2
−
σ
2
)
{\displaystyle z={\frac {1}{2}}\left(\tau ^{2}-\sigma ^{2}\right)}
Ос параболопоида слаже се са
z
{\displaystyle z}
ϕ
{\displaystyle \phi }
tan
φ
=
y
x
{\displaystyle \tan \varphi ={\frac {y}{x}}}
Површи константнога
σ
{\displaystyle \sigma }
2
z
=
x
2
+
y
2
σ
2
−
σ
2
{\displaystyle 2z={\frac {x^{2}+y^{2}}{\sigma ^{2}}}-\sigma ^{2}}
који су отворени нагоре. Површи константнога
τ
{\displaystyle \tau }
2
z
=
−
x
2
+
y
2
τ
2
+
τ
2
{\displaystyle 2z=-{\frac {x^{2}+y^{2}}{\tau ^{2}}}+\tau ^{2}}
који су отворени надоле.
Риманов метрички тензор тога координатнога система је:
g
i
j
=
[
σ
2
+
τ
2
0
0
0
σ
2
+
τ
2
0
0
0
σ
2
τ
2
]
{\displaystyle g_{ij}={\begin{bmatrix}\sigma ^{2}+\tau ^{2}&0&0\\0&\sigma ^{2}+\tau ^{2}&0\\0&0&\sigma ^{2}\tau ^{2}\end{bmatrix}}}
Ламеови коефицијенти параболичких координата у тродимензионалном простору су:
H
σ
=
σ
2
+
τ
2
,
{\displaystyle H_{\sigma }={\sqrt {\sigma ^{2}+\tau ^{2}}},}
H
τ
=
σ
2
+
τ
2
,
{\displaystyle H_{\tau }={\sqrt {\sigma ^{2}+\tau ^{2}}},}
H
φ
=
σ
τ
.
{\displaystyle H_{\varphi }=\sigma \tau .}
Инфинитезимална запремина је онда дана са:
d
V
=
h
σ
h
τ
h
φ
=
σ
τ
(
σ
2
+
τ
2
)
d
σ
d
τ
d
φ
,
{\displaystyle dV=h_{\sigma }h_{\tau }h_{\varphi }=\sigma \tau (\sigma ^{2}+\tau ^{2})\,d\sigma \,d\tau \,d\varphi ,}
а Лапласијан је
∇
2
Φ
=
1
σ
2
+
τ
2
[
1
σ
∂
∂
σ
(
σ
∂
Φ
∂
σ
)
+
1
τ
∂
∂
τ
(
τ
∂
Φ
∂
τ
)
]
+
1
σ
2
τ
2
∂
2
Φ
∂
φ
2
.
{\displaystyle \nabla ^{2}\Phi ={\frac {1}{\sigma ^{2}+\tau ^{2}}}\left[{\frac {1}{\sigma }}{\frac {\partial }{\partial \sigma }}\left(\sigma {\frac {\partial \Phi }{\partial \sigma }}\right)+{\frac {1}{\tau }}{\frac {\partial }{\partial \tau }}\left(\tau {\frac {\partial \Phi }{\partial \tau }}\right)\right]+{\frac {1}{\sigma ^{2}\tau ^{2}}}{\frac {\partial ^{2}\Phi }{\partial \varphi ^{2}}}.}
{
x
=
ξ
η
cos
φ
,
y
=
ξ
η
sin
φ
,
z
=
1
2
(
ξ
−
η
)
.
{\displaystyle {\begin{cases}x={\sqrt {\xi \eta }}\cos \varphi ,\\y={\sqrt {\xi \eta }}\sin \varphi ,\\z={\dfrac {1}{2}}(\xi -\eta ).\end{cases}}}
Ламеови коефицијенти су онда:
H
ξ
=
ξ
+
η
2
ξ
H
η
=
ξ
+
η
2
η
H
φ
=
η
ξ
{\displaystyle {\begin{matrix}H_{\xi }={\frac {\sqrt {\xi +\eta }}{2{\sqrt {\xi }}}}\\H_{\eta }={\frac {\sqrt {\xi +\eta }}{2{\sqrt {\eta }}}}\\H_{\varphi }={\sqrt {\eta \xi }}\end{matrix}}}
Инфинитезимална запремина је онда дана са:
d
V
=
ξ
+
η
4
d
ξ
d
η
d
φ
,
{\displaystyle dV={\frac {\xi +\eta }{4}}\,d\xi \,d\eta \,d\varphi ,}
а Лапласијан је
∇
2
Φ
=
4
ξ
+
η
[
∂
∂
ξ
(
ξ
∂
Φ
∂
ξ
)
+
∂
∂
η
(
η
∂
Φ
∂
η
)
]
+
1
ξ
η
∂
2
Φ
∂
φ
2
.
{\displaystyle \nabla ^{2}\Phi ={\frac {4}{\xi +\eta }}\left[{\frac {\partial }{\partial \xi }}\left(\xi {\frac {\partial \Phi }{\partial \xi }}\right)+{\frac {\partial }{\partial \eta }}\left(\eta {\frac {\partial \Phi }{\partial \eta }}\right)\right]+{\frac {1}{\xi \eta }}{\frac {\partial ^{2}\Phi }{\partial \varphi ^{2}}}.}
Параболичке координате Korn GA and Korn TM. (1961) Mathematical Handbook for Scientists and Engineers , McGraw-Hill.
Abramowitz, Milton; Stegun, Irene A., eds. (1965), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover. ISBN 978-0-486-61272-0 .
Morse PM, Feshbach H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill. 1953. ISBN 978-0-07-043316-8 . 
























![{\displaystyle \nabla ^{2}\Phi ={\frac {1}{\sigma ^{2}+\tau ^{2}}}\left[{\frac {1}{\sigma }}{\frac {\partial }{\partial \sigma }}\left(\sigma {\frac {\partial \Phi }{\partial \sigma }}\right)+{\frac {1}{\tau }}{\frac {\partial }{\partial \tau }}\left(\tau {\frac {\partial \Phi }{\partial \tau }}\right)\right]+{\frac {1}{\sigma ^{2}\tau ^{2}}}{\frac {\partial ^{2}\Phi }{\partial \varphi ^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c364ac2414a85d4b98704013938e5776593acb8b)



![{\displaystyle \nabla ^{2}\Phi ={\frac {4}{\xi +\eta }}\left[{\frac {\partial }{\partial \xi }}\left(\xi {\frac {\partial \Phi }{\partial \xi }}\right)+{\frac {\partial }{\partial \eta }}\left(\eta {\frac {\partial \Phi }{\partial \eta }}\right)\right]+{\frac {1}{\xi \eta }}{\frac {\partial ^{2}\Phi }{\partial \varphi ^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eea9b78c5471fd03f37e5148f94cc457bc165cbb)