Подударност (геометрија)

Пример подударности. Два троугла лево су подударна, док је трећи сличан њима. Задњи троугао није ни сличан ни подударан са осталима. Подударност дозвољава измене неких својстава, као што су локација и оријентација, али оставља остале непромењеним, као што су растојање и углови. Непромењена својства се називају инваријантама.

Овај дијаграм илуструје геометријски принцип „угао-угао-страна” подударности: Ако су дати троуглови ABC и A'B'C', троугао ABC је подударан са троуглом A'B'C' ако и само ако је угао CAB подударан са C'A'B' и угао ABC је подударан са A'B'C', и БЦ је подударно са B'C'

У геометрији две фигуре су подударне ако имају исту величину и облик, или ако једна има исти облик и величину као слика у огледалу друге. Два скупа тачака су подударна ако постоји пресликавање којим се тај скуп пресликава у други скуп, а да се при том не мења величина и облик.

Подударност се означава са $\cong$

Подударан има значење:

1. Две дужи су подударне ако имају исту дужину $d_{1}=d_{2}$ тј $d_{1}\cong d_{2}$
2. Два угла су подударна ако имају исту меру $\alpha _{1}=\alpha _{2}$ тј $\alpha _{1}\cong \alpha _{2}$
3. Два круга су подударна ако имају исти пречник $R_{1}\cong R_{2}$ тј $R_{1}\cong R_{2}$

Одређивање подударности полигона

Наранџасти и зелени четвороугао су подударни; плави није конгруентан са њима. Сва три имају исти обим и површину. (Редослед страница плавог четвороугла је „помешан“ што доводи до тога да два унутрашња угла и једна од дијагонала нису подударни.)

Да би два полигона била подударна, морају имати једнак број страница (а самим тим и једнак број – исти број – темена). Два полигона са н страна су подударна ако и само ако сваки од њих има нумерички идентичне низове (чак и ако у смеру казаљке на сату за један полигон и супротно од казаљке на сату за други) страница-угао-страница-угао- ... за н страница и н углова.

Конгруенција полигона може се графички утврдити на следећи начин:

• Прво, упарите и означите одговарајуће врхове две фигуре.
• Друго, нацртајте вектор од једног од врхова једне од фигура до одговарајућег темена друге фигуре. Транслирајте прву фигуру овим вектором тако да се ова два темена поклапају.
• Треће, ротирајте транслирану фигуру око подударног темена док се један пар одговарајућих страна не поклопи.
• Четврто, одразите ротирану фигуру око ове упарене стране док се бројке не поклопе.

Ако у било ком тренутку корак не може да се заврши, полигони нису подударни.

Аксиоми подударности

Аксиоми подударности описују основне карактеристике релације подударности парова тачака. Ову релација се уводи као полазни појам.

• Аксиом 1

Ако је $(A,B)\cong (C,D)$ и $A=B$, тада је и $C=D$.

• Аксиом 2

За сваке две тачке $A$ и $B$ је $(A,B)\cong (B,A)$.

• Аксиом 3

Ако је $(A,B)\cong (C,D)$ и $(A,B)\cong (E,F)$ тада је $(C,D)\cong (E,F)$

• Аксиом 4

Ако су C и C' тачке отворених дужи AB и A'B', такве да је $(A,C)\cong (A',C')$ и $(B,C)\cong (B',C')$, тада је и $(B,C)\cong (A',B')$

• Аксиом 5

Ако су A и B две тачке и CX полуправа тада на тој полуправој постоји тачка D таква да је $(A,B)\cong (C,D)$

• Аксиом 6

Ако су A, B, C три неколинеарне тачке и $A',B'$ тачке руба неке полуравни $\pi$, такве да је $(A,B)\cong (A',B')$ тада у тој полуравни постоји јединствена тачка C' таква да је $(A,C)\cong (A',C')$ и $(B,C)\cong (B',C')$

• Аксиом 7

Ако су A, B, C и A', B', C' две тројке неколинеарних тачака и D и D' тачке полуправих BC и B'C' такве да је $(AB)\cong (A',B')$ , $(BC)\cong (B',C')$, $(A,C)\cong (A',C')$ и $(B,D)\cong (B',D')$, тада је и $(A,D)\cong (A',D')$

Релација подударности парова тачака је релација еквиваленције.

1. $(A,B)\cong (A,B)$ релација је рефлексивна.
2. Нека је $(AB)\cong (C,D)$ [$(A,B)\cong (A,B)$] => $(CD)\cong (A,B)$ релација је симетрична
3. $(A,B)\cong (C,D)$ и $(C,D)\cong (E,F)=>$ $(A,B)\cong (E,F)$ [следи на основу симетричности]

Теорема 1

Ако су A и B две тачке и CX полуправа тада на тој полуправој постоји јединствена тачка D таква да је '$(A,B)\cong (CD)$

Теорема 2

Ако су A,B,C три разне тачке праве p и A',B' две тачке праве p' такве да је $(A,B)\cong (A',B')$, тада постоји јединствена тачка C' таква да је A',B' и $(A,C)\cong (A',C')$.

При томе, тачка C' припада правој p' и:

1. ако је ${\mathfrak {B}}(A,C,B)$, тада је ${\mathfrak {B}}(A',C',B')$
2. ако је ${\mathfrak {B}}(A,B,C)$, тада је ${\mathfrak {B}}(A',B',C')$
3. ако је ${\mathfrak {B}}(B,C,A)$, тада је ${\mathfrak {B}}(B',C',A')$

Дефиниција 1

Каже се да је уређена n-торка тачака $(A_{1},A_{2},...,A_{n})$ подударна са n-торком $(A'_{1},A'_{2},...,A'_{n})$ у ознаци $(A_{1},A_{2},...,A_{n})\cong (A'_{1},A'_{2},...,A'_{n})$

ако је за свако $(i,k)\in {\begin{Bmatrix}{1,2,...n}\end{Bmatrix}}(A_{i},A_{k})\cong (A'_{i},A'_{k})$

Дефиниција 2

Нека су А и B две разне тачке неке равни $\alpha$. Скуп свих тачака $X$ те равни таквих да је $(A,B)\cong (A,X)$, назива се круг, у ознаци $k(A,AB)$, са центром А и чији је полупречник дуж AB.

Подударност дужи

Ако су две дужи AB и CD су подударне, то може се означити са $AB\cong CD$

Теорема 3

$(A,B)\cong (A',B')=>A,B\cong A',B'$,

Дефиниција 3

Тачка S је средиште дужи $AB$, ако припада тој дужи и важи $AS\cong SB$

Теорема 4

За сваку дуж постоји јединствено средиште.

Дефиниција 4

Дуж AB је мања од дужи CD у ознаци AB < CD ако унутар дужи CD постоји тачка E таква да је AB ≅ CE. Такође у том случају се каже и да је дуж CD већа од дужи AB у ознаци CD > AB.

Дефиниција 5

Дуж EF једнака је збиру дужи AB и CD у ознаци EF = AB + CD, ако унутар дужи EF постоји тачка G таква да је AB≅EG CD ≅GF.

На исти начин дефинишу се разлика, производ дужи и природног броја, производ дужи ирационалног броја

Подударност углова, прави углови, релација нормалности правих

Два конвексна или конкавна угла $pOq$ и $p_{1}O_{1}q_{1}$ су подударна ако и само ако на крацима $p$ и $q$ $p_{1}$, $q_{1}$ редом постоје тачке $P,Q,P_{1},Q_{1}$ такве да је: $(P,O,Q)\cong (P_{1},O_{1},Q_{1}$).

Теорема 5

• Унакрсни углови су међусобно подударни.
• За сваки ∠pq и сваку полуправу p' неке равни, постоји у полуравни одређеној правом која садржи p', јединствена полуправа q' таква да ∠pq ≅ ∠p'q'.

Теорема 6

Сваки угао има јединствену бисектрису

Дефиниција 5

Угао AOB је мањи од угла CSD у ознаци $\angle AOB<\angle CSD$ ако унутар угла CSD постоји полуправа SE таква да је $\angle AOB\cong \angle CSE$. У том случају кажемо иа је угао CSD већи од угла AOB у ознаци $\angle CSD>\angle AOB$.

Дефиниција 6

Углом две мимоилазне праве p и q у простору $E^{3}$ назива се угао који одређују њима паралелене праве a и b које се секу у некој тачки О. Специјално, ако је угао две мимоилазне праве у простору $E^{3}$ прав, тада се каже да су праве $p$ и $q$ нормалне међу собом, и симболички означавамо са $p\perp q$

Теорема 7

1. Угао подударан неком правом углу такође је прав.
2. Прави углови су међу собом подударни.
3. Постоји једна и само једна права која сече сваку од две мимоилазне праве a и b под правим углом.

Подударност полигона

Иако сва три полигона имају исти обим и површину подударни су само наранџасти и зелани

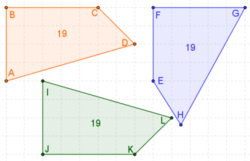
Два подударна полигона имају исти број страница и врхова.

Два полигони са n страна су подударна, ако и само ако сваки од њих има одговарајуће странице и углове једнаке.

Подударност неких правилних четвороуглова

1. Два паралелограма су подударна ако су им подударне две суседне ивице и један угао.
2. Два правоугаоника су подударна ако су им подударне две суседне ивице.
3. Два ромба су подударна ако су им подударне једна ивица и један угао
4. Два квадрата су подударна ако су им подударне странице.

Подударност троуглова

Подударност троуглова

Два троугла су подударна ако су њихове одговарајуће странице једнаке дужине, одговарајући углови једнаке величине. Да су два троугла ABC и DEF подударни записује се

$\triangle \mathrm {ABC} \cong \triangle \mathrm {DEF}$

Одређивање подударностости

• СУС

Два троугла су подударна ако су две ивице и њима захваћени угао једног троугла подударни са одговарајућим ивицама и угловима другог троугла, тј: $AB\cong A'B',AC\cong A'C',\angle BAC\cong \angle B'A'C'=>\triangle ABC\cong \triangle A'B'C'$

• ССС

Два троугла су подударна ако су им одговарајуће ивице подударне, тј. $AB\cong A'B',BC\cong B'C',AC\cong A'C'=>\triangle ABC\cong \triangle A'B'C'$

Доказ:

Нека су ABC, A'B'C' два троугла таква да је $AB\cong A'B',BC\cong B'C',AC\cong A'C'$. Тада су и одговарајући парови тачака подударни тј. $\triangle ABC\cong \triangle A'B'C'.$

Постоји изометрија те равни, која тачке A,B,C пресликава редом у тачке A', B', C'. Изометрије чувају распоред, па се одговарајуће ивице једног троугла пресликавају у одговарајуће ивице другог троугла. Изометрија пресликава троугао ABC у троугао A'B'C', па је $\triangle ABC\cong \triangle A'B'C'.$

• УСУ

Два троугла су подударна ако су једна ивица и на њој налегли углови једног троугла подударни са одговарајућом ивицом и одговарајућим угловима другог троугла, тј: $BC\cong B'C',\angle ABC\cong \angle A'B'C',\angle ACB\cong \angle A'C'B'=>\triangle ABC\cong \triangle A'B'C'$

• ССУ

Два троугла су подударна ако су две ивице и угао наспрам једне од њих једног троугла подударни са одговарајућим страницама и одговарајућим углом другог троугла.

Литература

• Цоxетер, Х. С. M. (1969). Интродуцтион то Геометрy, Сецонд едитион. Wилеy. ИСБН 9780471504580. 
• Боyер, C.Б. (1991) [1989]. А Хисторy оф Матхематицс (Сецонд едитион, ревисед бy Ута C. Мерзбацх изд.). Неw Yорк: Wилеy. ИСБН 978-0-471-54397-8. 
• Цооке, Рогер (2005), Тхе Хисторy оф Матхематицс:, Неw Yорк: Wилеy-Интерсциенце, 632 пагес, ИСБН 978-0-471-44459-6 
• Хаyасхи, Такао (2003), „Индиан Матхематицс”, Ур.: Граттан-Гуиннесс, Ивор, Цомпанион Енцyцлопедиа оф тхе Хисторy анд Пхилосопхy оф тхе Матхематицал Сциенцес, 1, Балтиморе, MD: Тхе Јохнс Хопкинс Университy Пресс, 976 пагес, стр. 118—130, ИСБН 978-0-8018-7396-6 
• Хаyасхи, Такао (2005), „Индиан Матхематицс”, Ур.: Флоод, Гавин, Тхе Блацкwелл Цомпанион то Хиндуисм, Оxфорд: Басил Блацкwелл, 616 пагес, стр. 360—375, ИСБН 978-1-4051-3251-0 
• Николаи I. Лобацхевскy, Пангеометрy, транслатор анд едитор: А. Пападопоулос, Херитаге оф Еуропеан Матхематицс Сериес, Вол. 4, Еуропеан Матхематицал Социетy, 2010.
• Јаy Каппрафф, А Партиципаторy Аппроацх то Модерн Геометрy, Wорлд Сциентифиц Публисхинг. 2014. ISBN 978-981-4556-70-5..
• Леонард Млодиноw, Еуцлид'с Wиндоw – Тхе Сторy оф Геометрy фром Параллел Линес то Хyперспаце, УК едн. Аллен Лане, 1992.
• Хендерсон, Давид W.; Таимина, Даина (2005), Еxпериенцинг Геометрy/Еуцлидеан анд Нон-Еуцлидеан wитх Хисторy (3рд изд.), Пеарсон Прентице-Халл, ИСБН 978-0-13-143748-7 
• Јацобс, Харолд Р. (1974), Геометрy, W.Х. Фрееман анд Цо., ИСБН 978-0-7167-0456-0 
• Педое, Дан (1988) [1970], Геометрy/А Цомпрехенсиве Цоурсе, Довер, ИСБН 978-0-486-65812-4 
• Сиблеy, Тхомас Q. (1998), Тхе Геометриц Виеwпоинт/А Сурвеy оф Геометриес, Аддисон-Wеслеy, ИСБН 978-0-201-87450-1 
• Смарт, Јамес Р. (1998), Модерн Геометриес (5тх изд.), Броокс/Цоле, ИСБН 978-0-534-35188-5 
• Стахл, Саул (2003), Геометрy/Фром Еуцлид то Кнотс, Прентице-Халл, ИСБН 978-0-13-032927-1 
• Венема, Герард А. (2006), Фоундатионс оф Геометрy, Пеарсон Прентице-Халл, ИСБН 978-0-13-143700-5 
• Yале, Паул Б. (1968), Геометрy анд Сyмметрy, Холден-Даy 
• Јудитх Н. Цедерберг (1989, 2001) А Цоурсе ин Модерн Геометриес, Цхаптер 3.12 Симиларитy Трансформатионс, пп. 183–9, Спрингер. ISBN 978-0-387-98972-3. .
• Гüнтер Еwалд (1971) Геометрy: Ан Интродуцтион, пп. 106, 181, Wадсwортх Публисхинг.
• Георге Е. Мартин (1982) Трансформатион Геометрy: Ан Интродуцтион то Сyмметрy, Цхаптер 13 Симиларитиес ин тхе Плане, пп. 136–46, Спрингер. ISBN 978-0-387-90636-2. .

Спољашње везе

• Геометрија
• The SSS at Cut-the-Knot
• The SSA at Cut-the-Knot
• Interactive animations demonstrating Congruent polygons, Congruent angles, Congruent line segments, Congruent triangles at Math Open Reference