Алгоритам очекивања-максимизације
Овај чланак можда захтева чишћење и/или прерађивање како би се задовољили стандарди квалитета Википедије. Проблем: Унос унутрашњих веза и референци. (децембар 2016) |
У статистици, алгоритам максимизације очекиване веродостојности (EM - енгл. Expectation-maximization) је итеративна процедура за процену параметара на основу критеријума максималне веродостојности (МЛ - енгл. Maximum Likelihood) или оцене апостериорног максимума (МАП - енгл. Maximum a posteriori), код којих су присутне вредности посматраних величина које имају особину θ која се не може измерити, или се не може директно измерити (латентне променљиве).
ЕМ алгоритам наизменично примењује "корак Е" у којем се генерише функција очекиване вредности логаритма веродостојности израчунату коришћењем тренутне процене параметара, и "корак М", у којем се израчунавају параметри за које функције генерисана у кораку Е узима максималну вредност. Параметри добијени у кораку М се потом користе за одређивање расподеле латентних варијабли за следећи корак Е.
Историјат[уреди | уреди извор]
Име ЕМ алгоритма и начин функционисања, дато је у раду из 1977. године, који су написали Артур Демпстер, Нан Лаирд и Доналд Рубин.[1] Њихов рад је генерализовао методу и скицирао анализу конвергенције за ширу класу проблема. Без обзира на раније проналаске, њихова иновативна метода се прославила у јавности и њивов рад окатегорисан као брилијантан. Рад Демпстер-Лаирд-Рубин је основао ЕМ метод као веома важан део статистичке анализе.[2][3][4]
Увод[уреди | уреди извор]
ЕМ алгоритам се користи за проналажење параметра максималне веродостојности статистичког модела у случајевима код којих се једначине не могу решити директно. Обично ови модели поред непознатих параметара и познатих резултата мерења укључују и латентне променљиве. То значи да, или недостају неке од мерених вредности, или се модел може формулисати једноставније претпостављајући постојање додатних неизмерених вредности посматраних величина.
Проналажење решења максималне веродостојности захтева узимање извода функције вероватноће по свим непознатим вредностима. Код статистичих модела са латентним променљивима ово обично није могуће. Уместо тога, резултат је скуп међусобно повезаних једначина у којој решење за параметре захтева познавање вредности латентних променљивих и обратно, али замена једног скупа једначина у други доводи до нерешивих једначина. ЕМ алгоритам полази од запажања да се ова два сета једначина могу решити нумерички. То се може извести тако што се изаберу произвољне вредности за један од два скупа непознатих, затим се те произвољне вредности употребе за процену другог скупа, а затим помоћу ових нових вредности нађе боља процена првог скупа. Процедура се наставља итеративно док резултујуће вредности не конвергирају ка фиксним тачкама. Није очигледно да се овим алгоритмом може доћи до решења у општем случају, али се може доказати да је могуће у конкретним случајевима. При томе се извод веродостојности може привести произвољно близу нули, што значи да је пронађена тачка или локални максимум или седласта тачка. Није гарантовано да ће пронађени максимум бити глобални максимум. У неким случајевима функција веродостојности има сингуларитете који обично представљају максимуме без смислене интерпретације у контексту у којем се алгоритам примењује.
Опис алгоритма[уреди | уреди извор]
Дати статистички модел који се састоји од скупа посматраних података, скуп непримећених латентних података или вредности које недостају и вектр непознатих параметара , заједно са функцијом веродостојности , процена максималне веродостојности (МЛЕ - енгл. Maximum likelihood estimate) од непознатих параметара одређује маргиналне веродостојности посматраних података
Међутим, ово је често нерешиво (нпр. Ако се деси да број вредности расте експоненцијално што је секвенца дужа, онда ће тачан прорачун суме бити изузетно тежак).
ЕМ алгоритам покушава да пронађе МЛЕ од граничне веродостојности итеративном применом следећа два корака:
- Корак очекивања (Е корак): Израчунава очекивану вредност лог веродостојности функције вероватноће, у погледу на условну расподелу датим под тренутном проценом параметара :
- Корак максимизације (М корак): Проналази параметар који максимизује следеће:
Типични модели на које се примењује ЕМ:
- Посматране тачке података могу бити дискретне (узимајући вредности из коначног или пребројиво бесконачног скупа) или непрекидне (узмањући вредности из непребројиво бесконачног скупа). Могу, у ставри, бити и вектор опсевације повезан са сваком тачком података.
- Вредности које недостају (латентне варијабле) су дискретне, извучене из фиксног броја вредности, а постоји једна латентна променљива по посматраној тачки података.
- Параметри су непрекидни, и има две врсте: Параметри који су повезани са свим тачкама података, и параметара повезаним са одређеном вредношћу латентне варијабле.
Међутим, могуће је да се ЕМ примени и на друге врсте модела. Ако знамо вредности параметара , обично се може наћи вредност латентних варијабли повећавањем лог-веродостојности по свим могућим вредностима , или једноставно итеративно преко или преко алгоритма, као што је Витерби алгоритам за скривене Маркове моделе. Насупрот томе, ако знамо вредности латентних варијабли , можемо наћи процену параметрара прилично лако, једноставним груписањем посматране тачке података на основу вредности придружене латенте варијабле и просека вредности, или нека функција вредности, од тачака у свакој групи. Ово сугерише итеративни алгоритам, у случају када су и непознати:
- Прво, иницијализујте параметре неким случајним вредностима.
- Израчунај најбољу вредност за помоћу ових вредности параметара.
- Затим, користите ове израчунате вредности да израчунате бољу процену параметара . Параметри повезани са одређеном вредношћу ће користити само оне тачке података код којих придружене латентне варијабле имају ту вредност.
- Вршите итерацију корака 2 и 3 до конвергенције.
Управо описан алгоритам монотоно прилази локаном минимуму функције, а најчешће се назива хард ЕМ. K-mean алгоритам је пример ове класе алгоритма.
Својства[уреди | уреди извор]
Говорећи о Е кораку, мало је погрешан. Оно што се рачуна у првом кораку су фиксни параметри зависни од података функције Q. Када су параметри Q познати, потпуно су одређени и увећани у другом М кораку ЕМ алогритма.
Иако ЕМ итерација повећава број посматраних података (тј. маргинали) функције веродостојности, не постоји гаранција да низ конвергира ка процени максималне веродостојности (МЛЕ). За бимодалне дистрибуције, ово значи да ЕМ алгоритам може конвергирати до локалног максимума посматраних података функције веродостојности, зависећи од почетних вредности. Постоји низ хеуристичких или метахеуристичких приступа за "бежање" локалним максимумима, као што су насумични рестарт (кренувши од неколико различитих случајних почетних процена θ(t)), или применом алгоритма симулације жарења.
ЕМ је нарочито користан када је веродостојност у породици експоненцијалних алгоритама: Е корак постаје збир очекивања довољне статистике, а М корак подразумева максимизовање линеарне функције. У том случају обично је могуће извести исправке у затвореној форми за сваки корак, користећи Сундберг формулу (Објавио Ралф Сундберг користећи необјављене резултате Пер Мартин–Лофа и Андерс Мартин-Лофа).
ЕМ метода је модификована за израчунавање максималне апостериорне процене (МАП), са Бајесовом статистиком, у оригиналном раду Демпстер, Лаирд и Рубин.
Постоје и друге методе за проналажење максималне веродостојности, једна од метода је варијација Гаус-Њутновог алгоритма, а постоје и још неке. За разлику од ЕМ, такве методе обично захтевају процену првог или другог деривата функције веродостојности.
Доказ коректности[уреди | уреди извор]
ЕМ алгоритам ради на побољшању , а не побољшава директно . Овде смо показали да побољшања првог подразумева побољшање последњг. За било које са не нултом вероватноћом , можемо записати
Узимамо очекивање над вредностима множењем обе стране са . Сабирањем и (или интегрисањем) преко . Лева страна је константа очекивања, па добијамо:
где је одређен негирањем суме коју је заменио. Ова последња једначина важи за било коју вредност , uključujući ,
и одузимањем ове последње једначине са оном из претходне, добијамо
Међутим, Гисова неједнакост нам говори да , па можемо закључити да
Другим речима, бирајући да унапредимо изван ће унапредити preko најмање толико.
Апликације[уреди | уреди извор]
Под неким околностима, врло је згодно гледати на ЕМ алгоритам као два наизменична корака максимизирања. Размотримо функцију:
где је q произвољна расподела вероватноћа над непосматраним подацима z, pZ|X(· |x;θ) је условна расподела непосматраних података где су дати посматрани подаци x, H је ентропија и DKL је Кулбак-Лајблер дивергенција.
Онда се кораци ЕМ алгоритма могу посматрати као:
- Корак очекивања: Изабери q да максимизујеш F:
- Корак максимизације: Изабери θ да максимизујеш F:
Пример[уреди | уреди извор]
Гаусова расподела[уреди | уреди извор]
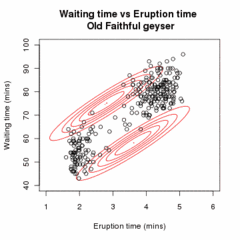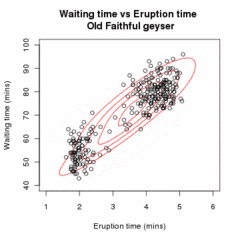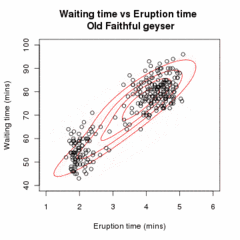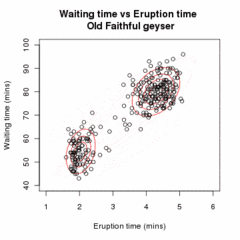
Нека је x = (x1,x2,…,xn) пример од n независних опсервација из расподеле две мултиваријационе нормалне расподеле димензије d, и нека је z=(z1,z2,…,zn) латентна варијабла којом се одређује компонента из које потиче посматрање.
- i
где је
i
Циљ је да се процене непознати параметари који представљају “мешање” вредности између Гаусових и начини и коваријансе сваког.
где је функција веродостојности:
где је индикатор функције, а f је расподела вероватноће од више варијанта. Ово може бити преписано фамилији експоненцијалних форми:
Да би се видела последња једнакост, имајте на уму да за свако i сви индикатори су једнаки нули, осим једног који је једнак један. Унутрашња сума се на тај начин смањује на један члан.
Корак Е[уреди | уреди извор]
Тренутна процена параметара θ(t) условна расподела Zi је детерминисана са Бајесовом теоремом, да буде пропорционалне висине од нормалне расподеле вероватноће, са тежином τ:
- .
Резултат Е корака у функцији:
Да бисмо видели последњу једнакост, имајте на уму да смо сумирањем по свим могућим вредностима од z где је вероватноћа сваког z производ . Сада погледајмо коефицијенте сваког члана унутар суме за.. Биће два члана and . Будући да термин у загради маргинализује по свим могућим случајевима кад , је једнако 1. Тако су коефицијенти сваког члана и који теже једнакости.
Корак М[уреди | уреди извор]
Квадратни облик Q(θ|θ(t)) значи да одређивање максималне вредности θ је релативно једноставно. Имајте на уму да τ, (μ1,Σ1) и (μ2,Σ2) могу бити све маскимизовано независно једни од других, јер се сви они појављују у одвојеним линеарним члановима. За почетак, узмимо у обзир τ, које има ограничење τ1 + τ2=1:
Ово има исти облик као МЛЕ за биномну расподелу, тако да:
У наредним проценама (μ1,Σ1):
Ово има исту форму као и тежак МЛЕ за нормалну расподелу, тако да
- and
и, преко симетрије:
- and .
Референце[уреди | уреди извор]
- ^ Dempster, A.P.; Laird, N.M.; Rubin, D.B. (1977). „Maximum Likelihood from Incomplete Data via the EM Algorithm”. Journal of the Royal Statistical Society, Series B. 39 (1): 1—38. JSTOR 2984875. MR 0501537.
- ^ Sundberg, Rolf (1974). „Maximum likelihood theory for incomplete data from an exponential family”. Scandinavian Journal of Statistics. 1 (2): 49—58. JSTOR 4615553. MR 381110.
- ^ Rolf Sundberg. 1971. Maximum likelihood theory and applications for distributions generated when observing a function of an exponential family variable. Dissertation, Institute for Mathematical Statistics, Stockholm University.
- ^ Sundberg, Rolf (1976). „An iterative method for solution of the likelihood equations for incomplete data from exponential families”. Communications in Statistics – Simulation and Computation. 5 (1): 55—64. MR 443190. doi:10.1080/03610917608812007.
Литература[уреди | уреди извор]
- Robert Hogg, Joseph McKean and Allen Craig. Introduction to Mathematical Statistics. pp. 359-364. Upper Saddle River, NJ: Pearson Prentice Hall, 2005.
- The on-line textbook: Information Theory, Inference, and Learning Algorithms, by David J.C. MacKay includes simple examples of the EM algorithm such as clustering using the soft k-means algorithm, and emphasizes the variational view of the EM algorithm, as described in Chapter 33.7 of version 7.2 (fourth edition).
- Theory and Use of the EM Method by M. R. Gupta and Y. Chen is a well-written short book on EM, including detailed derivation of EM for GMMs, HMMs, and Dirichlet.
- Bilmes, Jeff. „A Gentle Tutorial of the EM Algorithm and its Application to Parameter Estimation for Gaussian Mixture and Hidden Markov Models”. CiteSeerX 10.1.1.28.613
 , includes a simplified derivation of the EM equations for Gaussian Mixtures and Gaussian Mixture Hidden Markov Models.
, includes a simplified derivation of the EM equations for Gaussian Mixtures and Gaussian Mixture Hidden Markov Models. - Variational Algorithms for Approximate Bayesian Inference, by M. J. Beal includes comparisons of EM to Variational Bayesian EM and derivations of several models including Variational Bayesian HMMs (chapters).
- Dellaert, Frank. „The Expectation Maximization Algorithm”. CiteSeerX 10.1.1.9.9735
 , gives an easier explanation of EM algorithm in terms of lowerbound maximization.
, gives an easier explanation of EM algorithm in terms of lowerbound maximization. - The Expectation Maximization Algorithm: A short tutorial, A self-contained derivation of the EM Algorithm by Sean Borman.
- The EM Algorithm, by Xiaojin Zhu.
- Roche, Alexis (2011). „EM algorithm and variants: an informal tutorial”. arXiv:1105.1476
 .
. - Bishop, Christopher M. (2006). Pattern Recognition and Machine Learning. Springer. ISBN 978-0-387-31073-2.
- Einicke, G.A. (2012). Smoothing, Filtering and Prediction: Estimating the Past, Present and Future. Rijeka, Croatia: Intech. ISBN 978-953-307-752-9.
Спољашње везе[уреди | уреди извор]
- Various 1D, 2D and 3D demonstrations of EM together with Mixture Modeling are provided as part of the paired SOCR activities and applets. These applets and activities show empirically the properties of the EM algorithm for parameter estimation in diverse settings.
- Class hierarchy in C++ (GPL) including Gaussian Mixtures
- Fast and clean C implementation of the Expectation Maximization (EM) algorithm for estimating Gaussian Mixture Models (GMMs).







![{\displaystyle Q({\boldsymbol {\theta }}|{\boldsymbol {\theta }}^{(t)})=\operatorname {E} _{\mathbf {Z} |\mathbf {X} ,{\boldsymbol {\theta }}^{(t)}}\left[\log L({\boldsymbol {\theta }};\mathbf {X} ,\mathbf {Z} )\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/156a3df0c2afd170165c3166debd4b09f1e8f01e)















![{\displaystyle F(q,\theta )=\operatorname {E} _{q}[\log L(\theta ;x,Z)]+H(q)=-D_{\mathrm {KL} }{\big (}q{\big \|}p_{Z|X}(\cdot |x;\theta ){\big )}+\log L(\theta ;x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c79f28ad1fef1296ec1cff9f58fe24e0f5e3d83)









![{\displaystyle L(\theta ;\mathbf {x} ,\mathbf {z} )=\exp \left\{\sum _{i=1}^{n}\sum _{j=1}^{2}\mathbb {I} (z_{i}=j){\big [}\log \tau _{j}-{\tfrac {1}{2}}\log |\Sigma _{j}|-{\tfrac {1}{2}}(\mathbf {x} _{i}-{\boldsymbol {\mu }}_{j})^{\top }\Sigma _{j}^{-1}(\mathbf {x} _{i}-{\boldsymbol {\mu }}_{j})-{\tfrac {d}{2}}\log(2\pi ){\big ]}\right\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a8e067d27d7a13e113f6ae490f0e63270b819ac)


![{\displaystyle {\begin{aligned}Q(\theta |\theta ^{(t)})&=\operatorname {E} [\log L(\theta ;\mathbf {x} ,\mathbf {Z} )]\\&=\sum _{i=1}^{n}\sum _{j=1}^{2}T_{j,i}^{(t)}{\big [}\log \tau _{j}-{\tfrac {1}{2}}\log |\Sigma _{j}|-{\tfrac {1}{2}}(\mathbf {x} _{i}-{\boldsymbol {\mu }}_{j})^{\top }\Sigma _{j}^{-1}(\mathbf {x} _{i}-{\boldsymbol {\mu }}_{j})-{\tfrac {d}{2}}\log(2\pi ){\big ]}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e9e63d7397c285b53fd48bf2b81fd905b41030f)







![{\displaystyle {\begin{aligned}{\boldsymbol {\tau }}^{(t+1)}&={\underset {\boldsymbol {\tau }}{\operatorname {arg\,max} }}\ Q(\theta |\theta ^{(t)})\\&={\underset {\boldsymbol {\tau }}{\operatorname {arg\,max} }}\ \left\{\left[\sum _{i=1}^{n}T_{1,i}^{(t)}\right]\log \tau _{1}+\left[\sum _{i=1}^{n}T_{2,i}^{(t)}\right]\log \tau _{2}\right\}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e33a45f0e2590812a2187f95bb704a9290be4978)





