Стеинхаус-Јохнсон-Троттер алгоритам

Хамилтонов пут (енгл. Хамилтониан патх) у Кејлијевом графу (енгл. Цаyлеy грапх) симетричне групе генерисане Стеинхаус–Јохнсон–Троттер алгоритмом

Стеинхаус–Јохнсон–Троттер алгоритам или Јохнсон–Троттер алгоритам (енгл. Стеинхаус–Јохнсон–Троттер алгоритхм) је алгоритам који је добио име по Хугу Штајнхаусу, Селмеру M. Џонсону и Халеу Ф. Тротеру који генерише све пермутације од н елемената. Свака пермутација у низу се разликује од претходне по томе што су јој нека два суседна елемента заменила места. Овај алгоритам такође проналази Хамилтонов пут у пермутоедру (енгл. Пермутохедрон).

Ова метода је још у 17. веку била позната енглеским звонарима (енгл. цханге рингинг), а Седгеwицк 1977 ју је назвао "вероватно најистакнутијим алгоритмом за генерисање пермутација". Осим што је једноставан и рачунски ефикасан, овај алгоритам има предност у томе што се израчунавање сваке следеће пермутације може убрзати због велике сличности између узастопних пермутација.

Рекурзивна структура

Низ пермутација н бројева се може конструисати од низа пермутација н - 1 бројева тако што се број н ставља на сваку могућу позицију у свакој од краћих пермутација. Ако је пермутација од н - 1 елемената парна пермутација(енгл. паритy оф а пермутатион) (што важи за прву, трећу итд. пермутацију у низу) онда се број н поставља на сваку могућу позицију у опадајућем поретку у тој пермутацији, од н до 1. Када је пермутација од н - 1 елемената непарна, број н се поставља на сваку могућу позицију у растућем поретку.

Дакле, код пермутације од једног елемента,

1

број 2 ћемо поставити на сваку могућу позицију у опадајућем поретку и тако формирати две пермутације од два елемента,

1 2

2 1

Након тога број 3 можемо поставити на сваку могућу позицију у опадајућем поретку у првој пермутацији "1 2", и у растућем поретку у пермутацији "2 1":

1 2 3

1 3 2

3 1 2

3 2 1

2 3 1

2 1 3

У следећем кораку рекурзије, број 4 ће бити постављан у опадајућем поретку у пермутацију 1 2 3, у растућем поретку у пермутацију 1 3 2, у опадајућем поретку у пермутацију 3 1 2, итд. Исти начин постављања елемента н, наизменично растући и опадајући, се примењује за сваки број већи од н. Овим се добија да се свака пермутација разликује од претходне или померањем н-а за једну позицију или по промени два мања броја наслеђена из краће пермутације. У сваком случају, ова разлика у ствари представља само замену два суседна елемента. Када је н > 1, прва и последња пермутација у низу се такође разликују само на два суседна места, што се може доказати индукцијом.

Иако се пермутације могу генерисати рекурзивним алгоритмом који најпре формира низ мањих пермутација а затим извршава сва могућа убацивања највећег броја на рекурзиван начин, Стеинхаус-Јохнсон-Троттер алгоритам избегава рекурзију и формира низ пермутација итеративном методом.

Алгоритам

Како је то описао Јохнсон 1963, овај алгоритам за генерисање следеће пермутације од задате пермутације π, извршава следеће кораке:

• За свако и од 1 до н, нека је x_и позиција где је вредност и смештена у пермутацији π. Ако низ бројева од 1 до и - 1 у пермутацији π дефинише парну пермутацију онда је y_и = x_и - 1, а инаце y_и = x_и + 1.

• Проналази се највећи број и за који y_и представља валидну позицију у пермутацији π која садржи број мањи од и. Заменити вредности на позицијама x_и и y_и.

Ако није могуће пронаци број и такав да буде задовољен услов другог корака, алгоритам је дошао до последње пермутације у низу и престаје са радом. Ова процедура се може обавити у времену О(н) по пермутацији.

Троттер 1962 је дао алтернативну имплементацију итеративног алгоритма за исти низ пермутација у некоментарисаном псеудокоду (енгл. псеудоцоде).

Пошто ова метода генерише пермутације које су наизменично парне и непарне, она се може лако изменити тако да генерише само парне или само непарне пермутације: за генерисање следеће пермутације исте парности, треба применити исту процедуру два пута.

Евен-ово убрзање

Побољшање које је увео Схимон Евен смањује брзину извршавања алгоритма тако што чува додатне информације о сваком елементу у пермутацији: његову позицију и смер (позитиван, негативан или нула) у коме се тренутно креће (то је суштински иста информација у поређењу са парношћу пермутације у верзији алгоритма коју је дефинисао Јохнсон). Иницијално, смер броја 1 је нула, а сви остали елементи имају негативан смер:

1 -2 -3

У сваком кораку, алгоритам проналази највећи елемент чији је смер различит од нуле и замењује му место са суседним елементом у смеру у коме показује:

1 -3 -2

Ако овај корак доведе до тога да се текући елемент нађе на првој или последњој позицији у пермутацији, или ако је суседни елемент у истом смеру већи од текућег елемента, његов смер се поставља на нулу:

3 1 -2

После сваког корака, сви елементи већи од текућег имају позитивне или негативне смерове, у зависности од тога да ли се налазе између текућег елемента и почетка пермутације (позитиван) или између текућег елемента и краја пермутације (негативан). Дакле, у овом примеру, након померања броја 2, броју 3 бива поново додељен смер:

+3 2 1

Преостала два корака алгоритма за н = 3 су:

2 +3 1

2 1 3

Алгоритам престаје са радом када сви елементи постану неозначени.

Овај алгоритам се извршава за О(и) времена за сваки корак у коме је највећи број за померање н - и + 1. Према томе, замене које се врше над бројем н трају константно време. Пошто ове замене чине тек 1/н-ти део свих замена које изврши алгоритам, просечно време по пермутацији је такође константно, иако ће мали број пермутација коштати више времена.

Комплекснија верзија овог алгоритма која не садржи петље (енгл. лооплесс алгоритхм) омогућава да се генерисање сваке појединачне пермутације извршава у константном времену, али модификације потребне да се елиминишу петље га чине споријим у пракси.

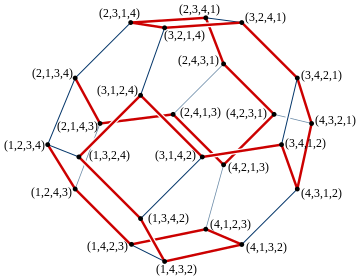
Геометријска репрезентација

Скуп свих пермутација н елемената геометријски се може представити помоћу пермутоедра, политопа (енгл. полyтопе) формираног из конвексних омотача н! вектора, пермутација вектора (1,2,...н). Иако је дефинисано у н-димензионом простору, заправо је (н - 1)-димензиони политоп; на пример пермутоедар са 4 елемената је тродимензиони полиедар, окрњени октаедар (енгл. трунцатед оцтахедрон). Ако је свако теме пермутоедра означено инверзном пермутацијом пермутацији дефинисаној од стране координата темена, добијено означавање описује Кејлијев граф симетричне групе пермутација н елемената, као што је генерисано од стране пермутација које мењају суседне парове елемената. Сваке две узастопне пермутације у низу генерисаном Стеинхаус-Јохнсон-Троттер алгоритмом одговарају на овај начин двома теменима који формирају завршне тачке ивице у пермутоедру и цео низ пермутација описује Хамилтонов пут у пермутоедру, пут који сваким теменом пролази тачно једном. Уколико је низ пермутација завршен додавањем још једне ивице из последње пермутације у прву у низу, резултат је Хамилтонов циклус.

Веза са Грејовим кодом

Грејов код (Граy цоде) за бројеве у датој основи је низ који садржи бројеве до одређене границе, тако да се парови узастопних бројева разликују за тачно једну цифру. н! пермутација н бројева од 1 до н може да се доведе у један на један представљање са н! бројева од 0 до н! - 1 тако што се свака пермутација упарује са секвенцом бројева ц_и који броји број позиција у пермутацији које су десно од вредности и и које садрже вредности мање од и (тј, број инверзија где је и веће од друге вредности) и интерпретирање ових низова бројева у факторијелном бројевном систему (енгл. фацториал нумбер сyстем). На пример пермутација (3,1,4,5,2) даје вредности ц₁ = 0, ц₂ = 0, ц₃ = 2, ц₄ = 1, ц₅ = 1. Низ (0,0,2,1,1) даје број

0 × 0! + 0 × 1! + 2 × 2! + 1 × 3! + 1 × 4! = 34.

Узастопне пермутације у низу генерисане Стеинхаус-Јохнсон-Троттер алгоритмом имају број инверзија које се разликују за једну цифру, формирајући Грејов код за факторијелни бројевни систем.

Уопштено, истраживачи комбинаторних алгоритама су дефинисали Грејов код за скуп комбинаторних објеката где су објекти поређани један до другог тако да се разликују на најмањи могући начин. У овом генерализованом случају Стеинхаус-Јохнсон-Троттер алгоритам генерише Грејов код за саме пермутације.

Историјат

Алгоритам је назван по Хуго Стеинхаус, Селмер M. Јохнсон и Хале Ф. Троттер. Џонсон и Тротер су независно један од другог осмислили алгоритам у раним шездесетим. Штајхаусова књига, првобитно објављена 1958, а на енглески преведена 1963. описује повезану слагалицу генерисања свих пермутација помоћу система честица, где се свака честица креће константном брзином дуж линије и где једна честица преузима место друге. Није могуће решење за н > 3, пошто је број замена далеко мањи од броја пермутација, али Стеинхаус-Јохнсон-Троттер алгоритам описује кретање честица са неконстантном брзином која генерише све пермутације.

Изван математике, исти метод је познат много дуже за промену звоњаве црквених звона: метод описује поступак по коме скуп црквених звона звони по свим могућим пермутацијама, мењајући редослед само два звона по промени. Ове такозване једноставне промене су забележене 1621. за 4 звона, а касније је Фабијан Стедман (Фабиан Стедман) у својој књизи излистао решења за до 6 звона. У скорије време, поштује се правило да ниједно звоно не може да остане у истој позицији три узастопне пермутације; ово правило је прекршено од стране једноставних промена, тако да су осмишљене нове стратегије које мењају више звона одједном.

Референце

• Дерсхоwитз, Нацхум (1975), „А симплифиед лооп-фрее алгоритхм фор генератинг пермутатионс”, Нордиск Тидскр. Информатионсбехандлинг (БИТ), 15 (2): 158—164, дои:10.1007/бф01932689 .
• Дијкстра, Едсгер W. (1976), „Он а гаунтлет тхроwн бy Давид Гриес” (ПДФ), Ацта Информатица, 6 (4): 357—359, дои:10.1007/БФ00268136 . Алтхоугх ДИјкстра доес нот ците анy приор литературе, ан еарлиер драфт ЕWД502 ревеалс тхат хе кнеw оф Троттер 1962.
• Ехрлицх, Гидеон (1973), „Лооплесс алгоритхмс фор генератинг пермутатионс, цомбинатионс, анд отхер цомбинаториал цонфигуратионс”, Јоурнал оф тхе АЦМ, 20 (3): 500—513, дои:10.1145/321765.321781 .
• Евен, Схимон (1973), Алгоритхмиц цомбинаторицс, Мацмиллан .
• Јохнсон, Селмер M. (1963), „Генератион оф пермутатионс бy адјацент транспоситион”, Матхематицс оф Цомпутатион, 17: 282—285, ЈСТОР 2003846, дои:10.1090/С0025-5718-1963-0159764-2 .
• Кнутх, Доналд (2011), „Сецтион 7.2.1.2: Генератинг Алл Пермутатионс”, Тхе Арт оф Цомпутер Программинг, волуме 4А, Архивирано из оригинала 30. 03. 2012. г., Приступљено 01. 06. 2015 .
• МцГуире, Гарy (2003), Беллс, мотелс анд пермутатион гроупс, ЦитеСеерX: 10.1.1.6.5544 .
• Саваге, Царла (1997), „А сурвеy оф цомбинаториал Граy цодес”, СИАМ Ревиеw, 39 (4): 605—629, ЈСТОР 2132693, дои:10.1137/С0036144595295272 .
• Седгеwицк, Роберт (1977), „Пермутатион генератион метходс”, АЦМ Цомпут. Сурв., 9 (2): 137—164, дои:10.1145/356689.356692 .
• Стеинхаус, Хуго (1964), Оне хундред проблемс ин елементарy матхематицс, Неw Yорк: Басиц Боокс, стр. 49—50 .
• Троттер, Х. Ф. (август 1962), „Алгоритхм 115: Перм”, Цоммуницатионс оф тхе АЦМ, 5 (8): 434—435, дои:10.1145/368637.368660 .

Спољашње везе

• Цоунтинг Анд Листинг Алл Пермутатионс: Јохнсон–Троттер Метход ат цут-тхе-кнот
• Референце Јава имплементатион оф ан итератор имплеметинг тхе Евенс' спеедуп алгоритхм ат соурцефорге