Komutativni dijagram

U matematici, i posebno u teoriji kategorija, komutativni dijagram je takav dijagram da svi usmereni putevi u dijagramu sa istim početnim i krajnjim tačkama vode do istog rezultata.[1] Komutativni dijagrami igraju ulogu u teoriji kategorija ekvivalentnu ulozi jednačina u algebri.[2]
Opis
[uredi | uredi izvor]Komutativni dijagram je obično sastoji od tri dela:
- objekti (takođe poznati kao temena)
- morfizmi (takođe poznati kao strelice ili ivice)
- putevi ili kompoziti
Simboli strelica
[uredi | uredi izvor]U algebarskim tekstovima, tip morfizma može da bude obeležen upotrebom različitih strelica:
- Monomorfizam (injektivni homomorfizam) može da bude obeležen sa .[3]
- Epimorfizam (surjektivni homomorfizam) može da bude obeležen sa .
- Izomorfizam (bijektivni homomorfizam) može da bude obeležen sa .
- Isprekidana strelica tipično predstavlja tvrdnju da označeni morfizam postoji (šta god da ostatak dijagrama sadrži); strelica može opciono da bude obeležena kao .
- Ako je morfizam adiciono jedinstven, onda isprekidana linija može da bude obeležena sa ili .
Ove konvencije su obično dovoljne, tako da tekst uglavnom ne objašnjava značenje različitih tipova strelica.
Provera komutativnosti
[uredi | uredi izvor]Kommutativnost ima smisla za poligon bilo kog konačnog broja strana (uključujući samo 1 ili 2), a dijagram je komutativan ako je svaki poligonalni potdijagram komutativan. Treba imati na umu da dijagram može biti nekomutativan, tj. sastav različitih putanja u dijagramu možda neće dati isti rezultat.
Primeri
[uredi | uredi izvor]U levom dijagramu, koji izražava prvu teoremu izomorfizma, komutativnost trougla znači da je . U desnom dijagramu komutativnost kvadrata znači .

|

|
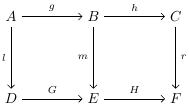
Da bi dijagram ispod bio komutativan, moraju biti zadovoljene tri jednakosti:
Ovde, pošto prva jednakost sledi iz zadnje dve, dovoljno je pokazati da su (2) i (3) istinite da bi dijagram bio komutativan. Međutim, pošto jednakost (3) generalno ne proizilazi iz druge dve, u opštem slučaju nije dovoljno imati samo jednakosti (1) i (2) da bi se pokazalo da je dijagram komutativan.
|
Praćenje dijagrama
[uredi | uredi izvor]Praćenje dijagrama (koja se takođe naziva dijagramskom pretragom) je metoda matematičkog dokaza koja se naročito koristi u homološkoj algebri, gde se uspostavlja svojstvo nekog morfizma pronalazeći elemente komutativnog dijagrama.[4] Dokaz pomoću dijagrama obično uključuje formalnu upotrebu svojstava dijagrama, kao što su injektivne ili surjektivne mape, ili tačne sekvence.[5] Konstruiše se silogizam za koji je grafički prikaz dijagrama samo vizuelno pomagalo. Iz toga sledi da se vrši „pretraga” elemenata na dijagramu, sve dok se ne konstruiše ili potvrdi željeni element ili rezultat.
Primeri dokaza pomoću dijagramskog praćenja uključuju one koji se obično daju za pet lema, zmijsku lemu, zig-zag lemu, i devet lema.
U višoj teoriji kategorija
[uredi | uredi izvor]U višoj teoriji kategorija, ne razmatraju se samo objekti i strelice, već strelice između strelica, strelice između strelica koje su između strelica, i tako dalje ad infinitum. Na primer, kategorija malih kategorija Mačka je prirodno 2-kategorija, sa funkorima kao njenim strelicama, i prirodnim transformacijama kao strelicama između funktora. U tom okruženju, komutativni dijagrami mogu takođe da sadrže i ove više strelice, koje su često prikazuju u sledećem stilu: . Na primer, sledeći (pomalo trivijalni) dijagram prikazuje dve kategorije C i D, zajedno sa dva funktora F, G : C → D i prirodnom transformacijom α : F ⇒ G:
Postoje dve vrste kompozicija u 2-kategoriji (koje se nazivaju vertikalna kompozicija i horizontalna kompozicija), a mogu se prikazati i pomoću dijagrama spajanja (pgledajte na primer definiciju 2-kategorije).
Dijagrami kao funktori
[uredi | uredi izvor]Komutativni dijagram u kategoriji C može se tumačiti kao funktor iz indeksne kategorije J do C; ovaj funktor se naziva dijagram.
Formalnije, komutativni dijagram je vizualizacija dijagrama indeksiranog po parcijalno uređenoj kategoriji. Takav dijagram obično uključuje:
- čvor za svaki objekt iz indeksne kategorije,
- strelicu za generisanje skupa morfizama (izostavljajući mape identiteta i morfizme koji se mogu izraziti kao kompozicije),
- komutativnost dijagrama (jednakost različitih kompozicija mapa između dva objekta), što odgovara jedinstvenosti mape između dva objekta u parcijalno uređenoj kategoriji.
Nasuprot tome, dati komutativni dijagram definiše parcijalno uređenu kategoriju, gde su:
- objekti čvorovi,
- postoji morfizam između bilo koja dva objekta ako i samo ako postoji (usmereni) put između čvorova,
- sa odnosom da je ovaj morfizam jedinstven (bilo koji sastav mapa je definisan njegovom domenom i ciljem: ovo je aksiom komutativnosti).
Međutim, nije svaki dijagram komutativan (pojam dijagrama strogo generalizuje komutativni dijagram). Jednostavan primer je dijagram jednog objekta sa endomorfizmom (), ili sa dve paralelne strelice (, to jest, , što se ponekad naziva i slobodno treperenje), kao što se koristi u definiciji ekvilajzera, ne mora da bude komutativan. Dalje, dijagrami mogu biti zbrkani ili se može desiti da ih je nemoguće nacrtati, kada je broj objekata ili morfizama velik (ili čak beskonačan).
Vidi još
[uredi | uredi izvor]Reference
[uredi | uredi izvor]- ^ Weisstein, Eric W. „Commutative Diagram”. mathworld.wolfram.com (на језику: енглески). Приступљено 25. 11. 2019.
- ^ Barr & Wells (2002, Section 1.7))
- ^ „Maths - Category Theory - Arrow - Martin Baker”. www.euclideanspace.com. Приступљено 25. 11. 2019.
- ^ „The Definitive Glossary of Higher Mathematical Jargon — Chasing”. Math Vault (на језику: енглески). 1. 8. 2019. Приступљено 25. 11. 2019.
- ^ Weisstein, Eric W. „Diagram Chasing”. mathworld.wolfram.com (на језику: енглески). Приступљено 25. 11. 2019.
Literatura
[uredi | uredi izvor]- Adámek, Jiří; Horst Herrlich; George E. Strecker (1990), Abstract and Concrete Categories (PDF), John Wiley & Sons, ISBN 0-471-60922-6, Архивирано из оригинала (PDF) 21. 04. 2015. г., Приступљено 18. 02. 2020 Now available as free on-line edition (4.2MB PDF).
- Barker-Plummer, Dave; Bailin, Sidney C. (1997). „The Role of Diagrams in Mathematical Proofs”. Machine Graphics and Vision. 6 (1): 25—56. 10
.1 .1 .49 .4712. (Special Issue on Diagrammatic Representation and Reasoning). - Barker-Plummer, Dave; Bailin, Sidney C. (2001). „On the practical semantics of mathematical diagrams”. Ур.: Anderson, M. Reasoning with Diagrammatic Representations. Springer Verlag. ISBN 978-1-85233-242-6. CiteSeerX: 10
.1 .1 .30 .9246. - Kidman, G. (2002). „The Accuracy of mathematical diagrams in curriculum materials”. Ур.: Cockburn, A.; Nardi, E. Proceedings of the PME 26. 3. University of East Anglia. стр. 201—8.
- Kulpa, Zenon (2004). „On Diagrammatic Representation of Mathematical Knowledge”. Ур.: Andréa Asperti; Bancerek, Grzegorz; Trybulec, Andrzej. Mathematical knowledge management: third international conference, MKM 2004, Białowieża, Poland, September 19–21, 2004 : Proceedings. Springer. стр. 191—204. ISBN 978-3-540-23029-8.
- Puphaiboon, K.; Woodcock, A.; Scrivener, S. (25. 3. 2005). „Design method for developing mathematical diagrams”. Ур.: Bust, Philip D.; McCabe, P.T. Contemporary ergonomics 2005 Proceedings of the International Conference on Contemporary Ergonomics (CE2005). Taylor & Francis. ISBN 978-0-415-37448-4.
- Barr, Michael; Wells, Charles (2012), Category Theory for Computing Science, Reprints in Theory and Applications of Categories, 22 (3rd изд.), Архивирано из оригинала 15. 1. 2015. г., Приступљено 12. 10. 2012 Revised and corrected free online version of Grundlehren der mathematischen Wissenschaften (278) Springer-Verlag, 1983).
- Barr, Michael; Wells, Charles (2005), Toposes, Triples and Theories, Reprints in Theory and Applications of Categories, 12 (revised изд.), MR 2178101.
- Borceux, Francis (1994). Handbook of categorical algebra. Encyclopedia of Mathematics and its Applications 50–52. Cambridge University Press.
- Freyd, Peter J. (1964). Abelian Categories. New York: Harper and Row.
- Freyd, Peter J.; Scedrov, Andre (1990). Categories, allegories. North Holland Mathematical Library. 39. North Holland. ISBN 978-0-08-088701-2.
- Goldblatt, Robert (2006) [1979]. Topoi: The Categorial Analysis of Logic. Studies in logic and the foundations of mathematics. 94 (Reprint, revised изд.). Dover Publications. ISBN 978-0-486-45026-1.
- Herrlich, Horst; Strecker, George E. (2007). Category Theory (3rd изд.). Heldermann Verlag Berlin. ISBN 978-3-88538-001-6..
- Kashiwara, Masaki; Schapira, Pierre (2006). Categories and Sheaves. Grundlehren der Mathematischen Wissenschaften. 332. Springer. ISBN 978-3-540-27949-5.
- Lawvere, F. William; Rosebrugh, Robert (2003). Sets for Mathematics. Cambridge University Press. ISBN 978-0-521-01060-3.
- Lawvere, F. W.; Schanuel, Stephen Hoel (2009) [1997]. Conceptual Mathematics: A First Introduction to Categories (2nd изд.). Cambridge University Press. ISBN 978-0-521-89485-2.
- Leinster, Tom (2004). Higher Operads, Higher Categories. Higher Operads. London Math. Society Lecture Note Series. 298. Cambridge University Press. стр. 448. Bibcode:2004hohc.book.....L. ISBN 978-0-521-53215-0. Архивирано из оригинала 25. 10. 2003. г. Приступљено 3. 4. 2006.
- Leinster, Tom (2014). Basic Category Theory. Cambridge University Press. Bibcode:2016arXiv161209375L.
- Lurie, Jacob (2009). Higher Topos Theory. Annals of Mathematics Studies. 170. Princeton, NJ: Princeton University Press. ISBN 978-0-691-14049-0. MR 2522659. arXiv:math.CT/0608040
 .
. - Mac Lane, Saunders (1998). Categories for the Working Mathematician. Graduate Texts in Mathematics. 5 (2nd изд.). Springer-Verlag. ISBN 978-0-387-98403-2. MR 1712872.
- Mac Lane, Saunders; Birkhoff, Garrett (1999) [1967]. Algebra (2nd изд.). Chelsea. ISBN 978-0-8218-1646-2.
- Martini, A.; Ehrig, H.; Nunes, D. (1996). „Elements of basic category theory”. Technical Report. 96 (5).
- May, Peter (1999). A Concise Course in Algebraic Topology. University of Chicago Press. ISBN 978-0-226-51183-2.
- Guerino, Mazzola (2002). The Topos of Music, Geometric Logic of Concepts, Theory, and Performance. Birkhäuser. ISBN 978-3-7643-5731-3.
- Pedicchio, Maria Cristina; Tholen, Walter, ур. (2004). Categorical foundations. Special topics in order, topology, algebra, and sheaf theory. Encyclopedia of Mathematics and Its Applications. 97. Cambridge: Cambridge University Press. ISBN 978-0-521-83414-8. Zbl 1034.18001.
- Pierce, Benjamin C. (1991). Basic Category Theory for Computer Scientists. MIT Press. ISBN 978-0-262-66071-6.
- Schalk, A.; Simmons, H. (2005). An introduction to Category Theory in four easy movements (PDF). Архивирано из оригинала (PDF) 21. 3. 2017. г. Приступљено 19. 2. 2020. Notes for a course offered as part of the MSc. in Mathematical Logic, Manchester University.
- Simpson, Carlos (2010). Homotopy theory of higher categories. Bibcode:2010arXiv1001.4071S. arXiv:1001.4071
 ., draft of a book.
., draft of a book. - Taylor, Paul (1999). Practical Foundations of Mathematics. Cambridge Studies in Advanced Mathematics. 59. Cambridge University Press. ISBN 978-0-521-63107-5.
- Turi, Daniele (1996—2001). „Category Theory Lecture Notes” (PDF). Приступљено 11. 12. 2009. Based on Mac Lane 1998.
- Jean-Pierre Marquis (2008). From a Geometrical Point of View: A Study of the History and Philosophy of Category Theory. Springer Science & Business Media. ISBN 978-1-4020-9384-5.
Spoljašnje veze
[uredi | uredi izvor]- Diagram Chasing at MathWorld
- WildCats is a category theory package for Mathematica. Manipulation and visualization of objects, morphisms, categories, functors, natural transformations.
- „Diagrams”. The Stanford Encyclopedia of Philosophy. jesen 2008.
- Kulpa, Zenon. „Diagrammatics: The art of thinking with diagrams”. Архивирано из оригинала 25. 4. 2013. г.
- One of the oldest extant diagrams from Euclid by Otto Neugebauer
- Lomas, Dennis (1998). „Diagrams in Mathematical Education: A Philosophical Appraisal”. Philosophy of Education Society. Архивирано из оригинала 2011. г.
















