Апсолутна вредност

График функције апсолутне вредности

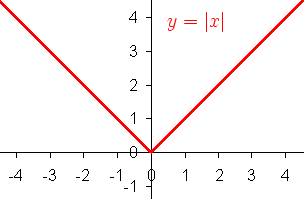
У математици, апсолутна вредност (или модуо) реалног броја је његова нумеричка вредност не узимајући у обзир знак тог броја.

Нпр. бројеви 3 и −3 имају апсолутну вредност 3, апсолутна вредност броја 5 је 5, броја −4 је 4, док је 0 апсолутна вредност само за број 0.

Дефиниција

За било који реалан број a, апсолутна вредност, означава се |a|, је једнака броју a ако је a ≥ 0, и −a ако је a < 0. $|a|=\left\{{\begin{matrix}a,&a\geq 0\\-a,&a<0\end{matrix}}\right.$

|a| не може бити негативан број јер је апсолутна вредност увек или позитиван број или 0. Другим речима, неједначина |a| < 0 нема решења. Такође, не мора важити |−a| = a, пошто a може бити негативно.

Апсолутна вредност се може разумети као удаљеност датог броја од нуле.

Својства

Апсолутна вредност броја a има следећа својства:

1. |a| ≥ 0
2. |a| = 0 акко a = 0.
3. |ab| = |a||b|
4. |a/b| = |a| / |b| (ако је b ≠ 0)
5. |a+b| ≤ |a| + |b| (неједнакост троугла)
6. |a−b| ≥ ||a| − |b||
7. $\left|a\right|={\sqrt {a^{2}}}$
8. |a| ≤ b акко −b ≤ a ≤ b
9. |a| ≥ b акко a ≤ −b или b ≤ a

Последња два својства су корисна при решавању неједнаначина, нпр:

|x − 3| ≤ 9

−9 ≤ x−3 ≤ 9

−6 ≤ x ≤ 12.

За реалну вредност аргумента, функција f(x) = |x| је непрекидна свуда, а диференцијабилна свуда осим за x = 0. Уколико је аргумент комплексна променљива, функција је непрекидна свуда, али није нигде холоморфна (односно диференцијабилна; један начин да се то види је да се докаже да не задовољава Коши-Риманове једначине).

За комплексни број z = a + ib, дефинише се модуо комплексног броја као |z| = √(a² + b²) = √ (z z^*) (погледати квадратни корен и Конјугован комплексан број). Овако дефинисан модуо комплексног броја задовољава својства 1–6 дата изнад. Опет се модуо комплексног броја, као и за реалне бројеве, може разумети као удаљеност од координатног почетка.

Често је корисно израз |x − y| посматрати као растојање између x и y (на реалној бројевној правој уколико су x и y реални бројеви, или, пак, у комплексној равни, уколико су x и y комплексни бројеви). Коришћењем овакве дефиниције, и скуп реалних, и скуп комплексних бројева постају метрички простори.

Функција није инвертибилна јер се сваком броју a и његовом опозиту −a додељују исте вредности.

Апсолутна вредност комплексног броја

Апсолутна вредност комплексног броја (такође звана и модуо комплексног броја) $c\in \mathbb {C}$ је дата као $|c|={\sqrt {c\,{\overline {c}}}}$, где је ${\overline {c}}$ конјугована вредност броја $c$. Писањем $c$ као $c=a+b\,i$ за $a,b\in \mathbb {R}$, горња једначина се своди на $|c|={\sqrt {a^{2}+b^{2}}}$.

Апсолутна вредност вектора

Апсолутна вредност вектора v = (x₁, x₂,..., x_n) у Еуклидском простору Rⁿ дата је као

$\left|\mathbf {v} \right|={\sqrt {x_{1}^{2}+x_{2}^{2}+...+x_{n}^{2}}}$.

|v| се може сматрати дужином вектора v.

Алгоритам

У C програмском језику, abs(), labs(), llabs() (у C99), fabs(), fabsf(), и fabsl() функције рачунају апсолутну вредност њиховог аргумента. Кодирање апсолутне вредности када је аргумент цео број је лако:

int abs(int i)
{
    if (i < 0)
        return -i;
    else
        return i;
}