Bajesovo zaključivanje

Bajesovo zaključivanje je metoda statističkog zaključivanja u kojoj se Bajesova teorema koristi koristi za ažuriranje verovatnoće za hipotezu kad god više dokaza ili informacija postane dostupno. Bajesovo zaključivanje je važna tehnika u statistici, a posebno u matematičkoj statistici. Bajesovo ažuriranje je posebno važno u dinamičkoj analizi niza podataka. Bajesovo zaključivanje je našlo primenu u širokom spektru aktivnosti, uključujući nauku, inženjerstvo, filozofiju, medicinu, sport i pravo. U filozofiji teorije odlučivanja, Bajesovo zaključivanje je usko povezano sa subjektivnom verovatnoćom, koja se često naziva i „Bajesova verovatnoća”.

Uvod u Bajesovo pravilo

A geometric visualisation of Bayes' theorem. In the table, the values 2, 3, 6 and 9 give the relative weights of each corresponding condition and case. The figures denote the cells of the table involved in each metric, the probability being the fraction of each figure that is shaded. This shows that P(A|B) P(B) = P(B|A) P(A) i.e. P(A|B) = P(B|A) P(A)/P(B) . Similar reasoning can be used to show that P(Ā|B) = P(B|Ā) P(Ā)/P(B) etc.

Glavni članak: Bajesova teorema

Takođe pogledajte: Bajesova verovatnoća

Formalno objašnjenje

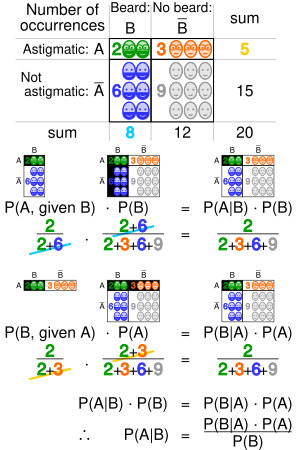
Bajesovo zaključivanje derives the posterior probability as a consequence of two antecedents: a prior probability and a "likelihood function" derived from a statistical model for the observed data. Bayesian inference computes the posterior probability according to Bayes' theorem:

$P(H\mid E)={\frac {P(E\mid H)\cdot P(H)}{P(E)}}$

where

• $\textstyle H$ stands for any hypothesis whose probability may be affected by data (called evidence below). Often there are competing hypotheses, and the task is to determine which is the most probable.
• $\textstyle P(H)$, the prior probability, is the estimate of the probability of the hypothesis $\textstyle H$ before the data $\textstyle E$, the current evidence, is observed.
• $\textstyle E$, the evidence, corresponds to new data that were not used in computing the prior probability.
• $\textstyle P(H\mid E)$, the posterior probability, is the probability of $\textstyle H$ given $\textstyle E$, i.e., after $\textstyle E$ is observed. This is what we want to know: the probability of a hypothesis given the observed evidence.
• $\textstyle P(E\mid H)$ is the probability of observing $\textstyle E$ given $\textstyle H$, and is called the likelihood. As a function of $\textstyle E$ with $\textstyle H$ fixed, it indicates the compatibility of the evidence with the given hypothesis. The likelihood function is a function of the evidence, $\textstyle E$, while the posterior probability is a function of the hypothesis, $\textstyle H$.
• $\textstyle P(E)$ is sometimes termed the marginal likelihood or "model evidence". This factor is the same for all possible hypotheses being considered (as is evident from the fact that the hypothesis $\textstyle H$ does not appear anywhere in the symbol, unlike for all the other factors), so this factor does not enter into determining the relative probabilities of different hypotheses.

For different values of $\textstyle H$, only the factors $\textstyle P(H)$ and $\textstyle P(E\mid H)$, both in the numerator, affect the value of $\textstyle P(H\mid E)$ – the posterior probability of a hypothesis is proportional to its prior probability (its inherent likeliness) and the newly acquired likelihood (its compatibility with the new observed evidence).

Bayes' rule can also be written as follows:

$P(H\mid E)={\frac {P(E\mid H)}{P(E)}}\cdot P(H)$

where the factor $\textstyle {\frac {P(E\mid H)}{P(E)}}$ can be interpreted as the impact of $E$ on the probability of $H$.

Alternatives to Bayesian updating

Bayesian updating is widely used and computationally convenient. However, it is not the only updating rule that might be considered rational.

Ian Hacking noted that traditional "Dutch book" arguments did not specify Bayesian updating: they left open the possibility that non-Bayesian updating rules could avoid Dutch books. Hacking wrote "And neither the Dutch book argument nor any other in the personalist arsenal of proofs of the probability axioms entails the dynamic assumption. Not one entails Bayesianism. So the personalist requires the dynamic assumption to be Bayesian. It is true that in consistency a personalist could abandon the Bayesian model of learning from experience. Salt could lose its savour."

Indeed, there are non-Bayesian updating rules that also avoid Dutch books (as discussed in the literature on "probability kinematics") following the publication of Richard C. Jeffrey's rule, which applies Bayes' rule to the case where the evidence itself is assigned a probability. The additional hypotheses needed to uniquely require Bayesian updating have been deemed to be substantial, complicated, and unsatisfactory.

Formalni opis Bajesovog zaključivanja

Opisi

• $x$, a data point in general. This may in fact be a vector of values.
• $\theta$, the parameter of the data point's distribution, i.e., $x\sim p(x\mid \theta )$ . This may in fact be a vector of parameters.
• $\alpha$, the hyperparameter of the parameter distribution, i.e., $\theta \sim p(\theta \mid \alpha )$ . This may in fact be a vector of hyperparameters.
• $\mathbf {X}$ is the sample, a set of $n$ observed data points, i.e., $x_{1},\ldots ,x_{n}$.
• ${\tilde {x}}$, a new data point whose distribution is to be predicted.

Literatura

• Aster, Richard; Borchers, Brian, and Thurber, Clifford (2012). Parameter Estimation and Inverse Problems, Second Edition, Elsevier. ISBN 0123850487, ISBN 978-0123850485
• Bickel, Peter J. & Doksum, Kjell A. (2001). Mathematical Statistics, Volume 1: Basic and Selected Topics (Second (updated printing 2007) изд.). Pearson Prentice–Hall. ISBN 978-0-13-850363-5. 
• Box, G. E. P. and Tiao, G. C. (1973) Bayesian Inference in Statistical Analysis, Wiley, ISBN 0-471-57428-7
• Edwards, Ward (1968). „Conservatism in Human Information Processing”. Ур.: Kleinmuntz, B. Formal Representation of Human Judgment. Wiley. 
• Edwards, Ward (1982). Daniel Kahneman; Paul Slovic; Amos Tversky, ур. „Judgment under uncertainty: Heuristics and biases”. Science. 185 (4157): 1124—1131. Bibcode:1974Sci...185.1124T. PMID 17835457. doi:10.1126/science.185.4157.1124. 
• Jaynes E. T. (2003) Probability Theory: The Logic of Science, CUP. ISBN 978-0-521-59271-0 (Link to Fragmentary Edition of March 1996).
• Howson, C. & Urbach, P. (2005). Scientific Reasoning: the Bayesian Approach (3rd изд.). Open Court Publishing Company. ISBN 978-0-8126-9578-6. 
• Phillips, L. D.; Edwards, Ward (октобар 2008). „Chapter 6: Conservatism in a Simple Probability Inference Task (Journal of Experimental Psychology (1966) 72: 346-354)”. Ур.: Jie W. Weiss; David J. Weiss. A Science of Decision Making:The Legacy of Ward Edwards. Oxford University Press. стр. 536. ISBN 978-0-19-532298-9. CS1 одржавање: Формат датума (веза)
• Vallverdu, Jordi (2016). Bayesians Versus Frequentists A Philosophical Debate on Statistical Reasoning. New York: Springer. ISBN 978-3-662-48638-2. 
• Stone, JV (2013), "Bayes’ Rule: A Tutorial Introduction to Bayesian Analysis", Download first chapter here, Sebtel Press, England.
• Dennis V. Lindley (2013). Understanding Uncertainty, Revised Edition (2nd изд.). John Wiley. ISBN 978-1-118-65012-7. 
• Colin Howson & Peter Urbach (2005). Scientific Reasoning: The Bayesian Approach (3rd изд.). Open Court Publishing Company. ISBN 978-0-8126-9578-6. 
• Berry, Donald A. (1996). Statistics: A Bayesian Perspective. Duxbury. ISBN 978-0-534-23476-8. 
• Morris H. DeGroot & Mark J. Schervish (2002). Probability and Statistics (third изд.). Addison-Wesley. ISBN 978-0-201-52488-8. 
• Bolstad, William M. (2007) Introduction to Bayesian Statistics: Second Edition, John Wiley ISBN 0-471-27020-2
• Winkler, Robert L (2003). Introduction to Bayesian Inference and Decision (2nd изд.). Probabilistic. ISBN 978-0-9647938-4-2. 
• Lee, Peter M. Bayesian Statistics: An Introduction. Fourth Edition (2012), John Wiley ISBN 978-1-1183-3257-3
• Carlin, Bradley P. & Louis, Thomas A. (2008). Bayesian Methods for Data Analysis, Third Edition. Boca Raton, FL: Chapman and Hall/CRC. ISBN 978-1-58488-697-6. 
• Gelman, Andrew; Carlin, John B.; Stern, Hal S.; Dunson, David B.; Vehtari, Aki; Rubin, Donald B. (2013). Bayesian Data Analysis, Third Edition. Chapman and Hall/CRC. ISBN 978-1-4398-4095-5. 
• Berger, James O (1985). Statistical Decision Theory and Bayesian Analysis. Springer Series in Statistics (Second изд.). Springer-Verlag. Bibcode:1985sdtb.book.....B. ISBN 978-0-387-96098-2. 
• Bernardo, José M.; Smith, Adrian F. M. (1994). Bayesian Theory. Wiley. 
• DeGroot, Morris H., Optimal Statistical Decisions. Wiley Classics Library. 2004. (Originally published (1970) by McGraw-Hill.) ISBN 0-471-68029-X.
• Schervish, Mark J. (1995). Theory of statistics. Springer-Verlag. ISBN 978-0-387-94546-0. 
• Jaynes, E. T. (1998) Probability Theory: The Logic of Science.
• O'Hagan, A. and Forster, J. (2003) Kendall's Advanced Theory of Statistics, Volume 2B: Bayesian Inference. Arnold, New York. ISBN 0-340-52922-9.
• Robert, Christian P (2001). The Bayesian Choice – A Decision-Theoretic Motivation (second изд.). Springer. ISBN 978-0-387-94296-4. 
• Glenn Shafer and Pearl, Judea, eds. (1988) Probabilistic Reasoning in Intelligent Systems, San Mateo, CA: Morgan Kaufmann.
• Pierre Bessière et al. (2013), "Bayesian Programming", CRC Press. ISBN 9781439880326
• Francisco J. Samaniego (2010), "A Comparison of the Bayesian and Frequentist Approaches to Estimation" Springer, New York, ISBN 978-1-4419-5940-9

Spoljašnje veze

• Hazewinkel Michiel, ур. (2001). „Bayesian approach to statistical problems”. Encyclopaedia of Mathematics. Springer. ISBN 978-1556080104. 
• Bayesian Statistics from Scholarpedia.
• Introduction to Bayesian probability from Queen Mary University of London
• Mathematical Notes on Bayesian Statistics and Markov Chain Monte Carlo
• Bayesian reading list, categorized and annotated by Tom Griffiths
• A. Hajek and S. Hartmann: Bayesian Epistemology, in: J. Dancy et al. (eds.), A Companion to Epistemology. Oxford: Blackwell 2010, 93-106.
• S. Hartmann and J. Sprenger: Bayesian Epistemology, in: S. Bernecker and D. Pritchard (eds.), Routledge Companion to Epistemology. London: Routledge 2010, 609-620.
• Stanford Encyclopedia of Philosophy: "Inductive Logic"
• Bayesian Confirmation Theory
• What Is Bayesian Learning?
• Data, Uncertainty and Inference An introduction to Bayesian inference and MCMC with a lot of examples fully explained. (free ebook)