Кружно растављање

Кружно растављање је метода за обављање прелиминарног смањења потенцијалних простих бројева од почетног скуп свих природних бројева 2 и већих; вероватно од доношења листе резултата потенцијалних простих бројева до Ератостеновог сита или других сита која раздвајају простих бројева из сложених, али може и додатно да се користи као прост број сито утоваривач по себи од рекурзивне примене кружног растављања генерације алгоритма. Много дефинитивно раде на кружном растављању, сита користе кружно разлагање, и круг сита, је смислио Пол Притхард[1][2][3][4] iу формулисању низа различитих алгоритама. Да би се показала употреба кружног растављања графички, један почиње да пише природне бројеве по круговима као што је приказано на дијаграму. Прости бројеви су у најужем кругу имају своје сличне позиције у другим круговима, формирајући кракове простих бројева. Умножак простих бројева у најужем кругу форми жица сложених бројева у спољашњим круговима.
Узорак графичког поступка
[уреди | уреди извор]- Пронађи првих неколико простих бројева тако да формирају основе кружног растављања. Они су познати или можда одређени из претходних апликација мањих кружних растављања или их је брзо пронађи користећи Ератостеново сито.
- Множење базних основних бројева заједно даје резултат n који је обим кружног разлагање.
- Напиши бројеве од 1 до n у круг. Ово ће бити најунутрашњији круг који представља једну кружну ротацију.
- За бројеве од 1 до n у најужем кругу, удар искљује све умношке базних простих бројева из једног корака како се примењује у кораку 2. Ова сложена елиминација броја се може постићи или употребом сито као што је Ератостеново сито или као резултат примене мањих кружних растављања.
- Узимајући да је x број кругова написаних до сада, настави са писањем xn + 1 to xn + n у концентричним круговима најудаљенијег круга, тако да xn + 1 је само позиција као и (x − 1)n + 1.
- Поновите корак 5 до највеће ротације круга који обухвата највећи број тестирања простих.
- Избрисати број 1.
- Избрисати све полуге простих бројева као у кораку 1 и применити у кораку 2 у свим спољашњим круговима, без одјаве простих бројева у најунутрашњијем кругу (у кругу 1).
- Избрисати полуге свих простих бројева избрисаних из ужег круга 1 у кораку 4 на исти начин као и брисање полуге од основних простих бројева у кораку 8.
- Преостали бројеви у кругу су углавном прости бројеви (они се колективно називају "релативно" прости бројеви). Користити друге методе као што су Ератостеново сито или даљу примену већих кружних раслојавања за уклањање преосталих не-простих бројева.
Пример
[уреди | уреди извор]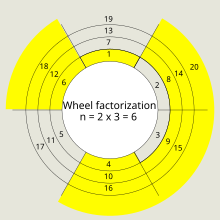
1. Наћи прво 2 проста броја: 2 и 3.
2. n = 2 × 3 = 6
3.
1 2 3 4 5 6
4. Искључити чиниоце 2 и 3 који су као и 4 и 6 чиниоци 2; 6 као једини чинилац 3 је већ погођен:
1 2 3456
5. x = 1. xn + 1 = 1 · 6 + 1 = 7. (x + 1)n = (1 + 1) · 6 = 12. Напиши од 7 до 12 са 7 усклађен са 1.
1 2 34567 8 9 10 11 12
6. x = 2. xn + 1 = 2 · 6 + 1 = 13. (x + 1)n = (2 + 1) · 6 = 18. Напиши од 13 до 18 Поновите поступак за неколико наредних редова.
1 2 34567 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
7 и 8. Просејавање
12 345678910 11 12 13141516 17 18 19202122 23 24 25262728 29 30
9. Просејавање
12 3456789101112131415161718192021222324252627282930
10. Добијена листа садржи не-прости број 25 који је 52. Користи друге методе као што је сито да би се елиминисањем дошло до
2 3 5 7 11 13 17 19 23 29
Пазити да управо помоћу следећег примарног број 5 циклуса кругова и елиминисањем вишеструког (s) простог броја (и то само простог) са листе резултата, добили смо базу круга по кораку 4 за кружно разлагање са основним простим бројевивима од 2, 3 и 5; ово је један круг унапред претходне 2/3 кружног растављања. Једном би могли да пратите кораке на корак 10 користећи следећи успех у 7 циклусу и само отклањање 7 са листе резултата у кораку 10 (остављајући неке "релативно" просте бројеве у овом случају и све узастопне случајеве - односно није истина потпуно квалификованих простих бројева), да би следећи даљи напредни круг, рекурзивно понављајући кораке неопходни су сукцесивно већи кругови.
Анализе и рачунарска имплементација
[уреди | уреди извор]Формално, метода користи следећа сазнања: прво, да је скуп основних простих уједињен са својим (бесконачно) надскуп простих бројева. Друго, да бесконачан низ може лако да се одвоји по основи између 2 и основе пара производа. (Пазити да 1 захтева посебно руковање.)
Као што се види на примеру, резултат поновљених апликација рекурзивним поступком из корака 4 до 10 може бити листа круга који обухвата било које жељено просејавање опсега (на које се може скратити) и листа резултира затим обухвата само умношке простих бројева већи од једне последње половине основних простих бројева.
Пазити да круг простире жељену горњу границу просејавања опсега, може се зауставити стварање додатних кругова и користити информације из тог круга од отпадака преосталих сложених бројева са тог списка прошлог круга помоћу Ератостеновог сита типа технике али користећи образац карактеристичан за круг да би избегле сувишне купл; неке оптимизације ће моћи да се врше на основу чињенице да (биће доказано у следећем одељку) да неће бити понављања куплинг било ког сложеног броја: сваки преостали сложени број ће се поништити тачно једаном. Алтернативно, може да настави да генерише скраћене листе лако помоћу простих бројева до квадратног корена жељеног сита, у том случају ће сваки преостали број репрезентације у кругу бити главни; Међутим, иако је овај метод ефикасан за редукцију сложених бројева више пута, он губи много времена спољно на куплинг операције у обради кругова узастопних прелаза. Елиминација сложених бројевакружног раслојавања је заснован< на следећем: За дати број k > n знамо да К није прост ако k mod n и n нису узајамно прости. Од тога, део бројева које може сито да елиминише се утврди (мада нису сви физички раскинути, а многи се могу аутоматски поништити у раду копирања мањих кругова до већим кругова) као 1 - phi (n) / n, која је и ефикасност сита
Пошто је познато[5]
где је γ Ојлерова константа, γ = 0.577215665..., e−γ = 0.56145948... . Овај phi(n) / n иде полако до нуле како се n повећава до бесконачности и може се видети да ова ефикасност расте веома споро до 100% за бесконачно велике n. Од својстава phi, то се лако може видети да је најефикасније сито мање од x је оно где је и (тј кружна генерација се може зауставити када последњи круг пролази или има довољан обим да обухвати највећи број у опсегу просејавања).
Да буду максимално коришћењи на рачунару, желимо бројеве који су мањи од n и релативно прости као скуп. Користећи неколико запажања, пар може лако бити генерисан:
- Почети са , чији пар је за са 2 као први прост број. Овај почетни скуп значи да су сви број са почетком укључени као "релативно" прости бројеви обима круга 1.
- Пратећи парове који су што значи да почиње са 3 за све непарне бројеве са чиниоцима 2 отклоњен (обим 2), је чинилац 2. и 3. елиминисани (обим 6) као полазна основа за точак у горњем примеру и тако даље.
- Пустити да буде скуп у којем је к додат сваком елементу .
- Тадагде представља операцију уклањања свих множилаца x.
- 1 и биће два најмања броја скупа када је отклања потребу за рачунање простих бројева одвојено иако алгоритам не треба да води евиденцију о свим отклоњеним основним простим бројевима који више нису укључени у наредним парови.
- Сви парови где је обим n > 2су симетричне око , смањивањем услова складиштења. Следећи алгоритам не користи ову чињеницу, али је заснован на чињеници да су разлике између узастопних бројева у сваком пару симетричне око пола пута тачке.
Види још
[уреди | уреди извор]Референце
[уреди | уреди извор]- ^ Pritchard, Paul, "Linear prime-number sieves: a family tree," Sci.
- ^ Paul Pritchard, A sublinear additive sieve for finding prime numbers, Communications of the ACM 24 (1981), 18–23.
- ^ Paul Pritchard, Explaining the wheel sieve, Acta Informatica 17 (1982), 477–485.
- ^ Paul Pritchard, Fast compact prime number sieves (among others), Journal of Algorithms 4 (1983), 332–344.
- ^ Hardy & Wright 1979, thm. 328
Литература
[уреди | уреди извор]Овај одељак би требало проширити. Можете помоћи додавањем садржаја. |
Додатна литература
[уреди | уреди извор]- „Improved Incremental Prime Number Sieves”. Пола Питхарда










![{\displaystyle S_{np_{i+1}}=F_{p_{i+1}}[S_{n}\cup S_{n}+n\cup S_{n}+2n\cup ...\cup S_{n}+n(p_{i+1}-1)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e8ff5329337b78c6f07b0ea24315fc6f92bd3d6)


