Kružno rastavljanje

Kružno rastavljanje sa n=2x3x5=30. Nema prostih brojeva u žutim područjima.

Kružno rastavljanje je metoda za obavljanje preliminarnog smanjenja potencijalnih prostih brojeva od početnog skup svih prirodnih brojeva 2 i većih; verovatno od donošenja liste rezultata potencijalnih prostih brojeva do Eratostenovog sita ili drugih sita koja razdvajaju prostih brojeva iz složenih, ali može i dodatno da se koristi kao prost broj sito utovarivač po sebi od rekurzivne primene kružnog rastavljanja generacije algoritma. Mnogo definitivno rade na kružnom rastavljanju, sita koriste kružno razlaganje, i krug sita, je smislio Pol Prithard iu formulisanju niza različitih algoritama. Da bi se pokazala upotreba kružnog rastavljanja grafički, jedan počinje da piše prirodne brojeve po krugovima kao što je prikazano na dijagramu. Prosti brojevi su u najužem krugu imaju svoje slične pozicije u drugim krugovima, formirajući krakove prostih brojeva. Umnožak prostih brojeva u najužem krugu formi žica složenih brojeva u spoljašnjim krugovima.

Uzorak grafičkog postupka

1. Pronađi prvih nekoliko prostih brojeva tako da formiraju osnove kružnog rastavljanja. Oni su poznati ili možda određeni iz prethodnih aplikacija manjih kružnih rastavljanja ili ih je brzo pronađi koristeći Eratostenovo sito.

1. Množenje baznih osnovnih brojeva zajedno daje rezultat n koji je obim kružnog razlaganje.

1. Napiši brojeve od 1 do n u krug. Ovo će biti najunutrašnjiji krug koji predstavlja jednu kružnu rotaciju.

1. Za brojeve od 1 do n u najužem krugu, udar iskljuje sve umnoške baznih prostih brojeva iz jednog koraka kako se primenjuje u koraku 2. Ova složena eliminacija broja se može postići ili upotrebom sito kao što je Eratostenovo sito ili kao rezultat primene manjih kružnih rastavljanja.

1. Uzimajući da je x broj krugova napisanih do sada, nastavi sa pisanjem xn + 1 to xn + n u koncentričnim krugovima najudaljenijeg kruga, tako da xn + 1 je samo pozicija kao i (x − 1)n + 1.
2. Ponovite korak 5 do najveće rotacije kruga koji obuhvata najveći broj testiranja prostih.
3. Izbrisati broj 1.

1. Izbrisati sve poluge prostih brojeva kao u koraku 1 i primeniti u koraku 2 u svim spoljašnjim krugovima, bez odjave prostih brojeva u najunutrašnjijem krugu (u krugu 1).
2. Izbrisati poluge svih prostih brojeva izbrisanih iz užeg kruga 1 u koraku 4 na isti način kao i brisanje poluge od osnovnih prostih brojeva u koraku 8.
3. Preostali brojevi u krugu su uglavnom prosti brojevi (oni se kolektivno nazivaju "relativno" prosti brojevi). Koristiti druge metode kao što su Eratostenovo sito ili dalju primenu većih kružnih raslojavanja za uklanjanje preostalih ne-prostih brojeva.

Primer

Kružno rastavljanje gde je n=2x3=6

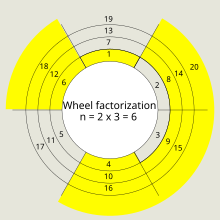
1. Naći prvo 2 prosta broja: 2 i 3.

2. n = 2 × 3 = 6

3.

 1  2  3  4  5  6

4. Isključiti činioce 2 i 3 koji su kao i 4 i 6 činioci 2; 6 kao jedini činilac 3 je već pogođen:

 1  2  3  4  5  6

5. x = 1. xn + 1 = 1 · 6 + 1 = 7. (x + 1)n = (1 + 1) · 6 = 12. Napiši od 7 do 12 sa 7 usklađen sa 1.

 1  2  3  4  5  6
 7  8  9 10 11 12

6. x = 2. xn + 1 = 2 · 6 + 1 = 13. (x + 1)n = (2 + 1) · 6 = 18. Napiši od 13 do 18 Ponovite postupak za nekoliko narednih redova.

 1  2  3  4  5  6
 7  8  9 10 11 12
13 14 15 16 17 18
19 20 21 22 23 24
25 26 27 28 29 30

7 i 8. Prosejavanje

 1  2  3  4  5  6
 7  8  9 10 11 12
13 14 15 16 17 18
19 20 21 22 23 24
25 26 27 28 29 30

9. Prosejavanje

 1  2  3  4  5  6
 7  8  9 10 11 12
13 14 15 16 17 18
19 20 21 22 23 24
25 26 27 28 29 30

10. Dobijena lista sadrži ne-prosti broj 25 koji je 5². Koristi druge metode kao što je sito da bi se eliminisanjem došlo do

2 3 5 7 11 13 17 19 23 29

Paziti da upravo pomoću sledećeg primarnog broj 5 ciklusa krugova i eliminisanjem višestrukog (s) prostog broja (i to samo prostog) sa liste rezultata, dobili smo bazu kruga po koraku 4 za kružno razlaganje sa osnovnim prostim brojevivima od 2, 3 i 5; ovo je jedan krug unapred prethodne 2/3 kružnog rastavljanja. Jednom bi mogli da pratite korake na korak 10 koristeći sledeći uspeh u 7 ciklusu i samo otklanjanje 7 sa liste rezultata u koraku 10 (ostavljajući neke "relativno" proste brojeve u ovom slučaju i sve uzastopne slučajeve - odnosno nije istina potpuno kvalifikovanih prostih brojeva), da bi sledeći dalji napredni krug, rekurzivno ponavljajući korake neophodni su sukcesivno veći krugovi.

Analize i računarska implementacija

Formalno, metoda koristi sledeća saznanja: prvo, da je skup osnovnih prostih ujedinjen sa svojim (beskonačno) nadskup prostih brojeva. Drugo, da beskonačan niz može lako da se odvoji po osnovi između 2 i osnove para proizvoda. (Paziti da 1 zahteva posebno rukovanje.)

Kao što se vidi na primeru, rezultat ponovljenih aplikacija rekurzivnim postupkom iz koraka 4 do 10 može biti lista kruga koji obuhvata bilo koje željeno prosejavanje opsega (na koje se može skratiti) i lista rezultira zatim obuhvata samo umnoške prostih brojeva veći od jedne poslednje polovine osnovnih prostih brojeva.

Paziti da krug prostire željenu gornju granicu prosejavanja opsega, može se zaustaviti stvaranje dodatnih krugova i koristiti informacije iz tog kruga od otpadaka preostalih složenih brojeva sa tog spiska prošlog kruga pomoću Eratostenovog sita tipa tehnike ali koristeći obrazac karakterističan za krug da bi izbegle suvišne kupl; neke optimizacije će moći da se vrše na osnovu činjenice da (biće dokazano u sledećem odeljku) da neće biti ponavljanja kupling bilo kog složenog broja: svaki preostali složeni broj će se poništiti tačno jedanom. Alternativno, može da nastavi da generiše skraćene liste lako pomoću prostih brojeva do kvadratnog korena željenog sita, u tom slučaju će svaki preostali broj reprezentacije u krugu biti glavni; Međutim, iako je ovaj metod efikasan za redukciju složenih brojeva više puta, on gubi mnogo vremena spoljno na kupling operacije u obradi krugova uzastopnih prelaza. Eliminacija složenih brojevakružnog raslojavanja je zasnovan< na sledećem: Za dati broj k > n znamo da K nije prost ako k mod n i n nisu uzajamno prosti. Od toga, deo brojeva koje može sito da eliminiše se utvrdi (mada nisu svi fizički raskinuti, a mnogi se mogu automatski poništiti u radu kopiranja manjih krugova do većim krugova) kao 1 - phi (n) / n, koja je i efikasnost sita

Pošto je poznato

$\lim \inf {\frac {\varphi (n)}{n}}\log \log n=e^{-\gamma }.$

gde je γ Ojlerova konstanta,   γ = 0.577215665...,   e^−γ = 0.56145948... . Ovaj phi(n) / n ide polako do nule kako se n povećava do beskonačnosti i može se videti da ova efikasnost raste veoma sporo do 100% za beskonačno velike n. Od svojstava phi, to se lako može videti da je najefikasnije sito manje od x je ono gde je $n=p_{1}p_{2}...p_{i}<x$ i $n*p_{i+1}>=x$ (tj kružna generacija se može zaustaviti kada poslednji krug prolazi ili ima dovoljan obim da obuhvati najveći broj u opsegu prosejavanja).

Da budu maksimalno korišćenji na računaru, želimo brojeve koji su manji od n i relativno prosti kao skup. Koristeći nekoliko zapažanja, par može lako biti generisan:

1. Početi sa $S_{1}=\{1\}$, čiji par je za $n=1$ sa 2 kao prvi prost broj. Ovaj početni skup znači da su svi broj sa početkom uključeni kao "relativno" prosti brojevi obima kruga 1.
2. Prateći parove koji su $S_{2}=\{1\}$ što znači da počinje sa 3 za sve neparne brojeve sa činiocima 2 otklonjen (obim 2), $S_{6}=\{1,5\}$ je činilac 2. i 3. eliminisani (obim 6) kao polazna osnova za točak u gornjem primeru i tako dalje.
3. Pustiti $S_{n}+k$ da bude skup u kojem je k dodat svakom elementu $S_{n}$.
4. Tada$S_{np_{i+1}}=F_{p_{i+1}}[S_{n}\cup S_{n}+n\cup S_{n}+2n\cup ...\cup S_{n}+n(p_{i+1}-1)]$gde predstavlja operaciju uklanjanja svih množilaca x.
5. 1 i $p_{i+1}$ biće dva najmanja broja skupa $S_{n}$ kada je  $n>2$ otklanja potrebu za računanje prostih brojeva odvojeno iako algoritam ne treba da vodi evidenciju o svim otklonjenim osnovnim prostim brojevima koji više nisu uključeni u narednim parovi.
6. Svi parovi gde je obim n > 2su simetrične oko $n/2$, smanjivanjem uslova skladištenja. Sledeći algoritam ne koristi ovu činjenicu, ali je zasnovan na činjenici da su razlike između uzastopnih brojeva u svakom paru simetrične oko pola puta tačke.

Vidi još

• Sundaramovo sito
• Teorija sita

Dodatna literatura

• „Improved Incremental Prime Number Sieves”.  Pola Pitharda

Spoljašnje veze

• Wheel Factorization