Grejev kod

Reflektovani binarni kod, takođe poznat kao Grejev kod po Frenku Greju, je sistem binarnih cifara u kojem se dve uzastopne vrednosti razlikuju u samo jednom bitu (Binarne cifre ). Reflektovani binarni kod je prvobitno projektovan da spreči lažni izlaz iz elektromehaničkih prekidača. Danas, Grejevi kodovi se široko koriste da olakšaju ispravljanje grešaka u digitalnim komunikacijama, kao što su digitalne zemaljske televizije i neki kablovski sistemi.

Ime[uredi | uredi izvor]

Frenk Grej, naučnik iz Belovih laboratorija, uveo je termin reflektovani binarni kod u njegovoj opštepoznatoj aplikaciji iz 1947. godine, tvrdeći da je kod imao "još nema ime"^[1] On je izveo ime iz činjenice da je "moguće izgraditi od konvencionalnih binarnih kodova kao vrsta refleksije procesa".

Kod je kasnije nazvan po Greju od strane drugih koji su ga koristili. Dve različite 1953 patent aplikacije koriste Grejev kod kao alternativno ime za "reflektovani binarni kod";^[2]^[3] jedan od ovih takođe navodi "minimalna greška koda" i "ciklična permutacija koda" među imenima .^[3] 1954 patent aplikacija se odnosi na " zvono telefona Grejevog koda ".^[4]

Motivacija[uredi | uredi izvor]

Mnogi uređaji ukazuju na poziciju otvaranja i zatvaranja prekidača. Ako taj uređaj koristi prirodne binarne kodove, pozicije 3 i 4 su jedna do druge ali sva tri bita binarne predstave se razlikuju:

Decimalni	Binarni
...	...
3	011
4	100
...	...

Problem sa prirodnim binarnim kodovima je da će, sa fizičkim, mehaničkim prekidačima, vrlo retko da promene stanje tačno sinhronizovano. Na prelazu između dva stanja, prikazanim iznad, sva tri prekidača menjaju stanje. U kratkom periodu dok se svi menjaju, prekidači će pročitati neku lažnu poziciju. Čak i bez prekidača, tranzicija može da izgleda 011 — 001 — 101 — 100. Kada su prekidači u poziciji 001, posmatrač ne može reći da li je stvarna pozicija 001, ili je tranziciono stanje između druge dve pozicije. Ako se izvršen rad napaja unutar sekvencijalnog sistema, verovatno preko kombinacione logike, onda će sekvencijalni sistem da skladišti lažnu vrednost.

Reflektovani binarni kod rešava ovaj problem tako što će promeniti samo jedan prekidač u jednom trenutku, tako da nikada ne postoji dvosmislenost pozicije,

Decimalni	Binarni	Grej	Grej kao Decimalni
0	000	000	0
1	001	001	1
2	010	011	3
3	011	010	2
4	100	110	6
5	101	111	7
6	110	101	5
7	111	100	4

Primećuje se da stanje 7 može da pređe u stanje 0 sa samo jednom promenom prekidača. To se naziva "ciklično" vlasništvo Grejevog koda. U standardnom Grejevom kodiranju najmanji značajni bit prati šablon koji se ponavlja isključeno 2 uključeno, 2 isključeno (...11001100...); sledeća cifra obrazac isključeno 4 uključeno, 4 isključeno i tako dalje.

Više formalno, Grejev kod je kod prepisan svakome od skupa celih brojeva, ili svakom članu cirkularne liste, reč simbola kao što svaka dva susedna koda reči pripadaju jednom simbolu. Ovi kodovi su takođe poznati kao jedno-razdeljinski kodovi, reflektujući Hamingovo rastojanje od 1 između susednih kodova. Tamo može biti više od jednog Grejevog koda za datu dužinu reči, ali termin je prvo upotrebljen na određeni binarni kod za ne-negativne cele brojeve, Binarno reflektujući Grejev kod, ili BRGK, trobitna verzija koja je prikazana iznad.

Istorija i praktična aplikacija[uredi | uredi izvor]

Reflektivni binarni kod je bio primenjen na matematičku slagalicu pre nego što je postao poznat inženjerima. Francuski inženjer Emil Baudot je koristio Grejev kod u telegrafiji 1878.^[5] On je primio francuski orden Legiju časti za svoj rad. Grejev kod se ponekad prepisuje nepravilno,,^[6]za Elišu Grej ( na principima modulacije impulsnog koda, K. V. Katermol,^[7] na primer).

Frank Grej, koji je postao poznat za stvaranje signalnog metoda koji se koristi za kompatibilni televizor u boji, izmislio je metod da pretvori analogne signale u reflektivne grupe binarnih kodova koristeći aparat zasnovan na elektronskim cevima. Metoda i aparati su bili patentirani 1953 i ime Grej je ostalo u kodovima. "Impulsna kodna modulaciona cev", naprava koju je Grej patentirao je napravljena od strane Rejmonda B. Searsa od Bela Labsa, radeći sa Grejem i Vilijamom M. Gudolom, koji je dao zasluge Greju za ideju reflektivnog binarnog koda. ^[8]

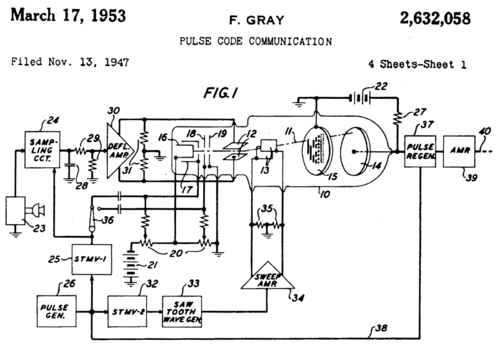
Upotreba njegovih istoimenih kodova za koje je Grej najviše bio zainteresovan bila je da smanji efekat greške u razgovoru analognih signala do digitalizacije; njegovi kodovi se još uvek koriste danas za ovu svrhu i druge.

Pozicioni koderi[uredi | uredi izvor]

Grejev kod se koristi u poziciji kodera (Linearnog kodera i rotacionog kodera), u želji da se jednostavno binarno kodira. Ovim se izbegava mogućnost da, kada se nekoliko bitova menja u binarnoj reprezentaciji pod uglom, a procena će rezultirati od nekog od bitova promene pre drugih. Prvobitno, obrazac je bio električno provodljiv, podržan (u rotacionom koderu) izolacionim diskom. Svaka staza je imala svoj stacionarni metalni kontakt sa oprugom; još jedan kontakt koji je napravio vezu sa uzrokom. Taj zajednički kontakt je povezan uzrokom na bilo koji od kontakata staze na odmoru provodnog obrasca. Međutim, klizni kontakti se pohabaju i potrebno im je održavanje, koje favorizuje optičke kodere.

Bez obzira na usklađivanju kontakata, i tačnost uzroka, prirodni-binarni kod će imati greške na određenim pozicijama diska, jer je nemoguće da se svi bitovi promene u isto vreme dok se disk okreće. Isto važi i za optičke kodere; Prelazi između netransparentnih i transparentnih se ne mogu istovremeno odvijati za određene tačne pozicije. Rotacioni koderi koriste cikličnu prirodu Grejevog koda, jer uzastopni položaji sekvence se razlikuju za samo jedan bit. To znači da, za tranziciju iz stanja A u stanje B, vremenski nesklad može samo da utiče kada se A → B tranzicija javlja, pre nego ubacivanjem jednog ili više (do n - 1 za N-bitnu kodnu reč) lažnu među stanjima, kako bi došla ako se koristi standardni binarni kod.

Hanojska kula[uredi | uredi izvor]

Binarni ogledi Grejevog koda mogu se koristiti kao vodič rešenja za problem Hanojske kule, kao i klasične kineske slagalice prstenova, sekvencijalne mehaničke slagalice mehanizma.^[6]Takođe formira Hamiltonov ciklus na hiperkubu, gde se svaki bit vidi kao jedna dimenzija.

Genetski algoritmi[uredi | uredi izvor]

Zbog svojstva Hamingove udaljenosti od Grejevog koda, oni se ponekad koriste u genetskim algoritmima. Oni su veoma korisni u ovoj oblasti, jer mutacije u kodu omogućavaju uglavnom postepene promene, ali povremeno promena jednog bita može izazvati veliki skok i dovesti do novih svojstava.

Karnoova karta[uredi | uredi izvor]

Grejevi kodovi se takođe koriste u označavanju osa Karnoove karte.^[9]

Ispravka greške[uredi | uredi izvor]

U modernoj digitalnoj komunikaciji, Grejevi kodovi igraju važnu ulogu u ispravljanju greške. Na primer, u digitalnim modulacionim šemama kao što je KAM gde se podaci obično prenosi u simbolima od 4 bita ili više, signali konstelaciskog dijagrama su uređeni tako da se obrasci bitova prenose od sazvežđa susednih tačaka razlikujući se samo za jedan bit. Kombinovanjem sa ranom korekcijom grešaka sposobnom da ispravlja jednobitne greške, moguće je da prijemnik ispravi sve greške prenosa koje uzrokuju da sazvežđa ukazuju na odstupanja u oblasti susedne tačke. To čini prenosni sistem manje podložan bukom

Komunikacija između domena sata[uredi | uredi izvor]

Digitalni Logički dizajneri koriste Grejev kod intenzivno za donošenje multi-bitnih broja informacija između sinhroni logike koja posluje na različitim časovnim frekvencijama. Logika se smatra da posluje u različitim "domenima sata". To je osnova za projektovanje velikih čipova koji rade sa mnogo različitih frekvencija časovnika.

Brojači Grejevog koda i aritmetika[uredi | uredi izvor]

Tipična upotreba brojača Grejevog koda gradi PUPV (prvi-u, prvi-van) međumemoriju podatka, koji čitaju i pišu portove koji postoje u različitim domenima sata. Ulazni i izlazni brojači unutar tih dualnih portova PUPV su često čuvani koristeći Grejev kod za sprečavanje nevažećih prelaznih stanja od zarobljavanja, kada datoteka prelazi domen sata.^[10] Ažurirani čitani i pisani pokazivači treba da budu usvojeni od domena sata kada se menjaju, da bi mogli da prate PUPV prazan i punopravni status u svakoj oblasti. Svaki bit od pokazivača je odabran ne-deterministički za taj transfer domena sata. Dakle, za svaki bit, bilo stara vrednost ili nova vrednost se propagira. Dakle, ako više od jednog bit u multi-bitni pokazivač se menja u trenutku uzorkovanja, kao "pogrešna" binarna vrednost (ni nova ni stara) može biti propagirana. Garantujući samo jedan bit može da se menja, Grejev kod garantuje da jedine moguće odobrene vrednosti su nove ili stare više-bitne vrednosti. Tipični Grejevi startne dve dužine se koriste.

Ponekad digitalni autobusi u elektronskim sistemima se koriste za prenos količina koje se samo mogu povećati ili smanjiti jedan po jedan, na primer, izlaz za događaj koji se dogodio između domena sata ili na digitalno-analognom konvertoru. Prednost Grejevog koda u ovim aplikacijama je da razlike u propagiranju odlaganja mnogih provodnika koji predstavljaju delove koda ne mogu izazvati primljene vrednosti prolazeći kroz stanja koja su van Grejevih sekvenci. Ovo je slično ka prednostima Grejevog koda u izgradnji mehaničkih kodera, međutim, izvor Grejevog koda je elektronski brojač u ovom slučaju. Sam brojač mora računati u Grejevom kod, ili ako je u suprotnosti u binarnom onda izlazna vrednost od brojača mora biti izmerena nakon što je pretvorena u Grejev koda, jer kada je vrednost pretvorena iz binarnog u Grejev kod, moguće je da će razlike u vremenu dolaska binarnih bitova podataka u binarnu Grejevu konverziju kola značiti da je broj mogao ukratko proći kroz stanja koja su divlja u redosledu. Dodavanje registara sata posle sklopa koji pretvara broj vrednost Grejevog koda može uvesti sat ciklusa kašnjenja, pa računanje direktno u Grejevom kodu može biti korisno. Brojač Grejevog koda je patentiran 1962 US3020481 i bilo je mnogo drugih od tad. U novije vreme brojač sivog koda može biti implementiran kao stanje mašine u Verliogu. Da bi se sproveo sledeći broj vrednosti neophodno je da se koristi kombinovana logika koja će prirasti trenutnu brojevnu vrednost koja se skladišti u Grejevom kodu. Verovatno najočigledniji način da povećate cifru Grejevog koda je da ga pretvoriti u običan binarni kod, dodajte jedan tome sa standardnim binarnim dodatkom, a zatim pretvorite rezultat nazad u Grejev kod. O ovom pristupu je razgovarano u novinama 1996. godine^[11], a potom je i patentirano od strane nekog drugog 1998 US5754614 . Druge metode brojanje u Grejevom kodu se raspravljaju u izveštaju R. V. Dorana, uključujući i uzimanje izlaza iz prvih reza flip flopsa u binarnom brojaču talasanja .^[12]

Možda je najčešći elektronski brojač sa "samo jednim promena bita u vremenu " imovina je Džonsonov brojač .

Konstrukcija n-bitnog Grejevog koda[uredi | uredi izvor]

Binarne refleksije Grejevog koda lista za n bitova može biti rekurzivno generisana iz liste za n-1 bitova po reflektovanju liste ( tj listanje stavki obrnutim redosledom ), nadovezivanjem originalnih listi sa obrnute liste, prefiksi unosa u originalni spisak sa binarnom cifrom 0, a zatim fiksiranje stavke u reflektujuću listu sa binarnom cifrom1. Na primer, generisanjem n=3 liste od n=2 liste :

2-bitna lista:	00, 01, 11, 10
Reflektovani:	10, 11, 01, 00
Prefiks starog unosa sa 0:	000, 001, 011, 010,
Prefiks novog unosa sa 1:	110, 111, 101, 100
Spojeni:	000, 001, 011, 010,	110, 111, 101, 100

Jedan bit Grejevog koda je G₁ = ( 0, 1 ) . Ovo se može posmatrati kao izgrađeno rekurzivno kao što gore nula-bitni Grejev kod G₀ = {Λ} se sastoji od jednog ulaska nulte dužine. Ovaj učestali proces stvaranja G_n+1 od G_n daje sledeće osobine standardnog reflektujućeg koda jasnim:

G_n je permutacija brojeva 0, .., 2ⁿ-1 . ( Svaki broj se pojavljuje tačno jednom u listi. )
G_n je ugrađen kao prva polovina od G_n+1
Stoga kodiranje je stablo, u smislu da se jednom binarni broj pojavljuje u G_n, pojavljuje se u istom položaju u svim dužim listama; tako da ima smisla govoriti o refleksivnoj vrednosti broja Grejevog koda G(m) = m- ti reflektujući Grejev kod, računajući od 0 .
Svaki unos u G_n razlikuje se samo po jednom bitu od prethodnog unosa. (Hamingova udaljenost je 1)
Poslednji unos u G_n razlikuje se samo po jednom bitu od prvog unosa (Kod je cikličan)

Ove karakteristike ukazuju na jednostavan i brz način prevođenja binarnih vrednosti u odgovarajući Grejev kod. Svaki bit je rotiran ako je sledeći veći bit ulazne vrednosti postavljen na jedan. Ovo se može izvršiti paralelno od bitne-smene i isključivo - ili rukovanjem ako su dostupni : n-ti grejev kod se dobija izračunavanjem $n\oplus \lfloor n/2\rfloor$

Sličan postupak se može koristiti za izvođenje suprotnih prevoda, ali računanje svakog bita zavisi od izračunate vrednost sledećeg višeg bita tako da se ne može vršiti paralelno. Pod pretpostavkom da je g_i bit i-tog Grejevog koda (g₀ je najviše značajan bit), i b_i je bit i-tog binarnog koda (b₀ je najviše značajan bit) obrnut prevod može dati rekurzivno: b₀=g₀ i b_i=g_i $b_{i}=g_{i}\oplus b_{i-1}$ . Alternativno, dekodiranje Grejevog moda u binarni broj se može opisati kao prefiks zbira bitova u Grejevom kodu, gde svaki pojedinac operacije u prefiksu sume se vrši po modulu dva.

Da iterativno izgradite binarno-reflektujući Grejev kod, korak 0 počnite sa kod₀ = 0, a na korak i>0 nađi poziciju buta najmanje težine 1 u binarnoj zastupljenosti od i pomerite bit na prethodni položaj koda_i-1 da biste dobili sledeći kod kod_i . Pozicije bitova počinje sa 0, 1, 0, 2, 0, 1, 0, 3, ... ( sekvenca A007814 u OEIS) . Pogledajte pronađi prvi set za efikasne algoritme za izračunavanje ove vrednosti .

Pretvaranje do i od Grejevog koda[uredi | uredi izvor]

Sledeće funkcije u C pretvaraju između binarnih brojeva i njihovih povezanih Grejevih kodova. Iako može izgledati da Grej-na-binarni konverzija zahteva da se sa svakim bitom rukuje jedan po jedan, brže algoritmi postoji . ^[13]

/*
 * Ова функција конвертује непотписани бинарни
 * број рефлектује бинарни Грејев код.
 *
 * Оператор >>је смена десно. Оператор ^ је искључив или.
 */
unsigned int binaryToGray(unsigned int num)
{
    return num ^ (num >> 1);
}

/*
 * Ова функција конвертује непотписани бинарни
 * број рефлектује бинарни Грејев код.
 * Сваки бит Грејевог кода искључиво изводе набројане са свим
 * више значајних битова.
 */
unsigned int grayToBinary(unsigned int num)
{
    unsigned int mask;
    for (mask = num >> 1; mask != 0; mask = mask >> 1)
    {
        num = num ^ mask;
    }
    return num;
}

/*
 * Ефикаснији верзија за Грејеве кодове од 32 или мање бита.
 */
unsigned int grayToBinary32(unsigned int num)
{
    num = num ^ (num >> 16);
    num = num ^ (num >> 8);
    num = num ^ (num >> 4);
    num = num ^ (num >> 2);
    num = num ^ (num >> 1);
    return num;
}

Specijalni tipovi Grejevih kodova[uredi | uredi izvor]

U praksi, "Grejev kod" gotovo uvek se odnosi na binarni - reflektujući Grejev kod ( BRGK ) . Međutim, matematičari su otkrili i druge vrste Grejevog koda. Kao BRGK, svaki se sastoji od liste reči, gde svaka reč se razlikuje od sledeće u samo jednoj cifri ( svaka reč ima Hamingovu udaljenost 1 od sledeće reči ) .

n-arni Grejev kod[uredi | uredi izvor]

Trostruki broj→ trostrukog Grejevog koda

Postoje mnoge specijalizovane vrste Grejevih kodova osim u binarnom-reflektujućem Grejevom kodu . Jedan takav tip Grejevog koda je n-arni Grejev kod, takođe poznat kao ne- logički Grejev kod . Kao što samo ime kaže, ovaj tip Grejevog koda koristi ne - logičku vrednost u svojim kodiranjima.

Na primer, trostruki Grejev kod će koristiti vrednosti {0, 1, 2 } . ( n, k ) -Grejev kod je n-arni Grejev kod sa k ciframa^[14]. Sekvenca elemenata u ( 3, 2 ) -Grejevom kodu je : { 00, 01, 02, 12, 10, 11, 21, 22, 20 } . ( n, k ) -Grejev kod može biti konstruisan rekurzivno, kao BRGK, ili može biti konstruisan iterativno . Algoritam za iterativno generisanje ( n, k) -Grejevog koda je predstavljen ( u C) :

// улази: база, бројеви, вредности
// излаз: греј
// Претварање вредности на грејевим кодовима са датом базом и цифром.
// Итеративно путем низа вредности ће резултирати у низу
// грејев код у којем само једна цифра се мења у времену.
void to_gray(unsigned base, unsigned digits, unsigned value, unsigned gray[digits])
{
	unsigned baseN[digits];	//Залихе обичних база Н бројева, једна цифра по уносу
	unsigned i;		// Променљива петља
 
	// Ставите нормалну базуН броја у базу низа. На базу 10, 109
	// биће складиштено као [9,0,1]
	for (i = 0; i < digits; i++) {
		baseN[i] = value % base;
		value = value / base;
	}
 
	// Претвори нормалан базуН броја у еквивалентан грејев код. Напоменути да
	// петља почиње у најзначајније цифре и пада.
	unsigned shift = 0;
	while (i--) {
		// Цифре греја су померене доле сумом већих
		// бројеви.
		gray[i] = (baseN[i] + shift) % base;
		shift = shift + base - gray[i];	// Претварање вредност на грејев код са датом базом и цифрама. Одузимање од базе, такав помак је позитиван
	}
}
// примери
// улаз: вредности = 1899, base = 10, digits = 4
// излаз: базаН[] = [9,9,8,1], gray[] = [0,1,7,1]
// улаз: вредност = 1900, base = 10, digits = 4
// излаз: базаН[] = [0,0,9,1], gray[] = [0,1,8,1]

Postoje i drugi algoritmi Grejevog koda za ( n, k) -Grejev kod .( n, k ) -Grejev kod proizveden od strane algoritma iznad uvek je cikličan; neki algoritmi, kao što su Guan,^[14] nemaju ovu osobinu kada je k neparno. S druge strane, dok samo jednu cifru istovremeno menjamo sa ovim metodom, ona može promeniti obavijanjem ( petlja je od n-1 do 0 ) . U Guan algoritma, račun naizmenično raste i pada, tako da je numerička razlika između dve cifre grejevog koda uvek jedan .

Grej kodovi nisu jedinstveno definisani, jer je permutacija kolona takvog koda kao sivi kod. Navedeni postupak proizvodi kod u kome je manji značaj cifre, češće se menja, što je slično sa uobičajenim postupcima prebrojavanja .

Pogledajte takođe poprečni binarni sistem brojeva, varijanta trostrukog brojevnog sistema u kojem najviše 2 cifre menjaju svoj prirast, jer svaki porast može da se uradi sa najviše jednom cifrom nošenja operacije .

Balansirani Grejev kod[uredi | uredi izvor]

Iako je binarni reflektujući Grejev kod koristan u mnogim scenarijima, nije optimalan u nekim slučajevima zbog nedostatka " uniformnosti ".^[15] U izbalansiranim Grejevim kodovima, broj promena u različitim pozicijama koordinate je što je bliže moguće. Da bi to precizirali, neka bude G R-arni kompletan ciklus Greja imajući tranziciju sekvence b_k; u tranziciji tačaka (Spektra) od G su prikupljani celi brojevi koji su definisani

\lambda _{k}=|\{j\in \mathbb {Z} _{R^{n}}:\delta _{j}=k\}|\,,{\text{ for }}k\in \mathbb {Z} _{R}

Grejev kod je jednak ili jednako izbalansiran ako njegove tranzicione tačke su sve jednake, u tom slučaju imamo $\lambda _{k}=R^{n}/n$ za sve k. Jasno, kada je $R=2$ , takvi kodeksi postoje samo ako je n jačine 2. U suprotnom, ako je n ne deli $R^{n}$ ravnomerno, moguće je izgraditi dobro uravnotežene kodove gde je svaka tranzicija datoteke ili $\lfloor R^{n}/n\rfloor$ ili $\lceil R^{n}/n\rceil$ . Grejevi kodovi mogu takođe biti eksponencijalno uravnoteženi ako sve njihove tranzicije tačaka su susedne jačine dva, i takvi kodeksi postoje za svaku jačinu dva . ^[16]

Na primer, uravnotežen 4 -bitni Grejev kod ima 16 prelaza, koji se mogu ravnomerno rasporediti u sve četiri pozicije (četiri prelaza na poziciji ), što ga čini ravnomerno izbalansiranim :

0 1 1 1 1 1 1 0 0 0 0 0 0 1 1 0 
0 0 1 1 1 1 0 0 1 1 1 1 0 0 0 0 
0 0 0 0 1 1 1 1 1 0 0 1 1 1 0 0 
0 0 0 1 1 0 0 0 0 0 1 1 1 1 1 1

dok uravnoteženi 5 - bitni Grejev koda ima ukupno 32 prelaza, koji se ne mogu ravnomerno rasporediti među pozicijama. U ovom primeru, četiri pozicije imaju po šest prelaza, i jedna ima osam : ^[15]

1 1 1 1 1 0 0 0 0 1 1 1 1 1 1 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 
0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 1 1 0 0 0 
1 1 0 0 1 1 1 0 0 0 0 0 0 1 1 1 0 0 0 1 1 1 1 1 1 0 0 0 0 0 1 1 
1 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 1 
1 1 1 1 1 1 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 1 0 0 0 1 1 1 1 1 1

Mi ćemo sada pokazati konstrukciju za dobro izbalansiran binarni Grejev kod koji nam omogućava da generišemo N cifre izbalansiranog Grejevog koda za svako n ^[17] Osnovni princim je da se induktivno kostruiše (n+2) broj Grejevog koda G' - daje n-cifreni Grejev kod G na takav način da je izbalansirana imovina sačuvana. Da bi ovo uradili, mi smatramo particije na G=g₀,......g_2ⁿ-1 u paran broj L, ne praznih blokova u obliku

\{g_{0}\},\{g_{1},\ldots ,g_{k_{2}}\},\{g_{k_{2}+1},\ldots ,g_{k_{3}}\},\ldots ,\{g_{k_{L-2}+1},\ldots ,g_{-2}\},\{g_{-1}\}

gde $k_{1}=0,k_{L-1}=-2$ , i $k_{L}=-1$ (mod $2^{n}$ ). Ova podela indukuje $(n+2)$ -cifre Grejevog koda date od

00g_{0},

00g_{1},\ldots ,00g_{k_{2}},01g_{k_{2}},\ldots ,01g_{1},11g_{1},\ldots ,11g_{k_{2}},

11g_{k_{2}+1},\ldots ,11g_{k_{3}},01g_{k_{3}},\ldots ,01g_{k_{2}+1},00g_{k_{2}+1},\ldots ,00g_{k_{3}},\ldots ,

00g_{-2},00g_{-1},10g_{-1},10g_{-2},\ldots ,10g_{0},11g_{0},11g_{-1},01g_{-1},01g_{0}

Ako definišemo umnoženu tranziciju $m_{i}=|\{j:\delta _{k_{j}}=i,1\leq j\leq L\}|$ da je broj puta u kojoj se cifra u poziciji i menja između uzastopnih blokova u particiji, zatim za ( n + 2 ) -broj Grejevog koda izazvana od ove podele tranzicije spektra $\lambda '_{k}$ je

\lambda '_{k}={\begin{cases}4\lambda _{k}-2m_{k},&{\text{if }}0\leq k<n\\L,&{\text{ otherwise }}\end{cases}}

Delikatan deo ove konstrukcije je da pronađe adekvatnu podelu uravnoteženog Grejevog koda N-cifri koji suizazvali kod da ostane izbalansiran. Ujednačeni kodovi se mogu naći kada je $R\equiv 0\mod 4$ i $R^{n}\equiv 0\mod n$ , a ova konstrukcija može biti produžena do R -arnog slučaja.^[17]

Monotoni Grejev kod[uredi | uredi izvor]

Monotoni kodovi su korisni u teoriji interkonekcije mreža, posebno za minimiziranje dilatacije za linearne nizova procesora.^[18] Ako definišemo težinu binarnog niza da je broj 1s u nizu, onda iako mi jasno ne može imati Grejev kod sa strogo povećanom težinom, možemo želeti da približimo to tako što kod podelimo u dve susedne težine pre nego što stignu sledeći .

Možemo da formalizujemo koncept monotonog Grejevog koda na sledeći način: razmotriti podelu hiperkuba Q_n = ( V_n, E_n ) u nivoe temena koji imaju jednaku težinu, odnosno

V_{n}(i)=\{v\in V_{n}:v{\text{ has weight }}i\}

za $0\leq i\leq n$ . Ovi nizovi zadovoljavaju $|V_{n}(i)|={\binom {n}{i}}$ . Neka $Q_{n}(i)$ bude podgrafikon od $Q_{n}$ izazvan od $V_{n}(i)\cup V_{n}(i+1)$ , i neka $E_{n}(i)$ bude ivica u $Q_{n}(i)$ . Monotoni Grejev kod je onda Hamiltonov put u $Q_{n}$ tako da kad god $\delta _{1}\in E_{n}(i)$ dođe pre $\delta _{2}\in E_{n}(j)$ u stazi, onda je $i\leq j$ .

Elegantna izgradnja monotonog Grejevog koda sa N-ciframa za svako n zasniva se na ideji rekurzivnim građenje pod staze $P_{n,j}$ dužine $2{\binom {n}{j}}$ imaju ivice u $E_{n}(j)$ .^[18]Mi definišemo $P_{1,0}=(0,1)$ , $P_{n,j}=\emptyset$ kad god $j<0$ ili $j\geq n$ , i

P_{n+1,j}=1P_{n,j-1}^{\pi _{n}},0P_{n,j}

drugačije. Ovde, Pi je prikladno definisana permutacija $P^{\pi }$ odnosi se na putanji P sa svojim koordinatama permutovanim od pi. Ovi putevi dovode do dva monotona Grejeva koda N-cifara $G_{n}^{(1)}$ i $G_{n}^{(2)}$ data od

G_{n}^{(1)}=P_{n,0}P_{n,1}^{R}P_{n,2}P_{n,3}^{R}\cdots {\text{ and }}G_{n}^{(2)}=P_{n,0}^{R}P_{n,1}P_{n,2}^{R}P_{n,3}\cdots

Izbor pi_n koji obezbeđuje da ovi kodovi budu zaista Grejevi kodovi ispostavlja se da je $\pi _{n}=E^{-1}(\pi _{n-1}^{2})$ . Prvih nekoliko vrednosti $P_{n,j}$ su prikazani u tabeli ispod.

Ovi Monotoni Grejevi kodovi mogu biti efikasno sprovedeni na takav način da svaki naredni elemenat se generiše u O(n) vremenu. Algoritam je najlakše opisati korišćenjem korutine.

Monotoni kodovi imaju jednu zanimljivu vezu sa Lovasovom pretpostavkom, u kojem se navodi da svaki povezan najviši - prelazan graf sadrži Hamiltonov put. "Srednji nivo " podgraf K_ { 2n + 1 } ( n) najviši - prelazan (to jest, njegova automorfna grupa je prelazana, tako da svaki čvor ima isto " lokalno okruženje " " i ne može se razlikovati od drugih, jer možemo ponovo označiti koordinate kao binarne cifre da dobijemo automorfizam) i problem nalaženja Hamiltonovog puta u ovom podgrafu se naziva " srednji nivo problema ", koja može da pruži uvid u više opštoj pretpostavci. Na pitanje je potvrdno odgovoreno za n<15, a prethodna konstrukcija za monotone kodove osigurava Hamiltonov put dužine najmanje 0.839N gde je N broj čvorova u sredini nivoa podgrafa.^[19]

Beket-Grejev kod[uredi | uredi izvor]

Druga vrsta Grejevog koda, Beket - Grejev kod, nazvan je za irskog dramskog pisca Semjuel Beket-a, koji je bio zainteresovan za simetriju. Njegova predstava " Dual " ima četiri glumca i podeljen je na šesnaest vremenskih perioda. Svaki period se završava sa jednim od četiri glumaca koji ulazi na ili izlazi sa bine. Predstava počinje sa praznom binom, a Beket žele da se svaki podskup aktera pojavi na bini tačno jedanput.^[20] Jasan skup glumaca trenutno na sceni može se predstaviti sa 4- bitnim binarnim Grejevim kodom. Beket, međutim, stavlja dodatna ograničenje na scenariju : želi da glumci ulaze i izlaze tako da glumac koji je bio na sceni najduže bude taj koji sledeći izlazi. Glumci bi tada mogli biti predstavljen i tako da su prvi u, prvi iz reda, tako da ( od aktera na bini ) glumac koji nema red uvek bude onaj koji je prvi put dobio red.^[20] Beket je bio u stanju da pronađe Beket - Grejev kod za njegovu igru, i zaista, iscrpan popis svih mogućih sekvenci otkriva da takav broj ne postoji za n = 4. Poznato je danas da takvi kodeksi postoje za n = 2, 5, 6, 7, 8 i, i ne postoje za n = 3 ili 4. Primer 8 - bitni Beket - Grejev kod se može naći u Knuthe umetnosti kompjuterskog programiranja^[6] Prema Savadi i Vongu, za pretraživanje prostor za n = 6 mogu biti istraženi u 15 sati, a više od 9.500 rešenja za slučaj N = 7 su pronađeni.^[21]

Zmija u kutiji kod[uredi | uredi izvor]

Zmija u kutiji kodovi, ili zmija, su sekvence čvorova pobuđenih puteva u N - dimenzionalnom grafikonu hiperkuba, i kalem - in-the- bok kodovi, ili kalemovi, su sekvence čvorova namernih ciklusa u Hipercube. Gledano u Grejevom kodu, ove sekvence imaju osobinu da budu u stanju da otkriju bilo koji jedan -bit kodiranja greške. Kodove ovog tipa je prvi opisao V. H. Kautz u kasnim 1950-im;^[22] Od tada, bilo je mnogo istraživanja na pronalaženju koda sa najvećim mogućim brojem šifri za datu dimenziju hiperkuba.

Jedna traka Grejevog koda [uredi | uredi izvor]

Još jedna vrsta Grejevog koda je pojedinačna traka Grejevog koda (STGC) otkrivena od strane Spedinga^[23] i rafinirani od strane Hiltgena, Patersona i Brandestinija u " Pojedinačnoj traci Grejevog koda "(1996).^[24]^[25] STGC je ciklična lista P-a, jedinstvenih binarnih kodiranja dužine n da takve dve uzastopne reči se razlikuju u tačno jednoj poziciji i kada je lista ispitivana kao P×N matrica, svaka kolona je ciklično pomerena prvoj koloni.^[26]

Naziv potiče od njihove upotrebe sa rotacionim koderima, gde je veliki broj numera bio shvaćen kontaktima, što je rezultiralo za svaki izlazu 0 ili 1. Da biste smanjili buku zbog različitih kontakata ne prebacujući u istom momentu, jedna poželjno postavlja tragove tako da izlazni podaci od kontakata su Grejevi kodovi. Da biste dobili visoke ugaone tačnosti, potrebno je dosta kontakata ; u cilju postizanja najmanje 1 preciznosti stupnjeva, potrebno najmanje 360 različitih stavova po revoluciji, što zahteva minimum 9 bitova podataka, a time i isti broj kontakata .

Ako su svi kontakti postavljeni na istim ugaonim pozicijama, 9 staza je potrebno da se dobije standardni BRGK sa najmanje 1 tačnošću stepena. Međutim, ako proizvođač pomera kontakt na druge ugaone pozicije ( ali u istoj udaljenosti od centra osovine ), a zatim odgovarajuće " zvono " treba da se rotira istim uglom da bi dali isti izlaz. Ako najznačajniji bit ( unutrašnji prsten na slici 1 ) dovoljno rotira, tačno odgovara sledećem prstenu napolju. Pošto oba prstena su tada identična, unutrašnji prsten može se isključiti, a senzor za taj prsten preseli u preostali, identičan prsten ( ali ogranak pod tim uglom od drugog senzora na taj prsten ) . Ta dva senzora na jednom prstenu prave kvadratne kodere. To smanjuje broj numera za " 1 stepen rezolucije " ugaonog kodera do 8 numera. Smanjenje broja numera dodatno ne može biti učinjeno sa BRGK .

Dugi niz godina, Torsten Silke^[27] i drugi matematičari su verovali da je bilo nemoguće da kodiraju položaj na jednoj stazi tako da uzastopne pozicije se razlikuju od samo jednog senzora, osim za 2 - senzor, 1 - traka kvadratnog kodera. Dakle, za aplikacije gde bi 8 traka bilo previše glomazno, ljudi su koristili pojedinačnu-traku inkrementalnih enkoder ( kuadraturni koderi ) ili 2 - staza " kvadratnih kodera + referentni nivo" kodera

Napomena Speding je, međutim, registrovao patent 1994. godine sa nekoliko primera koji pokazuju da je moguće .^[23] Iako nije moguće razlikovati 2n pozicije sa n senzorima na jednoj stazi, moguće je razlikovati blizinu mnogih od njih. Na primer, kada je n samo jačine 2, N senzori mogu razlikovati 2n - 2n pozicije .^[28] Hilten i Paterson su objavilo rad 2001. godine izlažući Pojedinačnu-traku Grejevog koda sa tačno 360 ugaonih pozicija, izgrađenih koristeći 9 senzora.^[25] Pošto je taj broj veći od 2⁸ = 256, više od 8 senzori su potrebni za bilo koji kod, iako BRGK je mogao da razlikuje 512 pozicija sa 9 senzora. STGK za p = 30 i n = 5 se ovde reprodukuje :

Jedna traka Grejevog koda za 30 pozicija
Ugao	Kod	Ugao	Kod	Ugao	Kod	Ugao	Kod	Ugao	Kod
0°	10000	72°	01000	144°	00100	216°	00010	288°	00001
12°	10100	84°	01010	156°	00101	228°	10010	300°	01001
24°	11100	96°	01110	168°	00111	240°	10011	312°	11001
36°	11110	108°	01111	180°	10111	252°	11011	324°	11101
48°	11010	120°	01101	192°	10110	264°	01011	336°	10101
60°	11000	132°	01100	204°	00110	276°	00011	348°	10001

Svaka kolona je ciklično pomeranje prve kolone, i iz bilo kog reda u sledeći red samo je jedan bit promene.^[29] Pojedinačna-staza prirode ( poput koda lanac) je korisna u izradi ovih točkova (u poređenju sa BRGK ), kao što je potrebna samo jedna staza, čime se smanjuje njihova cena i veličina. Grejev kod prirode je koristan ( u poređenju sa lancem kodova, koji se nazivaju de Bruijne sekvence), samo jedan senzor će promeniti u bilo kom trenutku, tako da neizvesnosti u toku tranzicije između dva diskretna stanja će samo biti plus ili minus jedne jedinice ugaonog mernog uređaja sposobnog za rešavanje.^[30]

Dvodimenzionalni Grejev kod[uredi | uredi izvor]

Dvodimenzionalni Grejevi kodovi se koriste u komunikaciji kako bi se smanjio broj bit-nih grešaka u Kvadraturi amplitudnih modulacija susednih tačaka u Konstelaciskom dijagramu . U tipičnom kodiranju horizontalnih i vertikalnih susednih dijagrama tačaka razlikuju se po jednom bitu, i dijagonalne susedne tačke razlikuju se po 2 bita . ^[31]

Grejeva izometrija[uredi | uredi izvor]

Bijektivno mapiranje{ 0 ↔ 00, 1 ↔ 01, 2 ↔ 11, 3 ↔ 10 } uspostavlja izomeriju između metričkog prostora na krajnjem polju $\mathbb {Z} _{2}^{2}$ sa metričkim datim od Hamingovog rastojanja i metrički prostor tokom krajnjeg prstena $\mathbb {Z} _{4}$ (uobičajeno modul aritmetike) sa metričkim datim od Leeovog rastojanja. Mapiranje je prikladno prošireno na izomerni Hamingov prostor $\mathbb {Z} _{2}^{2m}$ i $\mathbb {Z} _{4}^{m}$ . . Njen značaj leži u uspostavljanju prepiske između " dobrih " vrenosti, ali ne mora da ide linearnim kodeksima, kao Grejeve- mape $\mathbb {Z} _{2}^{2}$ prstenastih linearnih kodova iz $\mathbb {Z} _{4}$ .^[32]^[33]

Vidi još[uredi | uredi izvor]

Linearni povraćaj registrovane smene
De-Bruin redosled
Gilijamov kod
Steinhaus-Džonson-Troterov algoritam, algoritam koji generiše Grejeve kodove za faktorski sistem brojeva

Reference[uredi | uredi izvor]

^ F. Gray.
^ J. Breckman.
^ ^a ^b E. A. Ragland et al.
^ S. Reiner et al.
^ Pickover, Clifford A. (2009). Nedostaje ili je prazan parametar |title= (pomoć)
^ ^a ^b ^v Knuth, Donald E. "Generating all n-tuples."
^ Cattermole, K. W. (1969). Nedostaje ili je prazan parametar |title= (pomoć)
^ Goodall, W. M. (1951). Nedostaje ili je prazan parametar |title= (pomoć)
^ Wakerly, John F (1994). Nedostaje ili je prazan parametar |title= (pomoć)
^ "Synchronization in Digital Logic Circuits by Ryan Donohue
^ Mehta, H.; Owens, R.M. & Irwin, M.J. (1996), Some issues in gray code addressing, in the Proceedings of the 6th Great Lakes Symposium on VLSI (GLSVLSI 96), IEEE Computer Society. pp. 178.
^ The Gray Code by R. W. Doran
^ Henry Gordon Dietz. "The Aggregate Magic Algorithms: Gray Code Conversion"
^ ^a ^b Guan, Dah-Jyh (1998). „Generalized Gray Codes with Applications”. Proc. Natl. Sci. Counc. Repub. Of China (A). 22. CiteSeerX 10.1.1.119.1344 .
^ ^a ^b Bhat, Girish S.; Savage, Carla D. (1996). „Balanced Gray codes”. Electronic Journal of Combinatorics. 3 (1): R25. doi:10.37236/1249.
^ Suparta, I. N. (2005). Nedostaje ili je prazan parametar |title= (pomoć)
^ ^a ^b M. Flahive and B. Bose (2007). Nedostaje ili je prazan parametar |title= (pomoć)
^ ^a ^b C. D Savage and P. Winkler (1995). Nedostaje ili je prazan parametar |title= (pomoć)
^ C. D Savage (1997). Nedostaje ili je prazan parametar |title= (pomoć)
^ ^a ^b Goddyn, Luis (1999).
^ Sawada, J.; Wong, D. (2007). Nedostaje ili je prazan parametar |title= (pomoć)
^ Kautz, W. H. (1958). Nedostaje ili je prazan parametar |title= (pomoć)
^ ^a ^b NZ 264738, Spedding, Norman Bruce, "A position encoder", published 1994 A claim is at http://www.winzurf.co.nz/Single_Track_Grey_Code_Patent/Single_track_Grey_code_encoder_patent.pdf
^ Hiltgen, Alain P.; Paterson, Kenneth G.; Brandestini, Marco (1996). Nedostaje ili je prazan parametar |title= (pomoć)
^ ^a ^b Hiltgen, Alain P.; Paterson, Kenneth G. (septembar 2001). Nedostaje ili je prazan parametar |title= (pomoć)CS1 održavanje: Format datuma (veza)
^ Etzion, Tuvi; Schwartz, Moshe (1999). Nedostaje ili je prazan parametar |title= (pomoć)
^ Torsten Sillke.
^ Etzion, Tuvi; Paterson, Kenneth G. (maj 1996). Nedostaje ili je prazan parametar |title= (pomoć)CS1 održavanje: Format datuma (veza)
^ Ruskey, Frank; Weston, Mark (June 18, 2005). Nedostaje ili je prazan parametar |title= (pomoć)
^ Alciatore, David G.; Histand, Michael B. (1999). Nedostaje ili je prazan parametar |title= (pomoć)
^ comp.dsp | Gray code for QAM
^ Marcus Greferath (2009). Nedostaje ili je prazan parametar |title= (pomoć)
^ Encyclopedia of Mathematics

Literatura[uredi | uredi izvor]

Black, Paul E. Gray code. 25 February 2004. NIST.
Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). „Section 22.3. Gray Codes”. Numerical Recipes: The Art of Scientific Computing (3rd izd.). New York: Cambridge University Press. ISBN 978-0-521-88068-8. Arhivirano iz originala 11. 08. 2011. g. Pristupljeno 21. 11. 2015.
Savage, Carla (1997). „A Survey of Combinatorial Gray Codes”. SIAM Rev. 39 (4): 605—629. Bibcode:1997SIAMR..39..605S. JSTOR 2132693. S2CID 6375360. doi:10.1137/S0036144595295272. Arhivirano iz originala 26. 04. 2007. g. Pristupljeno 21. 11. 2015.
Wilf, Herbert S. (1989). „Chapters 1–3”. Combinatorial algorithms: an update. SIAM. ISBN 978-0-89871-231-5.

Spoljašnje veze[uredi | uredi izvor]

"Gray Code" demonstration by Michael Schreiber, Wolfram Demonstrations Project (sa Metematičkom implementacijom). 2007.
NIST Dictionary of Algorithms and Data Structures: Gray code
Hitch Hiker's Guide to Evolutionary Computation, Q21: What are Gray codes, and why are they used?, uključujući C kod za pretvaranje između binarnih i BRGC
Subsets or Combinations Može da generiše BRGC niz
"The Structure of Single-Track Gray Codes" Arhivirano na sajtu Wayback Machine (10. mart 2007) by Moshe Schwartz, Tuvi Etzion
Single-Track Circuit Codes Arhivirano na sajtu Wayback Machine (7. jun 2011) by Hiltgen, Alain P.; Paterson, Kenneth G.
Dragos A. Harabor koristi „Gray codes in a 3D digitizer”. Arhivirano iz originala 22. 11. 2015. g. Pristupljeno 21. 11. 2015. .
pojedinačna traka Grejevog koda, binarno chain codes (Lancaster 1994), i linear feedback shift registers svi su korisni u pronalaženju nečije apsolutne pozicije na pojedinačnoj traci rotacionog enkodera ( ili nekog drugog senzora položaja ) .
Computing Binary Combinatorial Gray Codes Via Exhaustive Search With SAT Solvers by Zinovik, I.; Kroening, D.; Chebiryak, Y.
AMS Column: Gray codes
Optical Encoder Wheel Generator
ProtoTalk.net – Understanding Quadrature Encoding – Omoti kuadrature kodiranje detaljniji sa fokusom na robotskim aplikacijama

[patent-1] F. Gray.

[pat1-2] J. Breckman.

[pat2-3] E. A. Ragland et al.

[pat3-4] S. Reiner et al.

[5] Pickover, Clifford A. (2009). Nedostaje ili je prazan parametar |title= (pomoć)

[knuth-6] v Knuth, Donald E. "Generating all n-tuples."

[7] Cattermole, K. W. (1969). Nedostaje ili je prazan parametar |title= (pomoć)

[8] Goodall, W. M. (1951). Nedostaje ili je prazan parametar |title= (pomoć)

[9] Wakerly, John F (1994). Nedostaje ili je prazan parametar |title= (pomoć)

[10] "Synchronization in Digital Logic Circuits by Ryan Donohue

[11] Mehta, H.; Owens, R.M. & Irwin, M.J. (1996), Some issues in gray code addressing, in the Proceedings of the 6th Great Lakes Symposium on VLSI (GLSVLSI 96), IEEE Computer Society. pp. 178.

[12] The Gray Code by R. W. Doran

[13] Henry Gordon Dietz. "The Aggregate Magic Algorithms: Gray Code Conversion"

[guan-14] Guan, Dah-Jyh (1998). „Generalized Gray Codes with Applications”. Proc. Natl. Sci. Counc. Repub. Of China (A). 22. CiteSeerX 10.1.1.119.1344 .

[balanced-15] Bhat, Girish S.; Savage, Carla D. (1996). „Balanced Gray codes”. Electronic Journal of Combinatorics. 3 (1): R25. doi:10.37236/1249.

[16] Suparta, I. N. (2005). Nedostaje ili je prazan parametar |title= (pomoć)

[balancing-17] M. Flahive and B. Bose (2007). Nedostaje ili je prazan parametar |title= (pomoć)

[monotone-18] C. D Savage and P. Winkler (1995). Nedostaje ili je prazan parametar |title= (pomoć)

[19] C. D Savage (1997). Nedostaje ili je prazan parametar |title= (pomoć)

[goddyn-20] Goddyn, Luis (1999).

[21] Sawada, J.; Wong, D. (2007). Nedostaje ili je prazan parametar |title= (pomoć)

[22] Kautz, W. H. (1958). Nedostaje ili je prazan parametar |title= (pomoć)

[NBSpedding-23] NZ 264738, Spedding, Norman Bruce, "A position encoder", published 1994 A claim is at http://www.winzurf.co.nz/Single_Track_Grey_Code_Patent/Single_track_Grey_code_encoder_patent.pdf

[HiltPatBrand-24] Hiltgen, Alain P.; Paterson, Kenneth G.; Brandestini, Marco (1996). Nedostaje ili je prazan parametar |title= (pomoć)

[HiltPat-25] Hiltgen, Alain P.; Paterson, Kenneth G. (septembar 2001). Nedostaje ili je prazan parametar |title= (pomoć)CS1 održavanje: Format datuma (veza)

[etzion-26] Etzion, Tuvi; Schwartz, Moshe (1999). Nedostaje ili je prazan parametar |title= (pomoć)

[27] Torsten Sillke.

[EtzPat-28] Etzion, Tuvi; Paterson, Kenneth G. (maj 1996). Nedostaje ili je prazan parametar |title= (pomoć)CS1 održavanje: Format datuma (veza)

[29] Ruskey, Frank; Weston, Mark (June 18, 2005). Nedostaje ili je prazan parametar |title= (pomoć)

[30] Alciatore, David G.; Histand, Michael B. (1999). Nedostaje ili je prazan parametar |title= (pomoć)

[31] .dsp | Gray code for QAM

[Greferath2009-32] Marcus Greferath (2009). Nedostaje ili je prazan parametar |title= (pomoć)

[33] Encyclopedia of Mathematics

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

$P_{n,j}$	j = 0	j = 1	j = 2	j = 3
n = 1	0, 1
n = 2	00, 01	10, 11
n = 3	000, 001	100, 110, 010, 011	101, 111
n = 4	0000, 0001	1000, 1100, 0100, 0110, 0010, 0011	1010, 1011, 1001, 1101, 0101, 0111	1110, 1111