Dekartov pravougli koordinatni sistem

Dekartov pravougli koordinantni sistem u ravni. Četiri tačke su markirane: zelena (2, 3), crvena (-3, 1), plava (-1,5; -2,5) i ljubičastom koordinatni početak (0, 0).

Dekartov koordinanti sistem se koristi u matematici za jednoznačno definisanje položaja tačaka u prostoru. Karakteristika ovog sistema je da su njegove koordinatne ose međusobno normalne.

Dekartov pravougli koordinatni sistem je izmislio francuski matematičar i filozof Rene Dekart, koji je, između ostalih stvari, pokušavao da spoji algebru i Euklidsku geometriju. Ovaj rad je mnogo uticao na razvoj analitičke geometrije, računa i kartografije.

Ideja o ovom sistemu je razvijena 1637. u dva Dekartova dela. U drugom delu svog Metoda predavanja, Dekart je uveo novu ideju određivanja položaja tačke ili predmeta na površini, koristeći dve normalne ose kao pomagalo za merenje. U Geometriji, Dekart je dalje objasnio gore spomenuti koncept.

Istorija

Zasluga za otkriće Kartezijevog koordinatnog sistema pripala je francuskom matematičaru Rene Dekartu (1596—1650) koji ga je imenovao po svojoj latinskoj verziji imena Cartesius. Premda je ideja bila utemeljena još 1637. godine odvojeno u dva zapisa Dekarta i Fermata, potonji nije objavio svoje otkriće. Francuski sveštenik Nikol Oresm koristio je konstrukcije slične Dekartovim dugo pre vremena Dekarta i Fermata. Dekart je uveo novu zamisao određivanja položaja tačke ili objekta u ravni upotrebivši dve međusobno normalne ose kao merila. Otkriće Kartezijevog koordinatnog sistema značilo je veliki napredak u matematici povezujući najprije Euklidsku geometriju i algebru. Kružnice, elipse i druge krive sada su prvi put mogle biti opisivane „kartezijskim” algebarskim jednačinama pomoću koordinata tačaka krive u ravni. Razvoj kartezijevog koordinatnog sistema značajno je doprineo daljnjem razvoju matematike i omogućio Njutnu i Lajbnicu otkriće diferencijalnog i integralnog računa.

Premda je Dekart dao koordinatnom sistemu svoje ime, treba naglasiti da su se slični koordinatni sistemi koristili i pre njega uključivši Abu Rajhan Muhamed ibn Ahmed Birunija, te Persijsku matematiku X i XI veka. Nakon Dekarta razvijeni su i drugi koordinatni sistemi kao što su polarni, sferični, cilindrični i drugi.

Dekartov koordinatni sistem

Nalik zemljopisnoj karti gde je položaj nekog mesta određen s dva podatka: zemljopisnom širinom i zemljopisnom dužinom, nacrtaju li se dva međusobno normalna brojevna pravca, na primer x i y - uobičajeno x horizontalan, a y vertikalan, koji se seku u tačci O i odrede li se na pravcima x i y jedinične tačke E i F, tako da je /OE/=/OF/=1, time je definisan pravougaoni ili Kartezijev koordinatni sistem u ravni.

Dekartov koordinatni sistem se može koristiti u prostoru (gde se koriste tri koordinate: x, y i z) i u višedimenzionalnim sistemima.

Dekartov koordinatni sistem u ravni

Raspored kvadranta

Dvodimenzioni Dekartov koordinatni sistem se koristi da jednoznačno odredi svaku tačku u ravni pomoću dva broja, koji se obično označavaju sa x i y. Dekartov koordinatni sistem je definisan sa dve ose (x-osa ili apscisa i y-osa ili ordinata). Izborom mere za svaku osu i označavanjem jedinica mere duž osa formira se skala.

Dekartov koordinatni sistem sa krugom poluprečnika 2. Jednačina kruga je x² + y² = 4.

Korišćenjem Dekartovog koordinatnog sistema geometrijske figure (kao što su krive) se mogu iskazati algebarskim jednačinama, tj. jednačinama koje zadovoljavaju koordinate na tačkama koje leže na figuri. Na primer, krug poluprečnika 2 se može prikazati formulom x² + y² = 4.

Trodimenzionalni Dekartov koordinatni sistem

Ilustracija Dekartovog koordinatnog sistema u 3D

Kartezijev koordinatni sistem se može izabrati i kao o jednodimenzionalni matematički prostor, gde će takav prostor biti određen jednom osom uz izbor orentacije ose i jedinične dužine, a koordinata (jedna) će u tom slučaju određivati položaj tačke na brojevnom pravcu koji je pridružen koordinatnoj osi.

Raspored oktanta u 3D sistemu

Kartezijev dvodimenzionalni koordinatni sistem određuje položaj tačke u ravni, a kartezijev trodimenzionalni koordinatni sistem određuje položaj tačke u prostoru gde je takav koordinatni sistem definisan središtem koordinatnog sistema 0, i tri oijentirane ose (x, y i z) s odgovarajućim jediničnim dužinama. Koordinate svake tačke u takvom sistemu zadate su uređenim skupom od 3 broja, na primer (3, -1, 5) koji označavaju odgovarajuće koordinate u trodimenzionalnom matematičkom prostoru, gde su koordinate predstavljene orijentisanim normalnim udaljenostima od neke tačke do odgovarajuće ravni. U trodimenzionalnom koordinatnom sistemu nazivi osa (apscisa i ordinata) nisu mandatorne, ali ako se upotrebljavaju tada je uobičajeno da se treća, z osa, nazvati aplikata. Na isti način je uobičajeno da se x i y osa postave u horizontalnu ravan, a preostala z osa normalno na njih. Konačno, trodimenzionalni koordinatni sistem se dili na osam područja, „oktanata”, omeđenih sa odgovarajućim delovim ravni. Prvi oktant je onaj gde su sve tri poluose pozitivne.

Višedimenzionalni Dekartov koordinatni sistem

Sledeći navedeni princip generalno se mogu koordinate tačke odrediti i u n-dimenzionalnom matematičkom prostoru gde će se pomoću n odgovarajućih koordinata definisati orijentisana udaljenost od tačke do jedne od n hiperravni. U četvorodimenzionalnom matematičkom prostoru na primer, postojaće četiri ose x, y, z i w, a koordinate svake tačke u takvom matematičkom prostoru biće određene uređenim skupom od četiri broja.

Neposredne primene i svojstva

Udaljenost između dve tačake u ravni

Udaljenost dve tačke u ravni određena Kartezijevim koordinatama $(x_{1},y_{1})$ i $(x_{2},y_{2})$ je

$d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}.$

što je vid izraza Pitagorine teoreme iskazane u Kartezijevom koordinatnom sistemu.

Središte duži

Neka je dužina zadata tačkama A i B i njihovim koordinatama A$(x_{1},y_{1})$ i B$(x_{2},y_{2})$, tada će središte duži imati koordinate

$x_{p}={\frac {x_{1}+x_{2}}{2}}$ i

$y_{p}={\frac {y_{1}+y_{2}}{2}}$.

Koordinate težišta trougla

Neka je trougao ABC smešten u Kartezijevom koordinatnom sistemu i određen tačkama s koordinatama A$(x_{1},y_{1})$, B$(x_{2},y_{2})$ i C$(x_{3},y_{3})$, tada će težište trougla imati koordinate

$x_{t}={\frac {x_{1}+x_{2}+x_{3}}{3}}$ i

$y_{t}={\frac {y_{1}+y_{2}+y_{3}}{3}}$.

Udaljenost između dve tačke u prostoru

Udaljenost dve tačke u prostoru određene u trodimenzionalnom Kartezijevom koordinatnom sistemu $(x_{1},y_{1},z_{1})$ i $(x_{2},y_{2},z_{2})$ je

$d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}}$

što se može utvrditi primenom Pitagorine teoreme.

Translacija

Skup tačaka u ravni, na primer trougla ABC, može se pomaknuti u ravni uz očuvanje međusobnih udaljenosti i orijentacije uz dodavanje utvrđenog para brojeva (X,Y) Kartezijevim koordinatama svake tačke skupa. Ako su koordinate tačaka trougla A(x’, y’), B(x’’, y’’) i C(x’’’, y’’’) tada će translirani, odn. pomaknuti trougao imati koordinate A’(x’+X, y’+Y), B’(x’’+X, y’’+Y) i C’(x’’’+X, y’’’+Y)

Uvećanje, smanjenje

U Kartezijevim koordinatama neki lik može se učiniti većim ili manjim tako što se sve koordinate svih tačaka pomnože faktorom proporcionalnosti, npr. m. Ako su koordinate tačaka koje određuju dužinu AB, A(x’, y’) i B(x’’, y’’) tada nove koordinate tačaka koje određuju dužinu A’B’ će biti A’(mx’, my’) i B’(mx’’, my’’). Ako je m>1 dobijeni lik će biti veći, a ako je m<1 dobijeni lik će bite manji od izvornog lika.

Dekartov koordinatni sistem sa krugom radijusa 2, čiji centar je u koordinatnom početku.

Prikaz krivih u koordinatnom sistemu u ravni

U Kartezijevom koordinatnom sistemu jednostavno se prikazuju krive u ravni (kružnica, elipsa, parabola i td.) te različite funkcije (linearne, polinomne, eksponencijalne, trigonometrijske i td.).

Prikazujući na primer kružnicu u Kartezijevom koordinatnom sistemu ustanovljava se da za svaku tačku kružnice vredi da je

$x^{2}+y^{2}=r^{2}\,$

te će prema tome jednačkina kružnice poluprečnika 2 (slika desno) biti

$x^{2}+y^{2}=2^{2}\,$

Prikaz vektora u Kartezijevim koordinatama

Tačka u prostoru opisanom Kartezijevim koordinatama može definisati vektor. Vektor pomaka, na primer r, može imati hvatište u išodištu Dekartovog koordinatnog sistema i vrh u tački u prostoru. Strelica koja pokazuje prema vrhu vektora definiše smer vektora (smer pomaka), a ortogonalne projekcije na osi x, y i z odgovarajući pomak u x, y ili z smeru. Dužina samog vektora tada je apsolutna veličina pomaka u prostoru

$|{r}|={\sqrt {(x)^{2}+(y)^{2}+(z)^{2}}}$,

a takođe se može zapisati da je

$\mathbf {r} =x\mathbf {i} +y\mathbf {j} +z\mathbf {k}$,

gde su i, j i k jedinični vektori u smeru x, y i z ose.

Vektor u Kartezijevom trodinemzionalnom prostoru određen je na taj način u celosti uređenim skupom od četiri veličine (r, x, y, z). Ovakav prikaz vektora uveo je Vilijam Rouan Hamilton.

Primene

Svaka osa može u praktičnoj primeni prema potrebi da ima različite merne jedinice (kilograme, sekunde, vate, itd), što znači da se Kartezijevim koordinatnim sistemom mogu prikazivati ne samo krive, lukovi i geometrijska tela u dvodimenzionalnom, odnosno trodimenzionalnom prostoru, već da se mogu prikazivati i sve moguće ostale promenjive (masa, vreme, energija, sila i mnoge druge). Premda je teško vizualizovati četvoro i višedimenzionalne prostore, algebra Kartezijevih koordinata može se jednostavno proširiti na četiri ili više promenljivih tako da se mogu izvršiti proračuni vrednosti funkcija i sa četiri ili više promenljivih. Takva algebra definiše geometriju višedimenzionih prostora.

Značaj

Kartezijeve koordinate su temelj analitičke geometrije i osiguravaju geometrijsku interpretaciju za brojna područja matematike kao što su linearna algebra, kompleksna analiza, diferencijalna geometrija itd. Jedan od najpoznatijih primera je koncept grafičkog prikaza ili grafa funkcije. Kartezijske koordinate su osnovno oruđe u mnogim područjima koja se bave geometrijom uključujući astronomiju, fiziku, tehničke struke, ekonomiju i drugde.

Orijentacija

Dve dimenzije

Pravilo desne ruke

Fiksiranje ili izbor x-ose određuje y-ose sve do pravca. Naime, y-osa je nužno okomita na x-osu kroz tačku označenu 0 na x-osi. Ali postoji izbor koju od dve poluprave na normali označiti kao pozitivnu, a koju kao negativnu. Svaki od ova dva izbora određuje drugačiju orijentaciju kartezijanske ravni.

Uobičajeni način orijentacije ravni, pri čemu je pozitivna x-osa usmerena udesno, a pozitivna y-osa usmerena nagore (x-osa je "prva", a y-osa "druga" osa), smatra se da je pozitivna ili standardna orijentacija, koja se naziva i desnostrana orijentacija.

Često korišćena mnemonika za definisanje pozitivne orijentacije je pravilo desne ruke. Postavljanjem donekle zatvorene desne ruke na ravan sa palcem okrenutim nagore, prsti upiru od x-ose ka y-osi, u pozitivno orijentisanom koordinatnom sistemu. Drugi način orijentacije ravni je praćenje pravila leve ruke, postavljanje leve ruke na ravan sa palcem okrenutim nagore. Kada se palac usmeri od početka duž ose ka pozitivnom, zakrivljenost prstiju ukazuje na pozitivnu rotaciju duž te ose. Bez obzira na pravilo koje se koristi za orijentaciju ravni, rotiranje koordinatnog sistema će sačuvati orijentaciju. Promena bilo koje ose će obrnuti orijentaciju, ali menjanje obe će ostaviti orijentaciju nepromenjenom.

Tri dimenzije

Slika 7 – Leva orijentacija je prikazana na levoj strani, a desnoruka na desnoj strani.

Slika 8 – Desni Dekartov koordinatni sistem koji pokazuje koordinatne ravni

Kada su x- i y-ose specificirane, one određuju liniju duž koje treba da leži z-osa, ali postoje dve moguće orijentacije za ovu liniju. Dva moguća koordinatna sistema, koja rezultiraju, nazivaju se 'desnoruki' i 'levoruki'. Standardna orijentacija, gde je xy ravan horizontalna, a z-osa usmerena nagore (a x- i y-osa formiraju pozitivno orijentisan dvodimenzionalni koordinatni sistem u xy-ravni ako se posmatra odozgo xy-ravni) naziva se desna ili pozitivna.

3D kartezijanske koordinatne orijentacije

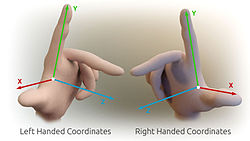
Ime potiče od pravila desne ruke. Ako je kažiprst desne ruke usmeren napred, srednji prst savijen prema unutra pod pravim uglom u odnosu na njega, a palac postavljen pod pravim uglom prema oba, tri prsta označavaju relativnu orijentaciju x-, y-, i z-ose u desnorukom sistemu. Palac označava x-osu, kažiprst y-osu, a srednji prst z-osu. Nasuprot tome, ako se isto uradi levom rukom, nastaje levoruki sistem.

Slika 7 prikazuje levoruki i desnoruki koordinatni sistem. Pošto je trodimenzionalni objekat predstavljen na dvodimenzionalnom ekranu, dolazi do izobličenja i dvosmislenosti. Osa koja je usmerena nadole (i udesno) takođe treba da pokazuje ka posmatraču, dok „srednja“ osa treba da pokazuje dalje od posmatrača. Crveni krug je paralelan sa horizontalnom xy-ravninom i označava rotaciju od x-ose do y-ose (u oba slučaja). Dakle, crvena strelica prolazi ispred z-ose.

Slika 8 je još jedan pokušaj da se prikaže desnoruki koordinatni sistem. Opet, postoji nejasnoća uzrokovana projektovanjem trodimenzionalnog koordinatnog sistema u ravan. Mnogi posmatrači vide sliku 8 kao „prevrtanje“ između konveksne kocke i konkavnog „ugla“. Ovo odgovara dvema mogućim orijentacijama prostora. Gledanje na figuru kao konveksnu daje levoruki koordinatni sistem. Stoga je „tačan“ način da se sagleda slika 8 da se zamisli x-osa kao da je usmerena ka posmatraču i da se tako vidi konkavni ugao.

Predstavljanje vektora u standardnoj bazi

Tačka u prostoru u Dekartovom koordinatnom sistemu takođe može biti predstavljena vektorom položaja, koji se može zamisliti kao strelica koja pokazuje od početka koordinatnog sistema do date tačke. Ako koordinate predstavljaju prostorne pozicije (pomeranja), uobičajeno je da se vektor od početka do tačke interesovanja predstavlja kao $\mathbf {r}$. U dve dimenzije, vektor od koordinatnog početka do tačke sa Dekartovim koordinatama (x, y) se može napisati kao:

$$\mathbf {r} =x\mathbf {i} +y\mathbf {j} ,$$

gde su $\mathbf {i} ={\begin{pmatrix}1\\0\end{pmatrix}}$ i $\mathbf {j} ={\begin{pmatrix}0\\1\end{pmatrix}}$ jedinični vektori u pravcu x-ose i y-ose respektivno, koji se generalno nazivaju standardnom osnovom (u nekim oblastima primene oni se takođe mogu nazivati versori). Slično, u tri dimenzije, vektor od koordinatnog početka do tačke sa Dekartovim koordinatama $(x,y,z)$ se može napisati kao:

$$\mathbf {r} =x\mathbf {i} +y\mathbf {j} +z\mathbf {k} ,$$

gde je $\mathbf {i} ={\begin{pmatrix}1\\0\\0\end{pmatrix}},$ $\mathbf {j} ={\begin{pmatrix}0\\1\\0\end{pmatrix}},$ i $\mathbf {k} ={\begin{pmatrix}0\\0\\1\end{pmatrix}}.$

Ne postoji prirodna interpretacija vektora množenja da bi se dobio drugi vektor koja funkcioniše u svim dimenzijama, ali postoji način da se koriste kompleksni brojevi da se obezbedi takvo množenje. U dvodimenzionalnoj kartezijanskoj ravni, identifikuje se tačka sa koordinatama (x, y) sa kompleksnim brojem z = x + iy. Ovde je i imaginarna jedinica i identifikuje se sa tačkom sa koordinatama (0, 1), tako da nije jedinični vektor u pravcu x-ose. Pošto se kompleksni brojevi mogu pomnožiti dajući drugi kompleksni broj, ova identifikacija pruža sredstvo za „množenje” vektora. U trodimenzionalnom kartezijanskom prostoru slična identifikacija se može izvršiti sa podskupom kvaterniona.

Literatura

• Brennan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1998). Geometry. Cambridge: Cambridge University Press. ISBN 978-0-521-59787-6. 
• Smart, James R. (1998). Modern Geometries (5th Ed). Pacific Grove: Brooks/Cole. ISBN 978-0-534-35188-5. 
• Descartes, René (2001). Discourse on Method, Optics, Geometry, and Meteorology. Trans. by Paul J. Oscamp (Revised izd.). Indianapolis, IN: Hackett Publishing. ISBN 978-0-87220-567-3. OCLC 488633510. 
• Korn, G. A.; Korn, TM (1961). Mathematical Handbook for Scientists and Engineers (1st izd.). New York: McGraw-Hill. str. 55-79. LCCN 59-14456. OCLC 19959906. 
• Margenau, Henry; Murphy, GM (1956). The Mathematics of Physics and Chemistry. New York: D. van Nostrand. LCCN 55-10911. 
• Moon, P.; Spencer, DE (1988). „Rectangular Coordinates (x, y, z)”. Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd, 3rd print izd.). New York: Springer-Verlag. str. 9—11 (Table 1.01). ISBN 978-0-387-18430-2. 
• Morse, Philip M. Herman Feshbach (1953). Methods of Theoretical Physics, Part I. New York: McGraw-Hill. ISBN 978-0-07-043316-8. LCCN 52-11515. 
• Sauer, R.; Szabó, I (1967). Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. LCCN 67-25285. 
• Axler, Sheldon (2015). Linear Algebra Done Right. Undergraduate Texts in Mathematics. Springer. ISBN 978-3-319-11079-0. doi:10.1007/978-3-319-11080-6. Arhivirano iz originala 27. 5. 2022. g. Pristupljeno 17. 4. 2022. CS1 održavanje: Format datuma (veza)
• Berlinski, David (2011). A Tour of the Calculus. Knopf Doubleday Publishing Group. ISBN 9780307789730. 
• Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1998). Geometry. Cambridge: Cambridge University Press. ISBN 978-0-521-59787-6. 
• Burton, David M. (2011). The History of Mathematics/An Introduction (7th izd.). New York: McGraw-Hill. ISBN 978-0-07-338315-6. 
• Griffiths, David J. (1999). Introduction to Electrodynamics. Prentice Hall. ISBN 978-0-13-805326-0. 
• Hughes-Hallett, Deborah; McCallum, William G.; Gleason, Andrew M. (2013). Calculus: Single and Multivariable (6th izd.). John Wiley & Sons. ISBN 978-0470-88861-2. 
• Kent, Alexander J.; Vujakovic, Peter (2017-10-04). The Routledge Handbook of Mapping and Cartography (na jeziku: engleski). Routledge. ISBN 9781317568216. 
• Anton, Howard; Bivens, Irl C.; Davis, Stephen (2021). Calculus: Multivariable. John Wiley & Sons. str. 657. ISBN 978-1-119-77798-4. 

Spoljašnje veze

• Cartesian Coordinate System
• Printable Cartesian Coordinates
• MathWorld description of Cartesian coordinates
• „Cartesian coordinates”. PlanetMath. 
• Coordinate Converter – converts between polar, Cartesian and spherical coordinates
• Coordinates of a point Interactive tool to explore coordinates of a point
• open source JavaScript class for 2D/3D Cartesian coordinate system manipulation