Питагорина теорема

У математици, Питагорина теорема изражава везу која постоји између три странице правоуглог троугла у еуклидској геометрији. Ако су a и b катете, а c хипотенуза правоуглог троугла, важи једнакост
односно, исказано речима:
Површина квадрата конструисаног над хипотенузом правоуглог троугла једнака је збиру површина квадрата конструисаних над катетама тог троугла.
Теорема је добила име према старогрчком математичару Питагори, за кога се, традиционално, сматра да ју је открио и доказао,[1] иако је данас извесно да је била позната много пре Питагоре.[2][3]
Питагорина теорема је једна од основних и најзначајнијих математичких теорема. Препознатљива слика правоуглог троугла са конструисаним квадратима над све три странице, коришћена за визуелни приказ самог тврђења, послужила је као основа за генерисање фрактала који се назива Питагорино дрво.
Историја[уреди | уреди извор]

Историјски посматрано, откриће и разумевање Питагорине теореме је прошло кроз неколико етапа:
- алгебарско истраживање постојања Питагориних тројки,
- боље упознавање односа између страница правоуглог троугла, односно односа између суседних углова троугла, које је последица стицања све већих знања о равнима и површима и
- налажење великог броја различитих доказа теореме.
Древне цивилизације[уреди | уреди извор]
Веза која постоји између страница троугла чије су дужине 3, 4 и 5 била је позната још Вавилонцима, 2000. п. н. е.[4] а може се наћи и у чувеној кинеској књизи Девет књига о математичкој вештини за коју се претпоставља да је написана око 1100. п. н. е.[5]
Чувена вавилонска глинена плочица која носи број 322 у колекцији Плимптона је таблица Питагориних тројки са 15 редова настала 1800. п. н. е. Стари Египћани су знали за четири Питагорине тројке, о чему сведочи папирус датиран у време владавине XII династије, око 2000. п. н. е. у коме је, између осталог, могуће наћи и релацију
- .[5]
Она је еквивалентна Питагориној тројки (3, 4, 5) ако се израз прошири да би се ослободио од разломака.
Питагорине тројке могу се наћи и у Сулвасутрама, светим песмама Хиндуса, из периода 5 — 4. век п. н. е, које говоре о начину добијања правих углова помоћу ужета са 3-4-5, односно 12-16-20, 15-20-25, 5-12-13, 15-36-39, 8-15-17 и 12-35-37 чворова везаних на једнаким растојањима. Коришћење конопца за одређивање правог угла имало је у давна времена своју практичну примену у нпр. парцелисању земљишта, а људи који су се тиме бавили називани су затезачима конопца (грч. Λρπεδονάπται, harpedonaptai).[6] Међутим, према неким ауторима, мало је вероватно да су Египћани заиста користили уже са 12 чворова за одређивање правог угла, и нема очигледних доказа да су знали да је троугао са страницама (3, 4, 5) правоугли.[7]
Питагора[уреди | уреди извор]
Традиционално, откриће теореме се приписује Питагори, старогрчком филозофу и научнику, о коме се данас зна посредно, преко каснијих извора. Према њима, Питагора је рођен око 570. п. н. е. на острву Самос, вероватно је био Талесов ученик, а један део свог живота провео је путујући Египтом и Персијом, да би се, по повратку на родни Самос, сусрео са тиранском владавином Поликрата, што је, сматра се, био разлог да се пресели у Кротон где је основао чувену Питагорејску школу.[8] Питагорејци су тврдили да је теорему открио управо Питагора, и да је, у знак захвалности, жртвовао боговима стотину бикова.[9] Проблем са прецизним утврђивањем праве истине је последица чињенице да су Питагорејци преносили усменим путем стечена знања која су сматрана светим и строго су чувана. Поред тога, често су се нова открића приписивала великом учитељу, док је прави проналазач остајао непознат. У прилог томе стоји чињеница да се у исказу теореме који се појављује у Еуклидовим Елементима нигде не спомиње Питагорино име.[10] Данас постоји неколико хипотеза:
- Питагора је преузео теорему од Вавилонаца, односно само је био посредник између знања која су долазила са Истока и Грка. Иако је, према античким изворима, Питагора посетио Египат и Вавилон, те информације нису поуздане.
- Питагора је формулисао и по први пут доказао теорему независно од вавилонских извора. Овај приступ је био широко прихваћен у древна времена.
- Питагора је за теорему чуо на својим путовањима, али је био први човек који је и доказао. Сасвим је јасно да ни Египћани ни Вавилонци нису ишли даље од свакодневне примене теореме у практичне сврхе. На пример, у Каирском папирусу, откривеном 1938. године, и дешифрованом 1962. године, налази се 40 математичких задатака од којих је девет решено употребом Питагорине теореме. Један од тих задатака гласи:
- „Мердевине дугачке 10 лаката наслоњене су на зид тако да је њихово подножје удаљено 6 лаката од ивице зида. До које висине се пружају те мердевине?“
- Међутим, иако се при решавању проблема користи теорема, нема покушаја да се она уопшти, нити да се докаже.[11]
- Питагора није учествовао у открићу теореме, већ су први доказ нашли његови ученици.[12]
Прво сачувано дело у коме се Питагора повезује са исказом теореме је Плутархов Етички зборник - Моралија, написан крајем првог или почетком другог века н. е. У њему се цитирају стихови из једног несачуваног Аполодоровог дела из другог века п. н. е. Према Плутарху,
када је Питагора открио тај чувени став,
због тога је понудио сјајну жртву волова.
Исте стихове наводи и Атенај из Неукратиса, у свом делу Гозба учених, почетком трећег века н. е.[13]
Следбеници[уреди | уреди извор]
Први писани доказ Питагорине теореме појављује се тек 150 година касније, у првој и шестој књизи Еуклидових Елемената, при чему је, према Проклу, доказ из шесте књиге једини оригинални Еуклидов доказ у Елементима, док је доказ из прве књиге приписан Еудоксу.[10]
Око 250. п. н. е. Архимед апроксимира вредност броја пи користећи Питагорину теорему и уписане и описане полигоне у круг. У 2. веку п. н. е, Клаудије Птолемеј у свом Алмагесту доказује теорему:
- „Производ дијагонала тетивног четвороугла једнак је збиру производа његових наспрамних ивица.“[14]
Одавде се, у специјалном случају када је тетивни четвороугао у ствари правоугаоник, добија Питагорина теорема.
Херон из Александрије је касније[15] доказао формулу којом се може израчунати површина произвољног троугла преко његових страница коришћењем пропорција. Данас се та формула доказује коришћењем Питагорине теореме.
У 3. веку н. е. Папос доказује проширену верзију Питагорине теореме која важи за произвољан троугао, а шест векова касније, Ал Харани даје доказ још једне генерализације која је примењива на произвољан троугао.
Формулација теореме[уреди | уреди извор]

Према теореми:
У било ком правоуглом троуглу, површина квадрата конструисаног над хипотенузом (страницом која се налази насупрот правог угла) је једнака збиру површина квадрата конструисаних над катетама (страницама које се сустичу у правом углу троугла).
Овај исказ се обично наводи у следећем облику:
Квадрат над хипотенузом једнак је збиру квадрата над катетама.
Уколико је са c означена дужина хипотенузе, а са a и b дужине преостале две странице, теорема се може записати помоћу следеће једнакости:
или, ако се одатле изрази c:
Ако је хипотенуза c позната, а треба одредити једну од катета, могуће је користити неку од следеће две једнакости (које се добијају из полазне једнакости, решавањем по одговарајућој непознатој):
или
Из наведених једнакости може се приметити да је веза између страница правоуглог троугла таква да, у случају да је једна од њих непознате дужине, може се одредити помоћу преостале две познате странице. Генерализација ове теореме, позната као косинусна теорема, омогућава израчунавање дужине треће странице произвољног троугла, уколико су познате дужине преостале две странице и величина угла које оне захватају, што је једна од поставки задатка који се назива решавање троугла. Уколико познате странице одређују прав угао, косинусна теорема се своди на Питагорину теорему.
Нееуклидске геометрије[уреди | уреди извор]

У сферној геометрији, на јединичној сфери, за правоугли сферни троугао ABC коме су дужине страница редом a, b и c, Питагорина теорема има облик
Уколико је полупречник сфере дужине , једнакост постаје
У хиперболичкој равни представљеној Поенкареовим моделом диска, уколико је троугао ABC правоугли са катетама a, b и хипотенузом c, Питагорина теорема има облик
при чему је хиперболички косинус дефинисан са
Хилбертови простори[уреди | уреди извор]
Уобичајена норма на реалном еуклидском простору се уводи помоћу скаларног производа. Векторски простор са нормом уведеном помоћу скаларног производа се назива пред-Хилбертовим простором. Ако је пред-Хилбертов простор комплетан у односу на своју метрику, назива се Хилбертовим простором. Ово је увек случај у коначнодимензионим просторима какав је , али бесконачнодимензиони пред-Хилбертови простори не морају бити Хилбертови.
Уколико је у реалном простору са скаларним производом (пред-Хилбертовом простору) уведена норма вектора са
- ,
уз одговарајуће особине[19], онда за ортогоналне векторе и Питагорина теорема добија облик
- .[20]
Докази[уреди | уреди извор]
Питагорина теорема је вековима служила као инспирација за нове математичке доказе, које су проналазили и људи који нису били професионални математичари. У књизи Питагорино тврђење (енгл. The Pythagorean Proposition) Илише Скота Лумиса (енгл. Elisha Scott Loomis), изворно објављеној 1927. године, која је допуњена новим доказима 1940. године, могуће је наћи све познате доказе до њеног објављивања, укупно њих 371. Између осталих ту су наведени Питагорин и Еуклидов доказ, затим најкраћи и најдужи доказ који се приписују Лежандру, Птолемејев, Леонардов, Хајгенсов и Лајбницов доказ као и доказ Џејмса Гарфилда, из времена пре него што је постао председник САД.[21]
Питагорин доказ[уреди | уреди извор]
Иако постоје материјални докази да је веза између катета и хипотенузе правоуглог троугла била позната још древним цивилизацијама, оно што је одлучило да теорема понесе Питагорино име је чињеница да ју је он први доказао. Међутим, како у његово време није било адекватног материјала за записивање, стечена знања су се код питагорејаца преносила усменим путем, те не постоји поуздан извор на основу кога би са сигурношћу могло да се тврди како је изгледао оригинални Питагорин доказ. Еуклид је у својим Елементима дао два доказа теореме, најпре у првој књизи,[22] доказ који се у потпуности заснива на односима површина, а затим и у шестој књизи,[23] доказ који користи сличност и знатно је једноставнији. С обзиром да геометрија у време Питагоре није била довољно развијена, мало је вероватно да је он користио први доказ, а ако је користио други, онда он није био комплетан, пошто је потпуну теорију сразмерности дао тек Еудокс, који је живео два века после Питагоре. Са друге стране, врло је вероватно да је Питагора најпре доказао теорему у случају једнакокраког правоуглог троугла, пошто је тај доказ био познат још Хиндусима, те га је могао чути на својим путовањима по Медитерану. Да ли је доказао и општи случај није познато, али се претпоставља да га је разматрао. Традиционално му се приписује доказ општег случаја који је био познат још у древној Кини.[21]
Еуклидови докази[уреди | уреди извор]
У својим Елементима Еуклид доказује Питагорину теорему на два места, најпре у првој, а затим и у шестој књизи. Први доказ је прилично захтеван за праћење, и према Проклу, припада Еуклидовом претходнику Еудоксу, као и теорија пропорционалности изложена у петој књизи Елемената.[21] Постоје различита тумачења зашто је Еуклид изабрао да у првој књизи теорему докаже на тежи начин, иако су у његово време били познати једноставнији докази. Са једне стране, већина тих доказа је подразумевала поделу правоуглог троугла на мање, сличне троуглове и коришћење особина пропорционалности за извођење одговарајуће једнакости, али оне су изложене тек у петој књизи, док је сличност обухваћена шестом књигом. Са друге стране, како су стари Грци све аритметичке операције интерпретирали кроз геометрију, врло је вероватно да се Еуклиду први доказ природно наметнуо – јер је посматрао Питагорину теорему као однос између површина. Према Проклу, други доказ је у потпуности Еуклидов, штавише, то је једини оригинални Еуклидов доказ у Елементима.[21]

Суштина првог доказа је да, ако су са A, B и C означена темена правоуглог троугла са правим углом код темена A, и ако се из тог темена спусти висина на хипотенузу која се продужи до наспрамне странице квадрата над хипотенузом, она ће поделити тај квадрат на два правоугаоника, чије ће површине бити једнаке површинама квадрата над ближом катетом.
За формалан доказ, најпре је потребно показати да важе следеће елементарне леме:
- (СУС став према подударности троуглова) Ако су две странице једног троугла једнаке са две странице другог троугла, и ако су углови које захватају ти парови једнаких страница такође једнаки, онда су троуглови подударни.[24]
- Површина троугла је једнака половини површине било ког паралелограма конструисаног над двема страницама тог троугла.[25]
- Површина било ког правоугаоника једнака је производу две суседне странице.
- Површина било ког квадрата једнака је производу две његове странице (следи из претходне леме).
Интуитивна идеја доказа је да се квадрати над катетама трансформишу у паралелограме исте површине, који се затим новом трансформацијом уклапају у правоугаонике на које је подељен квадрат над хипотенузом.[26]

- Нека је ACB правоугли троугао са правим углом код темена A.
- На свакој од страница BC, AB и CA нацртани су квадрати CBDE, BAGF и ACIH респективно.
- Из тачке A спуштена је нормала на страницу BC која је продужена до пресека са страницом DE и уједно је паралелна са BD и CE. Њени пресеци са страницама BC и DE су редом означени са K и L.
- Спајањем тачака C и F, односно A и D, добијају се троуглови BCF и BDA.
- Углови CAB и BAG су прави, па су тачке C, A, и G колинеарне. Слично се закључује за тачке B, A и H.
- Углови CBD и FBA су прави, што значи да је угао ABD једнак углу FBC, пошто су оба једнака збиру правог угла и угла ABC.
- Како је страница AB једнака страници FB, а BD једнака BC, троугао ABD је подударан са троуглом FBC.
- Како су тачке A, K и L колинеарне, правоугаоник BDLK има двоструко већу површину од троугла ABD.
- Како су тачке C, A и G колинеарне, квадрат BAGF има двоструко већу површину од троугла FBC.
- Из претходног следи да правоугаоник BDLK има исту површину као квадрат BAGF, која је једнака AB².
- Слично, могуће је показати да правоугаоник CKLE мора да има исту површину као квадрат ACIH која износи AC².
- Сабирањем добијених једнакости биће AB² + AC² = BD × BK + KL × KC
- Како је BD = KL, важи BD* BK + KL × KC = BD(BK + KC) = BD × BC
- Одатле је AB² + AC² = BC², пошто је CBDE квадрат.
Могуће је да је Еуклид био свестан тежине овог доказа, и да је због тога у шестој књизи доказао мало општији случај Питагорине теореме користећи сличност. Према том тврђењу, код правоуглог троугла, геометријски лик (без ограничења да то мора бити квадрат) конструисан над хипотенузом једнак је по површини збиру површина сличних и слично конструисаних геометријских ликова над катетама.[23]
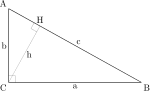
- Нека је ACB правоугли троугао са правим углом код темена C.
- Аналогно претходном доказу, потребно је спустити нормалу из темена правог угла на хипотенузу. Подножје нормале означено је са H.
- Како је AB нормално на CD и AC нормално на CB, углови HAC и HCB су једнаки као углови са нормалним крацима.
- Последица је да су троуглови AHC и CHB међусобно слични, и слични полазном троуглу ACB, па су њихове одговарајуће странице пропорционалне.
- Из једнакости AB/AC=AC/AD и AB/BC=BC/BD, унакрсним множењем добија се да важи AC²=ABxAD и BC²=ABxBD.
- Сабирањем добијених једнакости биће AC²+BC²=ABxAD+ABxBD=ABx(AD+BD)
- Како је AD+BD=AB, важи AC²+BC²=ABxAB=AB².
Поред наведених тврђења, Еуклид је у првој књизи Елемената доказао и тврђење у супротном смеру од Питагорине теореме, према коме је правоугли троугао једини троугао код кога важи једнакост a²+b²=c².[27]
Гарфилдов доказ[уреди | уреди извор]

Још један посебно значајан геометријски доказ, у коме се не користе квадрати над страницама, открио је негде око 1876. године Џејмс Гарфилд, који је касније постао двадесети председник САД. Према Илиши Лумису, доказ је био последица једне Гарфилдове математичке расправе са осталим члановима Конгреса.[21]
Идеја доказа је да се на полазни троугао надовеже још један њему подударан, тако да се краћа катета првог и дужа катета другог налазе на једној правој и да полазе из истог темена. Затим се спајањем преостала два темена троуглова која припадају хипотенузама добија правоугли трапез чије су основице дужине a и b, а висина дужине a+b. Са једне стране, његова површина се може добити као производ полузбира основица и висине, а са друге као збир површина три троугла на које је подељен, па важи:
Леонардов доказ[уреди | уреди извор]


Следећи доказ се приписује чувеном италијанском уметнику и научнику Леонарду да Винчију,[28] а ослања се на симетрију и ротацију.[29]
- Нека је ABC правоугли троугао са правим углом код темена C.
- Над сваком од страница CA, BC и AB конструисани су квадрати ACED, BCFG и ABHJ респективно.
- Над страницом HJ конструисан је троугао HJI који је подударан троуглу ABC, али је у односу на њега заротиран за 180° (степени).
- Шестоугао AJIHBC је преполовљен својом дијагоналом CI.
- Спајањем тачака Е и F добија се шестоугао ABGFED, који је преполовљен својом дијагоналом DG. Троуглови ABC и ECF су симетрични у односу на дијагоналу DG, што за последицу има да су тачке D, C и G колинеарне.
- Ако се четвороугао DABG заротира око тачке A за 90° (у смеру кретања казаљке на сату на приложеној слици), поклопиће се са четвороуглом CAJI, што значи да они имају једнаке површине. То је последица чињенице да су углови DAC и BAJ прави, што значи да је угао DAB једнак углу CAJ, пошто су оба једнака збиру правог угла и угла CAB. Слично, угао AJI је једнак углу ABG, јер су оба једнака збиру правог угла и угла ABC. То значи да дуж AD прелази у AC, дуж AB прелази у AI, а дуж BG у JI.
- Како четвороуглови DABG и CAJI имају једнаке површине (рецимо, S), и шестоуглови ABGFED и AJIHBC имају међусобно једнаке површине (2S). Ако се из шестоугла ABGFED изоставе подударни троуглови ABC и ECF, његова површина се смањује на збир површина квадрата ACED и BCFG. Са друге стране, ако се из површине шестоугла AJIHBC изузму површине подударних троуглова ABC и HJI, добијена површина је једнака површини квадрата ABHJ, а одатле непосредно следи једнакост AC²+BC²=AB².
Доказ Џорџа Ејрија[уреди | уреди извор]

Енглески математичар и астроном, Џорџ Бидел Ејри, свој доказ је формулисао у стиху који је био исписан на пратећој слици, и у оригиналу гласи:
I am, as you can see,
a² + b² - ab
When two triangles on me stand,
Square of hypothenuse is plann'd
But if I stand on them instead
The squares of both sides are read.[30]
што би се могло превести на српски језик са:
- „Ја сам, као што се види, a² + b² - ab. Када на мени стоје два троугла, добија се квадрат над хипотенузом. Али, ако ја стојим на њима добијају се квадрати над катетама.“
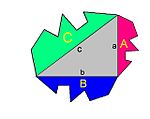
Идеја доказа је да се уочи бели петоугао који је заједнички елемент за обе стране једнакости. На приложеној слици он је добијен тако што су квадрат странице a и квадрат странице b постављени на исту праву и наслоњени један на други, а затим су им одузета два плава правоугла троугла чије су катете дужина a и b. Површина тог петоугла је управо a² + b² - ab. Уколико се на њега надовежу два црвена троугла подударна са плавим троугловима, површина тог другог лика ће бити c² чиме је теорема доказана.
Уопштења теореме[уреди | уреди извор]
Косинусна теорема[уреди | уреди извор]

Једна од значајних генерализација Питагорине теореме је косинусна теорема, која, поред правоуглих, важи и за оштроугле и тупоугле троуглове, односно, може се применити на произвољан троугао. Ако су темена, странице и углови троугла означени као на слици, важе једнакости:
Сабирак вишка се може интерпретирати као двоструки скаларни производ вектора одређених одговарајућим страницама. Када је прав угао, биће , па се тада последња једнакост своди на Питагорину теорему.
Просторна Питагорина теорема[уреди | уреди извор]
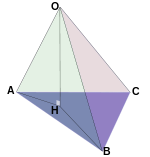
Један просторни аналогон Питагорине теореме је специјалан случај косинусне теореме за тетраедар, према којој, за површине страна тетраедра ABCO означене са , , и , које су наспрамне одговарајућим теменима у свом индексу, и за диедарске углове при ивицама OA (диедарски угао α), OB (β) и OC (γ), важи једнакост:
Ако су углови , и прави, тако да је триедар при темену O правоугли, претходна једнакост се своди на:
што се може сматрати једним уопштењем Питагорине теореме у простору . Ову теорему је француски математичар Жан-Пол де Гија де Малвес презентовао париској Академији наука 1783. године, због чега носи његово име, иако је била позната још Декарту.[33]
Парсевалова једнакост[уреди | уреди извор]
Уопштење Питагорине теореме на бесконачнодимензионим сепарабилним пред-Хилбертовим просторима је познато као Парсевалова једнакост. Ако је један такав простор, а једна његова ортонормална база, тада за сваки вектор важи:
- [20].
Последице и употреба теореме[уреди | уреди извор]
Питагорине тројке[уреди | уреди извор]
Питагорина тројка је уређена тројка природних бројева x, y и z за које важи једнакост x²+y²=z², односно, Питагорину тројку чине целобројне дужине страница правоуглог троугла. Вавилонске глинене таблице[34] (енгл. YBC 7289, Plimpton 322) које су датиране у период 1800—1600. п. н. е. показују да су такве тројке биле познате много пре Питагоре. Данас није најјасније какву су употребну вредност имала та знања. Према неким изворима[35], чини се да је у питању списак готових решења једног проблема који је омогућавао древном предавачу математике да без додатних израчунавања одмах провери тачност ученичких радова.
Свака Питагорина тројка је облика (ka, kb, kc), где је k природан број и (a, b, c) примитивна Питагорина тројка (односно чине је узајамно прости бројеви). Различитих примитивних Питагориних тројки има бесконачно много и позната је њихова експлицитна параметризација.
Геометријска конструкција ирационалних бројева[уреди | уреди извор]
Откриће ирационалних бројева се приписује Питагорејцима, али није прецизно познато да ли су до њих дошли проучавањем геометријске средине или разматрањем дужине дијагонале квадрата.[36] Поред тога што су установили да постоје несамерљиви бројеви, показали су да се они могу конструисати што је озбиљно угрозило њихово веровање да је у основи свега оно што се данас назива рационалним бројем, па је откриће строго чувано. Постоји легенда да је један од чланова братства, који се дрзнуо да јавно говори о томе, за казну утопљен у мору.[37]
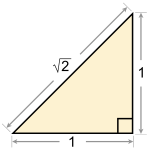
Иако се не могу изразити у облику количника два цела броја, неки ирационални бројеви се могу конструисати помоћу лењира и шестара. Тако се √2, који се понекад назива и Питагорином константом[38], може добити као хипотенуза правоуглог троугла коме су обе катете јединичне дужине. Уколико су катете дужина 1 и √2, хипотенуза ће бити дужине √3 и слично за квадратни корен произвољног природног броја.
Не могу се сви позитивни ирационални бројеви конструисати помоћу лењира и шестара: такви, конструктибилни бројеви чине посебан подскуп скупа алгебарских бројева и стога их има пребројиво много, док је осталих, неконструктибилних реалних бројева непребројиво много; неконструктибилни су, на пример, бројеви , cos 20°, e (Ермит 1871), π (Линдеман 1882), и многи други.
Базелски проблем[уреди | уреди извор]
Италијански математичар Пјетро Менголи је 1644. године поставио питање одређивања збира реципрочних вредности квадрата свих природних бројева. Иако је поставка проблема релативно једноставна, на решење се чекало скоро читав век, јер је тек Ојлер 1735. године објавио резултат, за који је 1741. године и доказао да је заиста тражени збир. Коришћењем математичке нотације, Базелски проблем се може записати на следећи начин:
а збир датог реда се може геометријски апроксимирати коришћењем Питагорине теореме. Конструкцијом правоуглог троугла са катетама дужине 1 и 1/2 добија се хипотенуза чија је дужина квадратни корен збира прва два члана датог реда. Уколико се затим над том хипотенузом као катетом конструише нови правоугли троугао коме је друга катета дужине 1/3, његова хипотенуза ће имати дужину једнаку квадратном корену из збира прва три члана истог реда. Продужавањем поступка у бесконачност дужина хипотенузе сваког следећег троугла је све ближа вредности .
Растојање између две тачке у аналитичкој геометрији[уреди | уреди извор]
Формула за растојање између две тачке у Декартовом правоуглом координатном систему је изведена помоћу Питагорине теореме. Ако су и две тачке у равни, онда је њихово еуклидско растојање:
У општем случају, у вишедимензионом еуклидском простору, растојање између тачака и се одређује формулом:
Фермаова последња теорема[уреди | уреди извор]
Последња Фермаова теорема је тврђење које је Пјер Ферма записао без доказа на маргини Диофантове друге књиге Аритметике, а тиче се питања да ли постоје природни бројеви који би задовољавали уопштење једначине којом се дефинишу Питагорине тројке. Тврђење до кога је дошао отприлике 1637. године,[40] да не постоје природни бројеви a, b и c за које важи једнакост
кад год је n природан број већи од 2, било је вековима претпоставка, а доказао га је тек Ендру Вајлс 1995. године.
Обрнута Питагорина теорема[уреди | уреди извор]
Такозвана Обрнута Питагорина теорема гласи: Ако је површина квадрата конструисаног над хипотенузом једнак збиру површина квадрата конструисаних над катетама, онда је троугао правоугли.
Помињање Питагорине теореме у општој култури[уреди | уреди извор]
У књизи Аутобиографија Бранислав Нушић наводи формулацију теореме у стиху:
Квадрат од хипотенузе,
То зна свако дете,
Раван је квадратима
Од обе катете.[41]
Немачки песник и ботаничар, Аделберт фон Шамисо, посветио је једну своју песму открићу Питагорине теореме.[42]
На једној од седам слика француског сликара Лорана де ла Ера (франц. Laurent de La Hyre) које представљају седам слободних вештина, древни тривијум и квадривијум, под називом Алегорија Геометрије приказана је жена која у десној руци држи пергамент са неколико геометријских слика.[43] Прва у низу је управо слика коју је Еуклид дао у свом доказу Питагорине теореме у првој књизи Елемената.[21]
У филму Виктора Флеминга „Чаробњак из Оза“, снимљеном према истоименој књизи Л. Френка Баума, постоји сцена[44] у којој један од главних јунака, Страшило, у тренутку када добија на поклон од Чаробњака диплому, демонстрира своје знање експлицитно наводећи нетачан исказ теореме у следећем облику:
Збир квадратних корена било које две странице једнакокраког троугла је једнак квадратном корену треће странице.[45]
Страшилову формулацију цитира Хомер Симпсон у десетој епизоди петог серијала серије „Симпсонови“, након што употреби наочари Хенрија Кисинџера нађене у тоалету спрингфилдске нуклеарке. За разлику од Страшиловог исказа који остаје нетачан, у цртаној серији се из позадине чује глас који делимично исправља Хомера („У питању је правоугли троугао, идиоте.“).[46]
У Грчкој, Јапану, Сан Марину, Македонији и Суринаму су издате поштанске марке са карактеристичним визуелним приказом Питагорине теореме.[47]
У Уганди је 2000. године пуштен у оптицај новчић у облику правоуглог троугла, на чијој је задњој страни лик Питагоре и алгебарски запис теореме, уз текст „Питагорин миленијум“.[48]
Карактеристична слика која симболише Питагорину теорему се може видети и на грбу шведског инжењера Кристофера Полхема (швед. Christopher Polhem).[49]
У седамнаестој и тридесет четвртој књизи енглеског издања стрипа Астерикс појављује се лик младог римског архитекте Квадратнадхипотенузиса (енгл. Squareonthehypothenus), чије је име инспирисано теоремом.[50]
Референце[уреди | уреди извор]
- ^ Heath, A History Of Greek Mathematics, volume I, pp. 144
- ^ Миланковић 2017, стр. 19-22.
- ^ Логос 2017, стр. 102 са напоменом 5.
- ^ Андрић 1989, стр. 1.
- ^ а б Smith, History of Mathematics, volume II, pp. 288
- ^ Стројк, Кратак преглед историје математике, pp. 21
- ^ Maor, The Pythagorean Theorem - A 4000 Year History, pp. 15
- ^ Maor, The Pythagorean Theorem - A 4000 Year History, pp. 17.
- ^ Стројк, Кратак преглед историје математике, pp. 52
- ^ а б Maor, The Pythagorean Theorem - A 4000 Year History, pp. 42.
- ^ Burton 2005, стр. 81.
- ^ „Pythagoras - 5. Was Pythagoras a Mathematician or Cosmologist?”. Приступљено 22. 3. 2009.
- ^ Лучић 2009, стр. 97.
- ^ Митровић 1988, стр. 166.
- ^ Због недостатка извора тешко је одредити када се то тачно десило. Према књизи The Pythagorean Theorem - A 4000 Year History у питању је период између 100. п. н. е. и 100. године н. е.
- ^ Дугошија 1999, стр. 84–86.
- ^ Ова једнакост се добија као специјалан случај косинусне теореме за сферни троугао. Уколико се косинусна функција развије помоћу Маклореновог реда, могуће је показати да ће се наведени облик Питагорине теореме приближавати свом еуклидском еквиваленту када полупречник сфере тежи бесконачности.
- ^ Stahl, Saul (1993). „Theorem 8.3”. The Poincaré half-plane: a gateway to modern geometry. Jones & Bartlett Learning. ISBN 978-0-86720-298-4.
За доказ погледати „Sines and cosines in the Poincar´e disk model of the hyperbolic plane” (PDF). стр. 122. Приступљено 24. 2. 2009. - ^ За особине погледати Д. Аднађевић, З. Каделбург,Математичка анализа II, pp. 268
- ^ а б Каделбург 1991, стр. 267–273
- ^ а б в г д ђ Maor, The Pythagorean Theorem - A 4000 Year History
- ^ Еуклид, Елементи, књига I, тврђење XLVII, Приступљено 23. 4. 2013.
- ^ а б Еуклид, Елементи, књига VI, тврђење XXXI, Приступљено 23. 4. 2013.
- ^ Еуклид, Елементи, књига I, тврђење IV, Приступљено 23. 4. 2013.
- ^ Еуклид, Елементи, књига I, тврђење XLI, Приступљено 23. 4. 2013.
- ^ Ради једноставнијег праћења доказа погледати следећи визуелни доказ, трансформацију приказану помоћу јава-аплета, и анимацију.
- ^ Еуклид, Елементи, књига I, тврђење XLVIII, Приступљено 23. 4. 2013.
- ^ Петковић 2006, стр. 212. sfn грешка: више циљева (2×): CITEREFПетковић2006 (help)
- ^ Ради једноставнијег праћења доказа погледати следећу анимацију и архивиранутрансформацију коју је могуће интерактивно направити уз подршку јава-аплета.
- ^ „Још један врло једноставан доказ”. Приступљено 22. 11. 2008.
- ^ Дугошија, Ивановић & Милин 1999, стр. 68.
- ^ „Милорад Бељић, Косинусна теорема за тетраедар” (PDF). Приступљено 23. 10. 2008.
- ^ „de Gua's Theorem”. Приступљено 23. 10. 2008.
- ^ Видети YBC 7289 и Plimpton 322
- ^ „Eleanor Robson, Words and Pictures: New Light on Plimpton 322” (PDF). Приступљено 16. 11. 2008.
- ^ Стројк, Кратак преглед историје математике, pp. 53
- ^ Heath, A History Of Greek Mathematics, volume I, pp. 154.
- ^ Finch 2003, стр. 1.
- ^ Кечкић 1994, стр. 111.
- ^ Синг 1999, стр. 62.
- ^ Нушић 1963, стр. 125, 127.
- ^ Погледати оригинални текст на немачком, и превод на енглески Брајана Кола: „Adalbert von Chamisso, Vom Pythagoreischen Lehrsatz”. Архивирано из оригинала 26. 3. 2012. г. Приступљено 22. 11. 2008.
- ^ „Laurent de La Hyre (1601—1666), Allegory of Geometry”. Архивирано из оригинала 07. 03. 2016. г. Приступљено 16. 11. 2008.
- ^ „Wizard of Oz, Scarecrow's Mathematical Error”. Приступљено 5. 8. 2017.
- ^ „Реплике Страшила из филма „Чаробњак из Оза“”. Приступљено 15. 11. 2008.
- ^ „Реплике Симпсонових из епизоде „$прингфилд“”. Приступљено 15. 11. 2008.
- ^ Miller, Jeff. „Images of Mathematicians on Postage Stamps”. Приступљено 20. 4. 2014.
Погледати поштанске марке издате у Грчкој, Јапану, Сан Марину, Македонији и Суринаму. - ^ „Le Saviez-vous?”. Архивирано из оригинала 21. 9. 2009. г. Приступљено 7. 10. 2008.
- ^ „Christopher Polhem (1661-1751).Swedish engineer, knighted in 1716.”. Приступљено 24. 2. 2009.
- ^ „Squareonthehypothenus”. Архивирано из оригинала 20. 11. 2010. г. Приступљено 20. 2. 2011.
Литература[уреди | уреди извор]
- Stahl, Saul (1993). „Theorem 8.3”. The Poincaré half-plane: a gateway to modern geometry. Jones & Bartlett Learning. стр. 122. ISBN 978-0-86720-298-4.
- Синг, Сајмон (1999). Фермаова последња теорема. Београд: ДН центар. стр. 62. ISBN 978-86-83239-01-6.
- Finch, Steven R. (2003). Mathematical Constants. Cambridge: Cambridge University Press. стр. 1. ISBN 978-0-521-81805-6.
- Петковић, Миодраг (2006). Математички времеплов. Нови Сад: Змај. стр. 212. ISBN 978-86-489-0553-6.
- Maor, Eli (2007). The Pythagorean Theorem - A 4000 Year History. Princeton, New Jersey: Princeton University Press. ISBN 978-0-691-12526-8.
- Стројк, Дирк Ј. (1991). Кратак преглед историје математике. Београд: Завод за уџбенике и наставна средства. ISBN 978-86-17-01779-6.
- Heath, Sir Thomas (1921). A History Of Greek Mathematics, volume I. Oxford: Oxford At The Claredon Press.
- Smith, David Eugene (1953). History of Mathematics, volume II. New York: Dover Publications.
- Петковић, Миодраг (2006). Математички времеплов. Нови Сад: Змај. ISBN 978-86-489-0553-6.
- Андрић, Војислав (1989). Питагорини бројеви. Београд: Архимедес.
- Burton, David M. (2005). The History of Mathematics - An Introduction. McGraw-Hill.
- Лучић, Зоран (2009). Огледи из историје античке геометрије. Београд: Службени гласник. ISBN 978-86-519-0117-4.
- Митровић, Милан; et al. (1988). Геометрија за први разред Математичке гимназије. Београд: Круг. ISBN 978-86-7136-054-8.
- Дугошија, Ђорђе; Ивановић, Живорад; Милин, Лазар (1999). Тригонометрија. Београд: „Круг“. ISBN 978-86-7136-058-6.
- Каделбург, Зоран (1991). Математичка анализа II. Београд: Завод за уџбенике и наставна средства. ISBN 978-86-17-01783-3.
- Кечкић, Јован Д. (1994). Математика са збирком задатака за III разред средње школе. Београд: Завод за уџбенике и наставна средства. стр. 111. ISBN 978-86-17-02963-8.
- Нушић, Бранислав (1963). Аутобиографија. Београд: Новинско-издавачко предузеће „Јеж“. стр. 125,127.
- Миланковић, Милутин (1950). Кроз царство наука. Београд.
- Логос, Александар А. (2017). Путовање мисли : увод у потрагу за истином. Београд.
Спољашње везе[уреди | уреди извор]
- Скуп од 79 различитих доказа Питагорине теореме (језик: енглески)
- Чланак о Питагориној теореми на MathWorld (језик: енглески)
- Еуклидов доказ Питагорине теореме - интерактивна анимација (језик: енглески)
- О једној генерализацији Питагорине теореме - рукопис Е. Дајкстре (језик: енглески)
- Питагорина теорема (језик: српски)
- Да ли ће Питагорина теорема постати Вавилонска теорема (РТС Магазин)




































![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)








