Lagranžova teorema

Ukoliko ste tražili teoremu iz teorije grupa, pogledajte članak Lagranžova teorema (teorija grupa).

Geometrijska interpretacija Lagranžove teoreme

Lagranžova teorema (engl. mean value theorem) je jedna od osnovnih teorema diferencijalnog računa i uopšte matematičke analize. Često se još naziva i teorema o srednjoj vrednosti diferencijalnog računa.

Formulacija

Ako je funkcija f:

• neprekidna na zatvorenom intervalu $\,[a,b]$, i
• diferencijabilna na otvorenom intervalu $\,(a,b)$,

onda postoji tačka $\,c$ iz intervala $\,(a,b)$, takva da je:

${\frac {f(b)-f(a)}{b-a}}=f'(c)$

Dokaz 1

Posmatrajmo funkciju

$h(x)=f(x)+\lambda x$.

I ona je neprekidna na $\,[a,b]$ i diferencijabilna na $\,(a,b)$. Odredimo $\lambda$ za koje funkcija $\,h(x)$ zadovoljava uslove Rolove teoreme.

Dakle, da bi bilo $\,h(a)=h(b)$, mora biti:

$\lambda =-{\frac {f(b)-f(a)}{b-a}}.$

Tada, po uslovima Rolove teoreme, postoji tačka $\,c$ iz intervala $\,(a,b)$, takva da je:

$0=h'(c)=f'(c)+\lambda ,$ te je

$f'(c)={\frac {f(b)-f(a)}{b-a}}.$

Dokaz 2

Posmatrajmo funkciju

$h(x)=f(x)-f(a)-({\frac {f(b)-f(a)}{b-a}})(x-a)$

Kako je funkcija $f$ neprekidna i diferencijablna na intervalu $[a,b]$, odnosno $(a,b)$, i funkcija $h$ je neprekidna i diferencijabilna na istim intervalima. Šta više, $h(a)=h(b)=0$, što znači da na funkciju $h$ možemo primeniti Rolovu teoremu.

Prvi izvod funkcije $h$ je:

$h'(x)=f'(x)-{\frac {f(b)-f(a)}{b-a}}$

Prema Rolovoj teoremi sada sledi da postoji tačka $c$, takva da je $f'(c)=0$, tj.

$0=h'(c)=f'(c)-{\frac {f(b)-f(a)}{b-a}}$,

odnosno:

$f'(c)={\frac {f(b)-f(a)}{b-a}}$,

što je i trebalo da se pokaže.

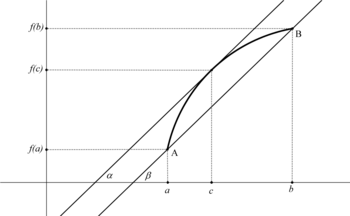
Geometrijska interpretacija

Geometrijska interpretacija: Za bilo koju funkciju neprekidnu na [a, b] i diferencijabilnu na (a, b), postoji tačka c iz intervala (a, b) u kojoj je tangenta (tangent) paralelna sa sečicom (secant) koja povezuje krajeve intervala [a, b].

Geometrijski značaj ove teoreme se sastoji u tome da pod datim uslovima postoji tangenta krive $\,y=f(x)$ u nekoj tački $\,c$, koja pripada zatvorenom intervalu $\,(a,b)$, paralelna sa sečicom koja prolazi kroz tačke $\,A=(a,f(a))$ i $\,B=(b,f(b)).$

Mehanička interpretacija

Ako se tačka kreće po zakonu $\,x=x(t)$, gde je $x(t)$ neprekidna na $[a,b]$ i diferencijablna na $(a,b)$, onda postoji trenutak $\,t_{0}$ u kom je trenutna brzina $x'(t_{0})$ jednaka srednjoj brzini na intervalu $[a,b]$, koja iznosi $\,{\frac {f(b)-f(a)}{b-a}}$, upravo jer postoji to $\,t_{0}$ kada je: $\,f'(t_{0})={\frac {f(b)-f(a)}{b-a}}.$

Posledice i napomene

• Kao ni Rolova teorema, ni Lagranžova teorema nam ne daje informaciju o konstrukciji tačke $\,c$, kao ni o broju takvih tačaka.
• Takođe, posledica Lagranžove teoreme je i sledeće: Ako je za svako $\,x$ iz zatvorenog intervala $\,[a,b]$, $\,f'(x)=0$, onda je funkcija $\,f$ konstantna na zatvorenom intervalu $\,[a,b]$.
• Lagranžova teorema se može posmatrati kao uopštenje Rolove teoreme. Naime, za $\,f(a)=f(b)$, dobijamo funkciju koja ispunjava sve uslove Rolove teoreme.
• Dva važna uopštenja Lagranžove formule, tj. teoreme, su Košijeva teorema i Tejlorova teorema.

Vidi još

• Košijeva teorema
• Tejlorova teorema
• Rolova teorema
• Teoreme srednje vrednosti
• Interval
• Matematička analiza