Методе контурне интеграције
У комплексној анализи, контурна интеграција је метода израчунавања одређених интеграла дуж пута у комплексној равни.[1][2][3]
Контурна интеграција је уско повезана са рачунањем резидума,[4] методологијом комплексне анализе.
Једна од примјена контурне интеграције је рачунање интеграла дуж реалне осе који се не рачунају лако методама са реалним промјењивама.[5]
Контурна интеграција обухвата:
- директно интеграљење комплексне функције дуж криве у комплексној равни (контуре)
- примјена Кошијеве интегралне формуле (КИФ)
- примјена теореме о резидуму.
Може се користити једна метода, или више њих комбиновати.
Директна метода[уреди | уреди извор]
Директне методе обухватају израчунавање интеграла методом сличном онима при израчунавању криволинијског интеграла функција више промјењивих. То значи да користимо сљедећу методу:
- параметризација контуре
- контура се изражава параметарски диференцијалном комплексном функцијом реалне промјењиве, или се прво разбија у више подконтура, а затим се параметризује сваки од њих засебно
- замјена параметарског израза у подинтегрални израз
- замјена параметарског израза у интегралу претвара тај интеграл у интеграл једне реалне промјењиве.
- директно израчунавање
- интеграл се израчунава методама сличним онима у реалној анализи.
Примјер[уреди | уреди извор]
Један од темељних резултата комплексне анализе је чињеница да је контурни интеграл функције z−1 једнак 2πi, при чему је интеграљено по позитивно оријентисаној јединичној кружници (у смјеру обрнутом од казаљке на сату):[а]
При израчунавању овог интеграла, јединичну кружницу |z| = 1 представљамо параметарски са z(t) = eit, t ∈ [0, 2π], при чему dz / dt = i e it па имамо:
што представља вриједност постављеног интеграла.
Примјене интегралних теорема[уреди | уреди извор]
Интегралне теореме се такође користе при израчунавању контурног интеграла, што значи да се реални интеграл израчунава истовремено са контурним.
Интегралне теореме попут Кошијеве интегралне формуле (КИФ) и теореме о резидуму генерално се користе на сљедећи начин:
- одабере се одговарајућа контура
- контура се бира тако да садржи дио реалне осе по којој се израчунава реални интеграл, али и да својом унутрашњошћу обухвата (окружује) сингуларитете, тако да је могуће употријебити КИФ или теорему о резидуму
- примјена теореме Коши-Гурсат
- интеграл се своди на рачунање интеграла само по малим круговима око сваког пола (сваког сингуларитета који је пол)
- примјена КИФ или теореме о резидуму
- примјена ових интегралних формула даје нам вриједност око цијеле контуре
- подјела контуре на реални и имагинарни дио
- цијела контура се може подијелити на дио који обухвата дио реалне осе по ком се првобитно интегралило (назовимо га R) и дио који прелази у имагинарну осу, тј. излази из реалне осе (назовимо га I). Интеграл по цијелој контури једнак је збиру интеграла по свакој од ових подконтура.
- приказивање да који прелази у имагинарну осу не игра никакву улогу у збиру
- ако се за интеграл I може показати да је једнак нули, или у случају да је тражени реални интеграл несвојствен (једна и/или друга граница су бесконачне) да покажемо да интеграл I тежи нули, онда ће вриједност интеграла по R тежити вриједности интеграла по цијелој контури (R+I).
- закључак
- ако можемо обавити горњи корак, можемо директно израчунати интеграл по R, тј. наш реални интеграл.
Примјер (I)[уреди | уреди извор]
Посматрајмо

Да бисмо израчунали овај интеграл, посматрајмо функцију комплексне промјењиве
која има сингуларитете у i и −i. Дакле, изабраћемо контуру која садржи дио реалне осе (јер нам првобитни интеграл у задатку тражи управо рачунање по реалној оси), а затим полукруг као на слици лијево, који ћемо пустити да се шири у бесконачност, тако да ће и онај први дио (који је њен пречник) обухватити цијелу реалну осу (a ће тежити бесконачно). Назовимо ову контуру C.
У овом тренутку имамо два начина да наставимо: користећи КИФ или користећи теорему о резидуму.
Кориштење Кошијеве интегралне формуле (КИФ)[уреди | уреди извор]
Примијетимо да:
па према томе:
Додатно, примијетимо да:
Пошто је једини сингуларитет који се налази унутар ове контуре онај у i, можемо написати
што ставља функцију у облик у којем се директно може примијенити Кошијева интегрална формула. По КИФ је:
(узимамо први извод, у горњим корацима, јер је у питању пол другог реда. Дакле, квадрирали смо (z − i ), помножили са функцијом, а затим од свега тога узели први извод (имплицитно смо га још подијелили са (ред-1)! = (2—1)! = 1! = 1). Да је у функцији било (z − i ) на трећи степен, користили бисмо други извод те дијелили са 2! итд. Случај са полом првог реда, када је (z − i ) на први степен, имали бисмо нулти извод, односно само ƒ(x).)
Ако полукружницу назовемо Luk, треба да докажемо да интеграл по Luk тежи нули када a тежи бесконачности користећи лему о процјени:
гдје је M горње ограничење од |ƒ(z)|, а L дужина од Luk. Сада имамо:
па
Кориштење методе о резидуму[уреди | уреди извор]
Посматрајмо Лоранов развој функције f(z) у околини тачке i, која је једини сингуларитет који нас занима. Имамо дакле:
(Видјети чланак Лоранов развој). Види се да је резидум овдје −i/4 (то је коефицијент уз онај члан полинома са степеном -1, односно гдје је (z-i) степеновано са -1, а то је коефицијент уз израз ). Имамо, дакле, по теореми о резидуму:
Ако назовемо полукружницу Luk треба да покажемо да интеграл по том луку тежи нули када a тежи бесконачности користећи лему о процјени:
гдје је M горње ограничење |f(z)|, а L дужина од Luk. Сад имамо:
Па:
Дакле, добијамо исти резултат као и малоприје.
Напомена за контуру[уреди | уреди извор]
Може се поставити питање да ли бисмо могли направити полукруг око другог сингуларитета, који окружује −i. Да би се интеграл дуж реалне осе кретао у правом смјеру, лук и цијела контура би морали ићи у смјеру обрнутом од казаљке на сату, дакле контура би имала негативну оријентацију, те би цио интеграл промијенио знак.
Ово не утиче на методу рачунања резидума из развоја у ред.
Примјер (II) - Кошијева дистрибуција[уреди | уреди извор]
Интеграл

(који се јавља у теорији вјероватноће као карактеристична функција (односно њен скаларни умножак) [[Кошијева дистрибуција|Кошијеве дистрибуције]) опире се техникама елементарне алгебре. Израчунаћемо га тако што ћемо га изразити као лимес интеграла дуж контуре C која се креће дуж реалне осе од -a до a, а онда у смјеру обрнутом од казаљке на сату дуж полукруга са центром у нули и полупречника a. Нека је a веће од 1, да би имагинарни број i, наш сингуларитет, упадао у унутрашњост криве. Контурни интеграл је:
Пошто је eitz цијела функција (нема сингуларитета нигдје у комплексној равни), онда наша функција има сингуларитете само тамо гдје је именилац z2 + 1 једнак нули. Пошто је z2 + 1 = (z + i)(z − i), то су само тачке z = i и z = −i. Само једна од ових тачака припада нашој контури, а то је i. Резидум функције f(z) у тачки z=i једнак је:
По теореми о резидуму, затим имамо:
Контура C мора бити подијељена у праволинијски и криволинијски дио, тако да
а одатле:
Може се видјети да, ако је t > 0, онда:
Према томе, ако је t > 0, онда:
Слично се може видјети да, ако узмемо контуру која обухвата тачку -i, а не i, видимо да ако је t < 0, онда
и коначно добијамо ово:
(Да је t било једнако нула, онда би се интеграл већ свео на рачун реалне анализе и вриједност тог интеграла била би π.)
Примјер (III) - тригонометријске функције[уреди | уреди извор]
Одређене смјене се могу увести када имамо тригонометријске функције, тако да се интеграл претвори у рационалну функцију комплексне промјењиве, а затим се горње методе могу искористити да се израчуна интеграл.
На примјер, посматрајмо:
Увешћемо смјену z = eit.
Сад, сјетимо се:
и
Узећемо јединични круг да нам буде C, и замјеном добијамо:
Користимо КИФ. Разлажемо именилац на чиниоце:
Сингуларитети су дакле у тачкама 3−1/2i, −3−1/2i. Сад можемо свести интеграл:
гдје је C1 мала кружница око 3−1/2i, а C2 мала кружница око −3−1/2i. Сад можемо искористити формулу:
Примјер (IIIa) — тригонометријски интеграли, општа процедура[уреди | уреди извор]
Горња метода се може примијетнити на интеграле облика
гдје су P и Q полиноми, односно интегрише се рационална функција тригонометријских израза.
Трик у овом случају је да искористимо смјену , при чему је и према томе:
Ова смјена претвара интервал у јединичну кружницу. Штавише:
и
тако да након смјене добијамо неку рационалну функцију ƒ(z) и интеграл постаје:
који се потом рачуна сабирајући све резидуме функције ƒ(z) који се налазе унутар кружнице.
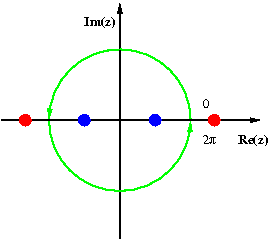
Слика десно илуструје ово за:
који ћемо сада израчунати. Први корак је да примијетимо да
Смјеном добијамо:
Полови ове функције се налазе у 1 ± √2 и −1 ± √2. Од ових, 1 + √2 и −1 −√2 су ван јединичне кружнице (приказани црвеном бојом, није у правој размјери), док се тачке 1 − √2 и −1 + √2 налазе унутар кружнице (плавом бојом). Њима одговарајући резидуми су оба једнаки −i√2/16, тако да је вриједност интеграла:
Примјер (IV) - гране[уреди | уреди извор]
Посматрајмо
Можемо сада почети формулишући комплексни интеграл
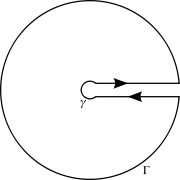
Сада смо опет у ситуацији да бирамо између КИФ и теореме о резидуму да бисмо добили одговарајуће резидуме. Међутим, овдје је важно обратити пажњу да z1/2 = e1/2·Log(z), па z1/2 има „зарез“, јер је вишезначна функција. Ово утиче на наш избор контуре C. Обично се зарез код логаритма дефинише као негативни дио реалне осе, али ово чини интеграљење мало сложенијим, па ћемо изабрати позитивни дио реалне осе.
Потом, узећемо још један мали круг са центром у координатном почетку и полупречника ε нека та кружница не буде потпуна, него нека креће од дужи која се простире паралелно са реалном осом, врло близу али да је не додирује, па около све до исте такве дужи са доње стране реалне осе, која је паралелна са њом и врло је близу, али не додирује реалну осу. Добијамо тако контуру у облику латиничног слова C (познату још шаљиво као „Карнекс“ контура).
Примијетимо да су тачке z = −2 и z = −4 обухваћене већим кругом. Ово су два преостала пола, која се могу добити разлажући именилац на чиниоце. Тачка гранања z = 0 је избјегнута тако што смо окружили око координатног почетка.
Нека је γ тај мали круг полупречника ε, а Γ већи од њих, полупречника r, тада
Пошто је z1/2 = e1/2 Log(z), на контури ван зареза, прелазимо 2π у аргументу преко γ (по Ојлеровој једначини, представља јединични вектор, чији је логаритам онда . Ово је аргумент од z. Коефицијент 1/2 нас тјера да користимо 2); тако:
односно,
а затим:
Може се показати да интеграли по Γ и γ оба теже нули кад ε тежи нули и R тежи бесконачности, користећи процјену, као раније. Тако, имамо:
Користећи теорему о резидуму или Кошијеву интегралну формулу (прво посматрајући контуру као унију једноставнијих контура), добија се:
Види још[уреди | уреди извор]
Напомене[уреди | уреди извор]
- ^ Овдје се умјесто јединичне кружнице могла узети било која Жорданова крива која обухвата нулу, али у нашем примјеру ћемо видјети доказ за јединичну кружницу
Референце[уреди | уреди извор]
- ^ Stalker, John (1998). Complex Analysis: Fundamentals of the Classical Theory of Functions. Springer. стр. 77. ISBN 978-0-8176-4038-5.
- ^ Joseph Bak & Donald J. Newman (1997). Complex Analysis. Springer. Chapters 11 & 12, pp. 130–156. ISBN 978-0-387-94756-3.
- ^ Krantz, Steven George (1999). Handbook of Complex Variables. Springer. Chapter 2. ISBN 978-0-8176-4011-8.
- ^ Mitrinovic, Dragoslav S. & Jovan D. Keckic (1984). The Cauchy Method of Residues: Theory and Applications. Springer. Chapter 2. ISBN 9789027716231.
- ^ Mitrinovic, Dragoslav S. & Jovan D. Keckic (1984). Chapter 5. ISBN 9789027716231.
Литература[уреди | уреди извор]
- Stalker, John (1998). Complex Analysis: Fundamentals of the Classical Theory of Functions. Springer. стр. 77. ISBN 978-0-8176-4038-5.
- Joseph Bak & Donald J. Newman (1997). Complex Analysis. Springer. Chapters 11 & 12, pp. 130–156. ISBN 978-0-387-94756-3.
- Krantz, Steven George (1999). Handbook of Complex Variables. Springer. Chapter 2. ISBN 978-0-8176-4011-8.
- Mitrinovic, Dragoslav S. & Jovan D. Keckic (1984). Chapter 5. ISBN 9789027716231.
- Mitrinovic, Dragoslav S. & Jovan D. Keckic (1984). The Cauchy Method of Residues: Theory and Applications. Springer. Chapter 2. ISBN 9789027716231.


![{\displaystyle {\begin{aligned}\oint _{C}{1 \over z}\,dz&{}=\int _{0}^{2\pi }{1 \over e^{it}}\,ie^{it}\,dt=i\int _{0}^{2\pi }1\,dt\\&{}={\Big [}t{\Big ]}_{0}^{2\pi }i=(2\pi -0)i=2\pi i,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff4c3772d64cc9e2e0e37b3ed8e6d2dfd40dac35)




















































![{\displaystyle [0,2\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/348d40bf3f8b7e1c00c4346440d7e2e4f0cc9b91)

















