Призма (геометријска фигура)
| Скуп униформних n-гоналних призми | |
|---|---|
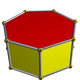
 Пример униформне хексагоналне призме | |
| Type | Униформна у смислу полуправилног полиедра |
| Стране | 2 n-гонална регуларна полигона n квадрата |
| Ивице | 3n |
| Темена | 2n |
| Конфигурација темена | 4.4.n |
| Шлафлијев симбол | {n}×{} [1] t{2, n} |
| Конвејова нотација | Pn |
| Кокстеров дијаграм | |
| Група симетрије | Dnh, [n,2], (*n22), ред 4n |
| Група ротације | Dn, [n,2]+, (n22), ред 2n |
| Дуални полиедар | Конвексна дуална-униформна n-гонална бипирамида |
| Својства | конвексна, регуларна полигонска лица, темено-транзитивне, транслиране основе, стране ⊥ базе |
| Мрежа | |
 | |
Призма је геометријски полиедар ограничен са две паралелне подударне основе (основа може бити било који многоугао) које су повезане паралелограмима (бочним странама). У зависности од многоугла у основи, призма може бити троугаона, четвороугаона, петоугаона итд. Сви попречни пресеци паралелни са основама су транслације основа. Призме су назване по својим основама, нпр. призма са петоугаоном основом назива се петоугаона призма. Призме су подкласа призматоида.
Као и многи основни геометријски термини, реч призма (од грчки πρίσμα (призма) са значењем „нешто тестерисано”) први пут је употребљена у Еуклидовим елементима. Еуклид је дефинисао термин у Књизи XI као „чврста фигура коју ограничавају две супротне, једнаке и паралелне равни, док су остале паралелограми“. Међутим, ова дефиниција је критикована јер није довољно конкретна у односу на природу основа, што је изазвало забуну међу каснијим писцима геометрије.[2][3]
Десна призма, једнолична призма[уреди | уреди извор]

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
|

|

|

|
Десна призма[уреди | уреди извор]
Права призма је призма у којој су спојне ивице и лица окомите на основне површине.[4] Ово важи ако су све спојне површине правоугаоне.
Дуал праве n-призме је права n-бипирамида.
Десна призма (са правоугаоним страницама) са правилним n-угаоним основама има Шафлијев симбол { }×{n}. Она се приближава цилиндричном чврстом телу како се n приближава бесконачности.
Посебни случајеви[уреди | уреди извор]
- Права правоугаона призма (са правоугаоном основом) се такође назива кубоид, или неформално правоугаона кутија. Правоугаона призма има Шафлијев симбол { }×{ }×{ }.
- Права квадратна призма (са квадратном основом) се такође назива квадратни кубоид или неформално квадратна кутија.
Напомена: неки текстови могу применити термин правоугаона призма или квадратна призма и на праву правоугаону призму и на праву квадратну призму.
Униформна призма[уреди | уреди извор]
Униформна призма или полуправилна призма је права призма са правилним основама и квадратним страницама, пошто су такве призме у скупу униформних полиедара.
Униформна n-угаона призма има Шафлијев симбол t{2,n}.
Десне призме са правилним основама и једнаким дужинама ивица формирају један од два бесконачна низа полуправилних полиедара, док су друге серије антипризме.
Подела[уреди | уреди извор]
- Праве и косе призме
- Тростране, четворостране, петостране ...
- Правилне и неправилне
Правилна призма је она призма која у основи има правилан многоугао (троугао, четвороугао, петоугао итд.)
Делови призме[уреди | уреди извор]
- Права
- Основа (Basis)
- Бочна страна
- Основна ивица
Површина призме[уреди | уреди извор]
Површина призме је збир површина свих страна призме. Најједноставније је израчунати површину бочних страна -М- призме и саберемо са две основе.
где је B површина основе, h висина, а P обим основе.
Површина праве призме чија је основа правилан n-страни многоугао са дужином странице s и висином h је према томе:
Запремина призме[уреди | уреди извор]
Запремину призме израчунавамо тако што површину основе призме помножимо висином призме.
где је B површина основе, а h висина. Запремина призме чија је основа n-страни правилан многоугао са дужином странице с је према томе:
Шлегелови дијаграми[уреди | уреди извор]
 P3 |
 P4 |
 P5 |
 P6 |
 P7 |
 P8 |
Симетрија[уреди | уреди извор]
Група симетрије праве n-стране призме са правилном основом је Dnh реда 4n, осим у случају коцке, која има већу групу симетрије Oh реда 48, која има три верзије D4h као подгрупе. Ротациона група је Dn реда 2n, осим у случају коцке, која има већу групу симетрије О реда 24, која има три верзије D4 као подгрупе.
Група симетрије Dnh садржи инверзију ако је n парно.
Хозоедри и диедри такође поседују симетрију диедра, а n-угаона призма се може конструисати геометријским скраћењем n-угаоног хозоедра, као и кроз кантелацију или проширење n-угаоног диедра.
Скраћена призма[уреди | уреди извор]
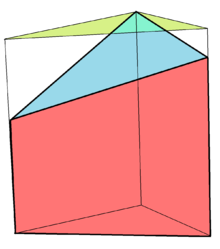
Скраћена призма је призма са непаралелним горњим и доњим странама.[5]
Уврнута призма[уреди | уреди извор]
Уврнута призма је неконвексни полиедар конструисан од униформне n-призме са сваком бочном плочом подељеном на половину квадратне дијагонале, увртањем врха, обично за π/n радијана (180/n степени) у истом правцу, што доводи до конкавних страница.[6]<ref>„Pictures of Twisted Prisms”.
Уврнута призма се не може сецирати на тетраедре без додавања нових врхова. Најмањи случај: троугласти облик, назива се Шенхартов полиедар.
n-угаона уврнута призма је тополошки идентична n-угаоној униформној антипризми, али има половину групе симетрије: Dn, [n,2]+, реда 2n. Може се посматрати као неконвексна антипризма, са тетраедрима уклоњеним између парова троуглова.
| 3-гонал | 4-гонал | 12-гонал | |
|---|---|---|---|
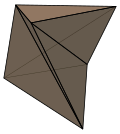 Шенхартов полиедар |
 Уврнута квадратна призма |
 Квадратна антипризма |
 Уврнута додекагонална антипризма |
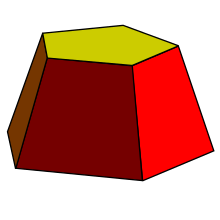
Фрустум[уреди | уреди извор]
Фрустум је конструкција слична призми, са трапезним бочним странама и различитим великим горњим и доњим полигонима.
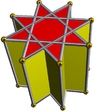
Звездана призма[уреди | уреди извор]
Звездана призма је неконвексни полиедар конструисан од две идентичне површине звездастог полигона на врху и дну, паралелне и померене растојањем и повезане правоугаоним површинама. Униформна звездана призма ће имати Шлафлијев симбол {p/q} × { }, са p правоугаоником и 2 {p/q} лица. Тополошки је идентична p-гоналној призми.
| { }×{ }180×{ } | ta{3}×{ } | {5/2}×{ } | {7/2}×{ } | {7/3}×{ } | {8/3}×{ } | |
|---|---|---|---|---|---|---|
| D2h, ред 8 | D3h, ред 12 | D5h, ред 20 | D7h, ред 28 | D8h, ред 32 | ||

|

|

|

|

|

|
|
Укрштена призма[уреди | уреди извор]
Укрштена призма је неконвексни полиедар конструисан од призме, где су врхови једне основе обрнути око центра ове основе (или ротирани за 180°). Ово трансформише бочне правоугаоне површине у укрштене правоугаонике. За правилну полигонску основу, изглед је n-гонални пешчани часовник. Све косе ивице пролазе кроз један центар тела. Напомена: ниједан врх није у центру овог тела. Укрштена призма је тополошки идентична n-угаоној призми.
| { }×{ }180×{ }180 | ta{3}×{ }180 | {3}×{ }180 | {4}×{ }180 | {5}×{ }180 | {5/2}×{ }180 | {6}×{ }180 | |
|---|---|---|---|---|---|---|---|
| D2h, ред 8 | D3d, ред 12 | D4h, ред 16 | D5d, ред 20 | D6d, ред 24 | |||

|

|

|

|

|

|

|

|
Тороидна призма[уреди | уреди извор]
Тороидна призма је неконвексни полиедар попут укрштене призме, али без доње и горње основне површине, и са једноставним правоугаоним бочним странама које затварају полиедар. Ово се може урадити само за једностране основне полигоне. То су тополошки толози, са Ојлеровом карактеристиком за нулу. Тополошка полиедарска мрежа може бити исечена из два реда квадратних плочица (са конфигурацијом темена 4.4.4.4): трака од n квадрата, од којих је сваки причвршћен за укрштени правоугаоник. n-угаона тороидна призма има 2n врхова, 2n лица: n квадрата и n укрштених правоугаоника и 4n ивица. Тополошки је самодуална.
| D4h, ред 16 | D6h, ред 24 |
| v=8, e=16, f=8 | v=12, e=24, f=12 |

|

|
Призматични политоп[уреди | уреди извор]
Призматични политоп је вишедимензионална генерализација призме. n-димензионални призматични политоп је конструисан од два (n − 1)-димензионална политопа, преведена у следећу димензију.
Призматични n-политопни елементи се удвостручују од (n − 1)-политопских елемената и затим креирају нове елементе од следећег нижег елемента.
Узмимо n-политоп са fi i-страним елементима (i = 0, ..., n). Његова (n + 1)-политопна призма ће имати 2fi + fi−1 i-страних елемената. (Са f−1 = 0, fn = 1.)
По димензији:
- Узмите многоугао са n врхова, n ивица. Његова призма има 2n темена, 3n ивица и 2 + n лица.
- Узмите полиедар са v врховима, e ивица и f површина. Његова призма има 2v темена, 2e + v ивице, 2f + e лица и 2 + f ћелије.
- Узмите полихорон са v врховима, e ивица, f површина и c ћелија. Његова призма има 2v темена, 2e + v ивице, 2f + e лица, 2c + f ћелија и 2 + c хиперћелије.
Уједначени призматични политоп[уреди | уреди извор]
Правилан n-политоп представљен Шлафлијевим симболом {p, q, ..., t} може формирати униформан призматични (n + 1)-политоп представљен картезијанским производом два Шлафлијева симбола: {p, q, ..., t}×{}.
По димензији:
- 0-политопна призма је сегмент линије, представљен празним Шлафлијевим симболом {}.
- 1-политопна призма је правоугаоник, направљен од 2 преведена сегмента. Представља се као производ Шафлијевог симбола {}×{}. Ако је квадратна, симетрија се може смањити: {}×{} = {4}.
- Полигонална призма је 3-димензионална призма направљена од два преведена полигона повезана правоугаоницима. Правилан многоугао {p} може да конструише униформну n-угаону призму представљену производом {p}×{}. Ако је p = 4, са квадратном симетријом, постаје коцка: {4}×{} = {4, 3}.
 Пример: Пентагонална призма, {5}×{}, два паралелна петоугла повезана са 5 правоугаоних страница.
Пример: Пентагонална призма, {5}×{}, два паралелна петоугла повезана са 5 правоугаоних страница.
- Полиедарска призма је 4-димензионална призма направљена од два преведена полиедра повезана ћелијама 3-димензионалне призме. Правилан полиедар {p, q} може конструисати униформну полихоријску призму, представљену производом {p, q}×{}. Ако је полиедар коцка, а странице коцке, он постаје тесеракт: {4, 3}×{} = {4, 3, 3}.
 Пример: Додекаедарска призма, {5, 3}×{}, два паралелна додекаедра повезана са 12 петоугаоних страница призме.
Пример: Додекаедарска призма, {5, 3}×{}, два паралелна додекаедра повезана са 12 петоугаоних страница призме.
Призматични политопи вишег реда такође постоје као картезијански производи било која два политопа. Димензија производа политопа је производ димензија његових елемената. Први примери ових постоје у 4-димензионалном простору; називају се дуопризми као производ два полигона. Регуларни дуопизми су представљени као {p}×{q}.
Галерија[уреди | уреди извор]
-
Права тространа призма
-
Коса неправила призма
Референце[уреди | уреди извор]
- ^ N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups, 11.3 Pyramids, Prisms, and Antiprisms, Figure 11.3b
- ^ Malton, Thomas (1774). A Royal Road to Geometry: Or, an Easy and Familiar Introduction to the Mathematics. ... By Thomas Malton. ... author, and sold. стр. 360—.
- ^ Elliot, James (1845). Key to the Complete Treatise on Practical Geometry and Mensuration: Containing Full Demonstrations of the Rules ... Longman, Brown, Green, and Longmans. стр. 3—.
- ^ William F. Kern, James R. Bland, Solid Mensuration with proofs, 1938, pp. 28
- ^ William F. Kern, James R. Bland, Solid Mensuration with proofs, 1938, pp. 81
- ^ Geometry handbookŽauthor=Catherine A. Gorini. The facts on file. 2003. стр. 172. ISBN 0-8160-4875-4.
Литература[уреди | уреди извор]
- Pugh, Anthony (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7.
- Љиљана Петрушевски - Полиедри
- Cromwell, P.;Polyhedra, CUP hbk (1997), pbk. (1999).
- Grünbaum, B. (1994). „Polyhedra with Hollow Faces”. Ур.: Tibor Bisztriczky; Peter McMullen; Rolf Schneider; et al. Proceedings of the NATO Advanced Study Institute on Polytopes: Abstract, Convex and Computational. Springer. стр. 43—70. ISBN 978-94-010-4398-4.
- Grünbaum, B.; Are your polyhedra the same as my polyhedra? Discrete and comput. geom: the Goodman-Pollack festschrift, ed. Aronov et al. Springer (2003) pp. 461–488. (pdf Архивирано на сајту Wayback Machine (3. август 2016))
- Bertrand, J. (1858). Note sur la théorie des polyèdres réguliers, Comptes rendus des séances de l'Académie des Sciences, 46, pp. 79–82.
- Haeckel, E. (1904). Kunstformen der Natur. Available as Haeckel, E. Art forms in nature, Prestel USA (1998), ISBN 3-7913-1990-6, or online at https://web.archive.org/web/20090627082453/http://caliban.mpiz-koeln.mpg.de/~stueber/haeckel/kunstformen/natur.html
- Smith, J. V. (1982). Geometrical And Structural Crystallography. John Wiley and Sons.
- Sommerville, D. M. Y. (1930). An Introduction to the Geometry of n Dimensions. E. P. Dutton, New York. (Dover Publications edition, 1958). Chapter X: The Regular Polytopes.
- Coxeter, H.S.M.; Regular Polytopes (third edition). Dover Publications Inc. ISBN 0-486-61480-8.
- Whitney, Hassler (1932). „Congruent graphs and the connectivity of graphs”. Amer. J. Math. 54 (1): 150—168. JSTOR 2371086. doi:10.2307/2371086. hdl:10338.dmlcz/101067.
- Blind, Roswitha; Mani-Levitska, Peter (1987), „Puzzles and polytope isomorphisms”, Aequationes Mathematicae, 34 (2–3): 287—297, MR 921106, doi:10.1007/BF01830678
- Kalai, Gil (1988), „A simple way to tell a simple polytope from its graph”, Journal of Combinatorial Theory, Ser. A, 49 (2): 381—383, MR 964396, doi:10.1016/0097-3165(88)90064-7
- Kaibel, Volker; Schwartz, Alexander (2003). „On the Complexity of Polytope Isomorphism Problems”. Graphs and Combinatorics. 19 (2): 215—230. arXiv:math/0106093
 . doi:10.1007/s00373-002-0503-y. Архивирано из оригинала 2015-07-21. г.
. doi:10.1007/s00373-002-0503-y. Архивирано из оригинала 2015-07-21. г. - Büeler, B.; Enge, A.; Fukuda, K. (2000). „Exact Volume Computation for Polytopes: A Practical Study”. Polytopes — Combinatorics and Computation. стр. 131. ISBN 978-3-7643-6351-2. doi:10.1007/978-3-0348-8438-9_6.
- Yao, Andrew Chi Chih (1981), „A lower bound to finding convex hulls”, Journal of the ACM, 28 (4): 780—787, MR 677089, doi:10.1145/322276.322289; Ben-Or, Michael (1983), „Lower Bounds for Algebraic Computation Trees”, Proceedings of the Fifteenth Annual ACM Symposium on Theory of Computing (STOC '83), стр. 80—86, doi:10.1145/800061.808735
- Cundy, H. Martyn; Rollett, A. P. (1961), Mathematical Models (2nd изд.), Oxford: Clarendon Press, MR 0124167.
- Gailiunas, P.; Sharp, J. (2005), „Duality of polyhedra”, International Journal of Mathematical Education in Science and Technology, 36 (6): 617—642, doi:10.1080/00207390500064049.
- Grünbaum, Branko (2003), „Are your polyhedra the same as my polyhedra?”, Ур.: Aronov, Boris; Basu, Saugata; Pach, János; Sharir, Micha, Discrete and Computational Geometry: The Goodman–Pollack Festschrift, Algorithms and Combinatorics, 25, Berlin: Springer, стр. 461—488, CiteSeerX 10.1.1.102.755
 , ISBN 978-3-642-62442-1, MR 2038487, doi:10.1007/978-3-642-55566-4_21.
, ISBN 978-3-642-62442-1, MR 2038487, doi:10.1007/978-3-642-55566-4_21. - Grünbaum, Branko (2007), „Graphs of polyhedra; polyhedra as graphs”, Discrete Mathematics, 307 (3–5): 445—463, MR 2287486, doi:10.1016/j.disc.2005.09.037.
- Grünbaum, Branko; Shephard, G. C. (2013), „Duality of polyhedra”, Ур.: Senechal, Marjorie, Shaping Space: Exploring polyhedra in nature, art, and the geometrical imagination, New York: Springer, стр. 211—216, ISBN 978-0-387-92713-8, MR 3077226, doi:10.1007/978-0-387-92714-5_15.
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 0-521-54325-8, MR 0730208.
- Barvinok, Alexander (2002), A course in convexity, Providence: American Mathematical Soc., ISBN 0821829688
Спољашње везе[уреди | уреди извор]
- Weisstein, Eric W. „Prism”. MathWorld.
- Paper models of prisms and antiprisms Free nets of prisms and antiprisms
- Paper models of prisms and antiprisms Using nets generated by Stella