Циклична група
У теорији група, циклична група или моногена група је група која може бити генерисана само од једног свог елемента, у смислу да је да група има елемент g („генератор“ групе) такав да, када се запише мултипликативно, сваки елемент групе је степен од g (умножак од g у случају адитивне нотације).
Дефиниција
[уреди | уреди извор]Група G се назива цикличном ако постоји елемент g у G, такав да G = <g> = { gn за сваки цео број n }. Како је свака група генерисана елементом групе подгрупа те групе, показивањем да је једина подгрупа групе G која садржи g сама G, показује се да је G циклична.
На пример, ако је G = { e, g1, g2, g3, g4, g5 }, онда је G циклична, и G је у суштини иста као (до на изоморфизам) група { 0, 1, 2, 3, 4, 5 } са сабирањем по модулу 6. То јест 1 + 2 mod 6 = 3, 2 + 5 mod 6 = 1, и тако даље. Може се користити изоморфизам φ дефинисан као φ(g) = 1.
За сваки позитиван цео број n постоји тачно једна циклична група (до на изоморфизам) чији ред је n, и постоји тачно једна бесконачна циклична група (цели бројеви у односу на сабирање). Стога су цикличне групе најједноставније групе.
Име 'циклична' може да доведе у забуну: могуће је генерисати бесконачно много елемената и не направити ниједан циклус; то јест, свако може бити различито. Група генерисана на овај начин је бесконачна циклична група, која је изоморфна адитивној групи целих бројева Z.
Групе се обично означавају адитивно на следећи начин: Z/n или Z/nZ. Мултипликативно, означавају се као Cn. (На пример, g3g4 = g2 у C5, где је 3 + 4 = 2 (mod 5) у Z/5.)
Све коначне цикличне групе су периодичне групе.
Својства
[уреди | уреди извор]Свака циклична група је изоморфна групи { 0, 1, 2, ..., n − 1 } у односу на сабирање по модулу n, или Z, адитивној групи свих целих бројева. Због тога су циклична групе најједноставније групе за изучавање и имају бројна згодна својства. Дата је циклична група G реда n (n може бити бесконачно). За свако g из G,
- G је Абелова група; то јест, операција групе је комутативна: gh = hg. Ово важи, јер је g + h mod n = h + g mod n.
- Ако је n бесконачно, тада јер n mod n = 0.
- Ако је n = ∞, тада постоје тачно два генератора: 1 и −1 за Z, а сви остали се пресликавају у њих под изоморфизмом у другим цикличним групама.
- Ако је n коначно, тада постоји тачно φ(n) генератора, где је φ() Ојлерова фи функција
- Свака подгрупа од G је циклична. Заиста, свака коначна подгрупа од G је група { 0, 1, 2, 3, ... m − 1} у односу на сабирање по модулу m. А свака бесконачна подгрупа од G је mZ' за неко m, које је бијективно (изоморфно) са Z'.
- Cn је изоморфно са Z/n, јер Z/n = {0 + nZ, 1 + nZ, 2 + nZ, 3 + nZ, 4 + nZ, ..., n − 1 + nZ} { 0, 1, 2, 3, 4, ..., n − 1} у односу на сабирање по модулу n.
Генератори 'Z'/n су класе остатака целих бројева који су узајамно прости са n; број тих генератора је познат као φ(n), где је φ Ојлерова фи функција.
Општије, ако d дели n, тада је број елемената у 'Z'/n, који су реда d једнак φ(d). Ред класе остатка од m је n / НЗД(n,m).
Ако је p прост број, тада је једина група (до на изоморфизам) са p елемената циклична група Cp или Z/p.
Директан производ две цикличне групе 'Z/n и 'Z/m је цикличан ако и само ако су n и m узајамно прости. Стога, на пример Z/12 је директан производ Z/3 и Z/4, али није директан производ Z/6 и Z/2.
Дефиниција имплицира да цикличне групе имају врло једноставну презентацију групе xn >.
Структурна теорема за коначне Абелове групе каже да је свака коначно генерисана Абелова група директан производ коначно много цикличних група.
'Z/n и Z су такође комутативни прстени. Ако је p прост, онда је 'Z/p коначно поље, што се такође означава са Fp или GF(p). Свако поље са p елемената је изоморфно овом пољу.
Јединице прстена 'Z'/n су бројеви узајамно прости са n. Они граде групу у односу на множење по модулу n са φ(n) елемената. То се записује као (Z/n)×. на пример, добијамо (Z/n)× = {1, 5} када је n = 6, и (Z/n)× = {1, 3, 5, 7} када је n = 8.
Познато је да је (Z/n)× циклична ако и само ако је n једнако 2 или 4 или pk или 2 pk за прост број већи од два p и k ≥ 1, у ком случају се сваки генератор Zn× назива примитивним кореном по модулу n. Стога, (Z/n)× је циклично за n = 6, али не за n = 8, када је изоморфно Клајновој четворној групи.
Група (Z/p)× је циклична са p − 1 елемената за свако просто p, што се записује и као (Z/p)* јер се састоји од не-нула елемената. Општије, свака коначна подгрупа мултипликативне групе било ког поља је циклична.
Примери
[уреди | уреди извор]У две и три димензије симетрија групе за n-пута ротациону симетрију је Cn, апстрактног типа групе Zn. У три димензије постоје и друге симетрије групе које су алгебарски исте.
Треба имати у виду да група S1 свих ротација круга (кружна група) није циклична, јер није ни пребројива.
nти Де Моавров број гради цикличну групу реда n у односу на множење, на пример, где је и група у односу на множење је циклична.
Представљање
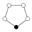
[уреди | уреди извор]Циклични графови коначних цикличних група су сви n-тострани полигони. Црна тачка у цикличном графу представља неутрал, а остали чворови су елементи групе. Цикл се састоји од узастопних степена било ког елемента повезаног са неутралом.
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 |