Sistem linearnih jednačina

Linearni sistem sa tri promenljive određuje skup ravni. Presek svih ravni je rešenje.

U matematici i linearnoj algebri, sistem linearnih jednačina je skup linearnih jednačina, kao što je

${\begin{array}{rcrcrcc}3x_{1}&+&2x_{2}&-&x_{3}&=&1\\2x_{1}&-&2x_{2}&+&4x_{3}&=&-2\\*x_{1}&+&{\frac {1}{2}}x_{2}&-&x_{3}&=&0\end{array}}$

Standardni problem je da se utvrdi da li postoji skup vrednosti za nepoznate $x_{1},x_{2},x_{3}\,\!$, koji zadovoljava sve jednačine istovremeno, i da se nađe takav skup ukoliko postoji. Postojanje skupa rešenja zavisi od jednačina, ali i od dostupnih vrednosti (da li se radi o celim brojevima, realnim brojevima, i slično). Sistem iz gornjeg primera ima jedinstveno rešenje:

${\begin{alignedat}{2}x_{1}&=&1\\x_{2}&=&-2\\x_{3}&=&-2\end{alignedat}}$

Istorija

Zadaci koji se svode na sastavljanje i rešavanje sistema jednačina sa dve ili više nepoznatih, bili su poznati još u vavilonskim i egipatskim tekstovima iz 2. milenijuma pre n.e., kao i u radovima starogrčkih, indijskih i kineskih matematičara.

Najpoznatija starokineska zbirka zadataka pod nazivom „Devet poglavlja veštine računanja.”, čiji je autor nepoznat, nastala je u vreme Han dinastije (iz period od 206. p. n. e. do 220. n.e), a njeno sedmo i osmo poglavlje se bave sistemima linearnih jednačina.

Jedan od zadatka iz najstarije kineske matematičke zbirke zadataka glasi: u kavezu se nalaze fazani i zečevi; sve te životinje imaju ukupno 35 glava i 94 noge. Treba naći broj fazana i broj zečeva. Rešenje zadatka glasi: ako bi u kavezu bili samo fazani, što je lažna pretpostavka, onda bi broj nogu iznosio 70, a ne 94. Prema tome, višak od 24 noge pripada zečevima – po dva svakome. Tada je jasno da je zečeva bilo 24 : 2 = 12, a fazana 35 - 12 = 23.

Karakteristično je da su u tim početnim zbirkama sistemi jednačina uvek bili sa jednakim brojem jednačina i nepoznatih. U sedmom poglavlju, koje nosi naziv „Višak – manjak” , izložena su dve metode za rešavanje zadataka, koji se svode na sistem dve linearne jednačine sa dve nepoznate. Poznavali su metodu determinanti, koja se danas naziva Kramerovim pravilom.

Jednačine su se rešavale šematski. Za njihovo rešavanje su data kratka pravila, pri čemu se sve izlaže rečima. Uputstva su bila formulisana tako da je svaki od koeficijenata uz nepoznate nosio svoj naziv, a postupak je razvijen polazeći od kineske table za računanja. Koeficijenti jednačine postavljeni su u vidu tablice, kao posebna vrsta abakusa. Pri ponovljenim operacijama na toj računaljci, jasno se vidi da sa koeficijentima treba postupati po istom pravilu, da bi se našlo rešenje sistema jednačina.

Drugi način koji su primenjivali je bila ono koja se danas naziva Gausova metoda eliminacije, a tada se zvala metoda dve lažne pretpostavke i primenjivana je naročito u srednjem veku, pa sve do 18. veka.

U 12. veku tehnika lažnih pretpostavki preneta je iz arapske u evropsku matematičku literaturu, gde je bila poznata pod latinskim nazivom lat. regula duorum falsorum – правило двеју грешака.

Sistem dve linearne jednačine sa dve nepoznate

Poseban slučaj sistema linearnih jednačina je skup od dve linearne jednačine sa dve nepoznate, odnosno promenljive, kod kojih su rešenja tih nepoznatih ista. Opšti oblik sistema dve jednačine sa dve nepoznate je sledeći:

${\begin{array}{rcrcccrcl}a_{1}\cdot x&+&b_{1}\cdot y&=&c_{1}\\a_{2}\cdot x&+&b_{2}\cdot y&=&c_{2}\\\end{array}}$

gde su x, y skup nepoznatih vrednosti, a koeficijenti $a_{1},a_{1},b_{1},b_{2},c_{1},c_{2}$ poznati parametri, u obliku realnih brojeva. Koeficijente $a_{1},a_{1},b_{1},b_{2}$ se nazivaju zadati koeficijenti, dok se koeficijenti $c_{1},c_{2}$ nazivaju slobodni koeficijenti. Rešenje ovog sistema bi bio svaki uređeni par brojeva $(x_{0},y_{0})\!$, za koji važi da je:

${\begin{array}{rcrcccrcl}a_{1}\cdot x_{0}&+&b_{1}\cdot y_{0}&=&c_{1}\\a_{2}\cdot x_{0}&+&b_{2}\cdot y_{0}&=&c_{2}\\\end{array}}$

Za sistem od dve linearne jednačine s dve nepoznate postoje tri mogućnosti:

• sistem je određen ako postoji samo jedno rešenje, odnosno jedan uređeni par $(x_{0},y_{0})\!$, koji zadovoljava sistem jednačina
• sistem je neodređen ako postoji beskonačno mnogo rešenja, odnosno uređenih parova $(x_{0},y_{0})\!$ koji zadovoljavaju sistem jednačina. Kada sistem sa dve jednačine i dve promeljnive ima više od jednog rešenja, onda je jedna promeneljiva slobodna.

Primer:

Sledeći sistem jednačina ima beskonačno mnogo rešenja:

${\begin{array}{rcrcccrcl}x+y=0\\2x+2y=0\\\end{array}}$

i ono se izražava u obliku $x=x_{0},y=x_{0}-1$ gde se za promenljivu x kaže da je slobodna, dok je promenljiva u vezana.

• sistem je nemoguć ili kontradiktoran, kada ne postoji nijedano rešenje za zadati sistem jednačina.

Primer:

Sledeći sistem jednačina je nemoguć, jer ne postoje brojevi koji bi mogli da je zadovolje:

${\begin{array}{rcrcccrcl}x+y=1\\x+y=2\\\end{array}}$

Ekvivalentnost sistema linearnih jednačina

Dva sistema jednačina su ekvivalentna ako je svako rešenje jednog od njih ujedno rešenje i drugog, ili ako oba sistema nemaju rešenje.

Sistem ekvivalentan sistemu, čija bar jedna jednačina nema rešenje, takođe nema rešenje.

U slučaju da zadati sistem nije predstavljen u opštem obliku, on se može svesti na opšti oblik ekvivalentnim transformacijama.

Transformacije koje sistem linearnih jednačina prevode u njemu ekvivalentan sistem su:

• zamena mesta dveju jednačina
• množenje svih koeficijenata jedne jednačine konstantom $c\neq 0$
• dodavanje koeficijenata jedne jednačine odgovarajućim koeficijentima druge jednačine

Ako jednačinu sistema zamenimo njoj ekvivalentnom, dobijamo novi sistem ekvivalentan polaznom. Ako u jednačini datog sistema zamenimo jednu od nepoznatih izrazom koji je jednak toj nepoznatoj na osnovu druge jednačine, dobijamo novi sistem koji je ekvivalentan polaznom sistemu. Ako jednu jednačinu datog sistema zamenimo jednačinom koja je zbir ili razlika jednačina datog sistema, dobijamo novi sistem koji je ekvivalentan polaznom sistemu.

Primer: Ako se u polaznom sistemu jednačina

${\begin{array}{rcrcccrcl}x-y=0\\x+y=2\\\end{array}}$

druga jednačina zameni zbirom prve i druge jednačine:

${\begin{array}{rcrcccrcl}x-y=0\\x-y+x+y=2\\\end{array}}$

i promenljiva y izrazi preko promenljive x u prvoj jednačini, a druga jednačina podeli sa 2:

${\begin{array}{rcrcccrcl}y=x\\2\cdot x=2&/&:2\\\end{array}}$

te dobijena vrednost za x iz druge jednačine zameni u prvoj jednačini, dobijeni sistem jednačina je ekvivalentan početnom sistemu:

${\begin{array}{rcrcccrcl}y=1\\x=1\\\end{array}}$

Radi preglednosti i lakšeg rešavanja iste nepoznate se obično pišu jedna ispod druge.

Metode rešavanja sistema dve linearne jednačine

Rešiti sistem jednačina znači odrediti rešenje ili rešenja tog sistema ili utvrditi da taj sistem nema rešenje. Pod rešavanjem sistema linearnih jednačina s dve nepoznate podrazumeva se niz postu- paka kojim se ekvivalentnim transformacijama sistem prevodi u sistem čije se rešenje neposredno određuje. Postoji više metoda za rešavanja sistema linearnih jednačina i sve one dovode do istog rešenja, a za rešavanje se bira ona metoda koja se čini najpogodnija za postavljeni sistem, odnosno da se dobije ekvivalentan sistem u najjednostavnijem obliku.

Metoda zamene

Glavni članak: Metod zamene

Postupak se sastoji u tome da se na osnovu jedne od dve zadate jednačine jedna nepoznata izrazi preko druge nepoznate (x preko y ili y preko x), a zatim se tako izražena nepoznata zameni u drugoj jednačini, čime se problem svodi na rešavanje jedne jednačine sa jednom nepoznatom. Izbor o tome koju promenljivu izraziti preko druge je slobodan, tako da se bira ono što je u datom slučaju pogodnije.

Metodu zamene je nabolje primenjivati kada je bar jedan koeficijent uz neku od nepoznatih jednak 1 ili -1, jer se tada primenom pravila o dodavanju jedna nepoznata lako izražava preko druge.

Primer 1:

${\begin{array}{rcrcccrcl}x&+&7\cdot y&=&28\\2\cdot x&-&y&=&11\\\end{array}}$

Rešavanje:

Nepoznata x se u prvoj jednačini izrazi preko nepoznate y:

${\begin{array}{rcrcccrcl}x&=&28&-&7\cdot y\end{array}}$

i zameni u drugoj jednačini:

${\begin{array}{rcrcccrcl}2\cdot (28&-&7\cdot y)&-&y&=&11\end{array}}$

odnosno, množenjem cele jednačine sa -1:

${\begin{array}{rcrcccrcl}56&-&14\cdot y&-&y&=&11&/\cdot (-1)\end{array}}$

${\begin{array}{rcrcccrcl}15\cdot y&=&56&-&11\end{array}}$

što se svodi na:

${\begin{array}{rcrcccrcl}y&=&45&:&15\end{array}}$

${\begin{array}{rcrcccrcl}y&=&3\end{array}}$

Zamenom vrednosti za $y\!$ , u jednačini u kojoj je x izraženo preko y dobija se :

${\begin{array}{rcrcccrcl}x&=&28&-&7\cdot 3\end{array}}$

${\begin{array}{rcrcccrcl}x=7\end{array}}$

Zaključujemo da je postavljeni sistem jednačina određen i da njegovo rešenje predstavlja uređeni par s vrednostima $(x_{0}=7,y_{0}=3)$.

Provera:

Provera tačnosti rešenja se vrši zamenom izračunatog rešenja, odnosno uređenog para izračunatih vrednosti u početne jednačine:

${\begin{array}{rcrcccrcl}7&+&7\cdot 3&=&28\\2\cdot 7&-&3&=&11\\\end{array}}$

Primer 2:

${\begin{array}{rcrcccrcl}2\cdot x&-&y&=&4\\*2\cdot x&+&y&=&6\\\end{array}}$

Rešavanje: Nepoznata y se u prvoj jednačini izrazi preko nepoznate x:

${\begin{array}{rcrcccrcl}y&=&2\cdot x&+&4\end{array}}$

i zameni u drugoj jednačini:

${\begin{array}{rcrcccrcl}-2\cdot x&+&2\cdot x&+&4&=&6\end{array}}$

što se svodi na:

${\begin{array}{rcrcccrcl}4&=&6\end{array}}$

i znači da je sistem jednačina nemoguć, odnosno da nema rešenja.

Metoda suprotnih koeficijenata

Za metodu suprotnih koeficijenata ključna je primena pravila koje glasi: ako jednu od jednačina sistema zamenimo zbirom ili razlikom jednačina tog sistema, dobijamo sistem ekvivalentan polaznom sistemu. Postupak se sastoji u množenju jednačine odgovarajućim brojem, pri čemu se koeficijenti ispred jedne od nepoznatih u obe jednačine pretvaraju u iste brojeve.

Ako su znaci ispred te nepoznate suprotni, sabiranjem jednačina se ta nepoznata eliminiše, a ako su znaci isti, da bi se jedna nepoznata eliminisala, jednačine se oduzimaju. Elminisanjem jedne od nepoznatih, problem se ponovo svodi na jednu jednačinu sa jednom nepoznatom. Eliminisana nepoznata se kasnije može izračunati zamenom prve izračunate nepoznate u bilo kojoj od postavljenih jednačina.

Metodu suprotnih koeficijenata je najzgodnije primenjivati kada su koeficijenti uz istu nepoznatu u obe jednačine sistema međusobno suprotni brojevi ili međusobno jednaki brojevi.

Primer 1:

${\begin{array}{rcrcccrcl}x&+&7\cdot y&=&28\\2\cdot x&-&y&=&11\\\end{array}}$

Rešavanje:

Da bi se dobili suprotni koeficijenti, najlakše je pomnožiti prvu jednačinu sa -2:

${\begin{array}{rcrcccrcl}&&x&+&7\cdot y&=&28&/\cdot (-2)\end{array}}$

${\begin{array}{rcrcccrcl}-2\cdot x&-&14\cdot y&=&-56\end{array}}$

Sabiranjem jednačina dobijamo:

${\begin{array}{rcrcccrcl}-2\cdot x&-&14\cdot y&+&2\cdot x&-&y&&=&-56&+&11\end{array}}$

množenjem sa -1:

${\begin{array}{rcrcccrcl}-15\cdot y=-45&/\cdot (-1)\end{array}}$

se svodi na:

${\begin{array}{rcrcccrcl}y&=&45&:&15\end{array}}$

${\begin{array}{rcrcccrcl}y&=&3\end{array}}$

Da bi se dobila vrednost za x, dovoljno je zameniti vrednost za y, u bilo kojoj od dve jednačine. Na primer, zamenom u prvoj jednačini:

${\begin{array}{rcrcccrcl}x&+&7\cdot 3&=&28\end{array}}$

${\begin{array}{rcrcccrcl}x&=&28&-&21\end{array}}$

${\begin{array}{rcrcccrcl}x&=&7\end{array}}$

Zaključujemo da je postavljeni sistem jednačina određen i da njegovo rešenje predstavlja uređeni par s vrednostima $(x_{0}=7,y_{0}=3)$.

Grafička metoda

Postupak se sastoji u grafičkom predstavljanju svake od zadatih jednačina. S obzirom da su nepoznate linearno zavisne, njihova grafička predstava je linearna funkcija, koja ima oblik prave linije u istoj ravni, a za konstruisanje prava dovoljno je izračunati vrednosti nepoznatih (x, y) u samo dve tačke, kao na primer, u tačkama x = 0 i y = 0. Grafičko rešavanje sistema se sastoji u traženju na grafiku uređenog para $(x_{0},y_{0})\!$, u kome se prave seku.

Dve prave jedne ravni mogu se naći u jednom od tri različita međusobna odnosa:

• prave se seku, odnosno imaju samo jednu zajedničku tačku. U tom slučaju sistem je određen i postoji jedinstveno rešenje
• prave su paralelne, ali se ne poklapaju, rastojanje između njih je uvek isto i nemaju zajedničkih tačaka. U tom slučaju se radi o nemogućem sistemu, odnosno rešenje za postavljeni sistem ne postoji
• prave se poklapaju, odnosno imaju beskonačno mnogo zajedničkih tačaka. To znači da sistem jednačina ima beskonačno mnogo rešenja i da je sistem neodređen

Primer 1:

${\begin{array}{rcrcccrcl}x&+&7\cdot y&=&28\\2\cdot x&-&y&=&11\\\end{array}}$

Rešavanje:

U prvoj jednačini se y izražava preko x na sledeći način:

${\begin{array}{rcrcccrcl}7\cdot y&=&28&-&x\end{array}}$

${\begin{array}{rcrcccrcl}y&=&(28&-&x)&:&7\end{array}}$

Da bi se nacrtala funkcija, može se koristiti tabela, na primer za vrednosti x = 0 i x = 7:

x	0	7
y	4	3

U drugoj jednačini se y izražava preko x na sledeći način:

${\begin{array}{rcrcccrcl}-y&=&11&-&2\cdot x\end{array}}$

Množenjem sa -1 dobija se:

${\begin{array}{rcrcccrcl}-y&=&11&-&2\cdot x&/\cdot (-1)\end{array}}$

${\begin{array}{rcrcccrcl}y&=&-11&+&2\cdot x\end{array}}$

${\begin{array}{rcrcccrcl}y&=&2\cdot x&-&11\end{array}}$

Da bi se nacrtala funkcija može se koristiti tabela za vrednosti x = 0 i x = 5:

x	0	5
y	-11	-1

Rešenje jednačina se dobija u preseku pravih, koja se nalazi u tačci (7,3), odnosno sistem ima jedinstveno rešenje:

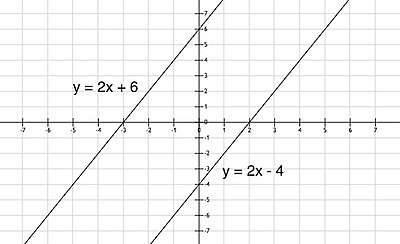
Primer 2:

${\begin{array}{rcrcccrcl}2\cdot x&-&y&=&4\\*2\cdot x&+&y&=&6\\\end{array}}$

Rešavanje:

Iz prve jednačine se izrazi y preko x:

${\begin{array}{rcrcccrcl}y&=&2\cdot x&-&4\end{array}}$

Zatim se izračunaju vrednosti y za najmanje dve vrednosti x zašta se može koristiti tabela:

x	0	2
y	-4	0

Iz druge jednačine se izrazi y preko x:

${\begin{array}{rcrcccrcl}y&=&2\cdot x&+&6\end{array}}$

Zatim se izračunaju vrednosti y za najmanje dve vrednosti x zašta se može koristiti tabela:

x	0	-3
y	6	0

Crtanjem funkcija vidimo da su prave paralelne, nema preseka, zadati sistem jednačina nema rešenje

Primer 3:

${\begin{array}{rcrcccrcl}x&-&y&=&4\\4\cdot x&-&4\cdot y&=&16\\\end{array}}$

Rešavanje:

Poređenjem jednačina može se uočiti da su jednačine ekvivalente, odnosno da se druga jednačina dobija množenjem prve jednačine sa 4, odnosno obe jednačine se mogu predstaviti istom funkcijom:

${\begin{array}{rcrcccrcl}y&=&x&-&4\end{array}}$

Da bi se nacrtala funkcija potrebno pronaći najmanje dve tačke, zašta koristimo tabelu:

x	0	4
y	-4	0

Primena sistema dve linearne jednačine sa dve nepoznate

Sistemi linearnih jednačina se javljaju pri rešavanju različitih problema. Primeri:

Primer 1:

Zbir dva broja je za 2 veći od trostruke vrednosti manjeg od ta dva broja, a petostruka vrednost manjeg je jednaka dvostrukoj vrednosti većeg. O kojim brojevima je reč?

Postavka sistema jednačina:

Neka je x manji od dva tražena broja, a y veći. U tom slučaju može se postaviti sledeći sistem jednačina:

${\begin{array}{rcrcccrcl}x&+&y&=&3\cdot x+2\\5\cdot x&=&2\cdot y\\\end{array}}$

Rešavanje:

Metodom zamene može se izraziti vrednost promenljive y preko promenljive x:

${\begin{array}{rcrcccrcl}y&=&3\cdot x&-&x&+&2\end{array}}$

${\begin{array}{rcrcccrcl}y&=&2\cdot x&+&2\end{array}}$

kada se ova vrednost zameni u drugoj jednačini dobija se:

${\begin{array}{rcrcccrcl}5\cdot x&=&2\cdot &(&2\cdot x&+&2&)&\end{array}}$

${\begin{array}{rcrcccrcl}5\cdot x&=&4\cdot x&+&4\end{array}}$

${\begin{array}{rcrcccrcl}x&=&4\end{array}}$

Zamenom dobijene vrednosti za x u ekvivalentnoj jednačini:

${\begin{array}{rcrcccrcl}y&=&2\cdot x&+&2\end{array}}$

dobija se:

${\begin{array}{rcrcccrcl}y&=&2&\cdot &4&+&2\end{array}}$

${\begin{array}{rcrcccrcl}y&=&10\end{array}}$

Traženi brojevi su 4 i 10.

Provera:

Zamenom dobijenih vrednosti za x i y, u prvoj i drugoj jednačini se dobija:

${\begin{array}{rcrcccrcl}4&+&10&=&3\cdot 4+2\\5\cdot 4&=&2\cdot 10\\\end{array}}$

Oba izraza su tačna.

Primer 2: Duž istog puta ravnomernom brzinom u istom smeru se kreću kamion i iza njega automobil. U početku rastojanje između ova dva vozila je iznosilo 400 m. Nakon 40 sekundi automobil je stigao kamion. Tada je kamion smanjio svoju brzinu za trećinu i nakon 20 sekundi rastojanje između vozila je iznosilo 300 m, pri čemu je automobil bio ispred kamiona. Odrediti prvobitne brzine kojim su se kretali automobil i kamion.

Postavka sistema jednačina:

Neka je $v_{1}\!$ prvobitna brzina kamiona (izražena u ${\frac {m}{s}}\!$), a $v_{2}\!$ prvobitna brzina automobila (takođe izražena u ${\frac {m}{s}}\!$). U tom slučaju mogu se postaviti jednačine pređenih puteva, kamiona i automobila, nakon prvih 30 sekundi i nakon narednih 20 sekundi:

${\begin{array}{rcrcccrcl}40\cdot v_{1}&+&400&=&40\cdot v_{2}\\20\cdot {\frac {2}{3}}\cdot v_{1}&+&300&=&20\cdot v_{2}\\\end{array}}$

Rešavanje: Deljenjem prve jednačine sa 40 i druge jednačine sa 20 sistem se svodi na:

${\begin{array}{rcrcccrcl}v_{1}&+&10&=&v_{2}\\{\frac {2}{3}}\cdot v_{1}&+&15&=&v_{2}\\\end{array}}$

Koji se najlakše rešava primenom negativnih koeficijenta, odnosno oduzimanje druge jednačine od prve:

${\begin{array}{rcrcccrcl}v_{1}&+&10-{\frac {2}{3}}\cdot v_{1}&-&15&=&v_{2}-v_{2}\end{array}}$

odnosno

${\begin{array}{rcrcccrcl}{\frac {1}{3}}\cdot v_{1}&=&5\end{array}}$

odakle se dobija:

${\begin{array}{rcrcccrcl}v_{1}&=&5\cdot 3\end{array}}$

${\begin{array}{rcrcccrcl}v_{1}&=&15\end{array}}$

Zamenom vrednosti $v_{1}\!$ u prvoj jednačini dobija se:

${\begin{array}{rcrcccrcl}15&+&10&=&v_{2}\end{array}}$

odnosno:

${\begin{array}{rcrcccrcl}v_{2}&=&25\end{array}}$

Brzina kamiona $v_{1}\!$ iznosila je na početku 15 ${\frac {m}{s}}\!$, a automobila 25 ${\frac {m}{s}}\!$.

Gausova metoda eliminacije

U sistemu od dve linearnih jednačine sa dve nepoznate:

${\begin{array}{rcrcccrcl}a_{1}\cdot x+b_{1}\cdot y&=&c_{1}\\a_{2}\cdot x+b_{2}\cdot y&=&c_{2}\\\end{array}}$

Ako pretpostavimo da je $a_{1}\neq 0$ prva jednačina se može pomnožiti sa brojem $-{\frac {a_{2}}{a_{1}}}$:

$a_{1}\cdot x+b_{1}\cdot y=c_{1}/\cdot -{\frac {a_{2}}{a_{1}}}$

$-a_{2}\cdot x-{\frac {a_{2}}{a_{1}}}\cdot b_{1}\cdot y=-c_{1}\cdot {\frac {a_{2}}{a_{1}}}$

i sabere se sa drugom jednačinom dobija se:

$b_{2}\cdot y-{\frac {a_{2}}{a_{1}}}\cdot b_{1}\cdot y=c_{2}-c_{1}\cdot {\frac {a_{2}}{a_{1}}}$

odnosno:

${\frac {(a_{1}\cdot b_{2}-a_{2}\cdot b_{1})}{a_{1}}}\cdot y={\frac {a_{1}\cdot c_{2}-c_{1}\cdot {a_{2}}}{a_{1}}}$

Dobija se sistem u kome treba posmatrati nekoliko slučajeva slučajeva.

Ako je razlika $a_{1}\cdot b_{2}-a_{2}\cdot b_{1}\neq 0$, odnosno ${\frac {a_{1}}{a_{2}}}\neq {\frac {b_{1}}{b_{2}}}$ sistem ima jedinstveno rešenje $(x_{0},y_{0})$ koje je određeno formulama:

$x_{0}={\frac {c_{1}\cdot b_{2}-c_{2}\cdot b_{1}}{a_{1}\cdot b_{2}-a_{2}\cdot b_{1}}}$ , $y_{0}={\frac {a_{1}\cdot c_{2}-a_{2}\cdot c_{1}}{a_{1}\cdot b_{2}-a_{2}\cdot b_{1}}}$

Ako je razlika $a_{1}\cdot b_{2}-a_{2}\cdot b_{1}=0$ i bar jedan od brojeva $c_{1}\cdot b_{2}-c_{2}\cdot b_{1}$ ili $a_{1}\cdot c_{2}-a_{2}\cdot c_{1}$ različit od nule, odnosno ${\frac {a_{1}}{a_{2}}}={\frac {b_{1}}{b_{2}}}\neq {\frac {c_{1}}{c_{2}}}$ sistem nema rešenja.

Ako je razlika $a_{1}\cdot b_{2}-a_{2}\cdot b_{1}=c_{1}\cdot b_{2}-c_{2}\cdot b_{1}=0$ razlikuju se tri slučaja:

• Ako je bar jedan od brojeva $a_{1},b_{1},a_{2},b_{2}$ različit od 0, sistem ima beskonačno mnogo rešenja, odnosno neodređen je. Tako, na primer, ako je $a_{1}\neq 0$ rešenje su svi parovi realinih brojeva za koje važi $({\frac {c_{1}-b_{1}\cdot y}{a_{1}}},y)$, gde $y\in \mathbb {R}$.
• ako je $a_{1}=b_{1}=a_{2}=b_{2}=0$ i bar jedan od brojeva $c_{1},c_{2}$ različit od nule, sistem nema rešenje.
• ako je $a_{1}=b_{1}=c_{1}=a_{2}=b_{2}=c_{2}=0$ sistem je neodređen, ima beskonačno mnogo rešenja, svaki par $(x,y),x,y\in \mathbb {R}$ je rešenje sistema.

Opšti oblik sistema linearnih jednačina

Uopšteno, sistem sa m linearnih jednačina i n nepoznatih se zapisuje na sledeći način

${\begin{array}{rcrcccrcl}a_{11}x_{1}&+&a_{12}x_{2}&+&\cdots &+&a_{1n}x_{n}&=&b_{1}\\a_{21}x_{1}&+&a_{22}x_{2}&+&\cdots &+&a_{2n}x_{n}&=&b_{2}\\&&&\vdots &&&&&\vdots \\a_{m1}x_{1}&+&a_{m2}x_{2}&+&\cdots &+&a_{mn}x_{n}&=&b_{m}\end{array}}$

gde su $x_{1},\ x_{2},...,x_{n}$ nepoznate, a brojevi $a_{11},\ a_{12},...,\ a_{mn}$ su koeficijenti sistema.

Pod rešenjem sistema linearnih jednačina podrazumevamo bilo koji skup od n brojeva $\alpha _{1},\alpha _{2},\alpha _{3},...,\alpha _{n}$, koji za $x_{1}=\alpha _{1},x_{1}=\alpha _{2},x_{3}=\alpha _{3},...,x_{n}=\alpha _{n}$ identički zadovoljavaju sistem.

Stavljamo koeficijente u matricu na sledeći način:

${\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\end{bmatrix}}{\begin{bmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{bmatrix}}={\begin{bmatrix}b_{1}\\b_{2}\\\vdots \\b_{m}\end{bmatrix}}$

Ako predstavimo svaku matricu slovom, ovo postaje

$A\mathbf {x} =\mathbf {b}$

gde je A a m×n matrica, x je vektor kolona sa n članova, a b je vektor kolona sa m članova. Gaus-Žordanova eliminacija se primenjuje na sve ove sisteme, čak i ako su koeficijenti iz nekog proizvoljnog polja.

Ako je polje beskonačno (kao u slučaju realnih ili kompleksnih brojeva), moguća su samo sledeća tri slučaja (tačno jedan će biti tačan) za svaki dati sistem linearnih jednačina:

• sistem nema rešenja (sistem je protivrečan)
• sistem ima tačno jedno rešenje
• sistem ima beskonačno mnogo rešenja

Određen i neodređen sistemi imaju zajednički naziv, saglasni sistemi. Saglasni sistem ima najmanje jedno rešenje.

Ako su svi slobodni članovi $b_{1}=b_{2}=b_{3}=...=b_{m}=0$ sistem oblika

$A\mathbf {x} =\mathbf {0}$

se naziva homogenim sistemom linearnih jednačina. Svaki homogen sistem je saglasan, jer ima bar jedno rešenje $x_{1}=x_{2}=...=x_{n}=0$. Ovakvo rešenje se naziva trivijalno rešenje. Ako je homogen sistem sistem određen, onda on ima samo trivijalno rešenje. Neodređeni homogeni sistem ima i netrivijalno rešenje.

Skup svih rešenja sistema se naziva nula prostorom matrice A. Posebno u svetlu obilja gore navedenih primena, nekoliko efikasnijih alternativa Gaus-Žordanovoj eliminaciji je razvijeno za širok spektar specijalnih slučajeva. Mnogi od ovih poboljšanih algoritama su složenosti O(n²) (vidi: notacija velikog O). Neki od najuobičajenijih specijalnih slučajeva su:

• Za probleme oblika Ax' = b', gde je A simetrična Teplicova matrica, može se koristiti Levinsonova rekurzija ili neka od njenih varijacija. Jedna od često okrišćenih varijacija je Šurova rekurzija, koja se koristi u obradi digitalnih signala.
• Za probleme oblika Ax' = b', gde je A singularna matrica, ili gotovo singularna, matrica A se dekomponuje u proizvod tri matrica. Matrice sa leve i desne strane su levi i desni singularni vektori. Matrica u sredini je dijagonalna matrica i sadrži singularne vrednosti. Matrica tada može biti invertovanja prostom zamenom redosleda tri komponente, transponovanjem matrica singularnih vektora, i uzimanjem recipročne vrednosti dijagonalnih elemenata središnje matrice. Ako je bilo koja od singularnih vrednosti suviše blizu nule, i stoga blizu singularnosti, postavlja se na nulu.

Primena sistema linearnih jednačina

Sistemi linearnih jednačina spadaju među najstarije matematičke probleme, i imaju mnoge primene, kao što su obrada digitalnih signala, procene, predviđanje, kao i linearno programiranje, i aproksimacija nelinearnih problema u numeričkoj analizi. Postoji mnogo načina da se reši sistem linearnih jednačina. Međutim, među najefikasnijima su Gausov postupak i dekompozicija Čoleskog.

Literatura

• Ayres, Frank, Schaum's Outline of Modern Abstract Algebra, McGraw-Hill; 1st edition (June 1). 1965. ISBN 978-0-07-002655-1..
• Branković, Biljana (2015). Sistemi jednačina u školi sa osvrtom na problemske zadatke master rad (PDF). Beograd: Matematički fakultet Univerzitet u Beogradu. Pristupljeno 20. 5. 2018. 

Vidi još

• Gaus-Zajdelova metoda
• Kramerovo pravilo
• Metod zamene

Spoljašnje veze

• Onlajn linearni rešavač
• Sistem linearnih jednačina sa kalkulatorom
• Sistemi linearnih diferencijalnih jednačina
• (jezik: francuski) Rešenje linearnih sistema Arhivirano na sajtu Wayback Machine (15. septembar 2007)