Радијан
| Радијан | |
|---|---|
| Систем | Изведене јединице СИ система |
| Јединица | Угао |
| Симбол | rad или c |
| У јединицама | Без димензија са дужином лука једнаком полупречнику, тј. 1 m/m |
| Јединична претварања | |
| 1 rad у ... | ... је једнак са ... |
| милирадијани | 1000 mrad |
| обрт | 1/2π обрт |
| степена | 180/π ≈ 57,296° |
| града | 200/π ≈ 63,662g |
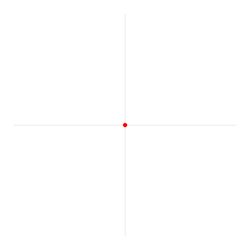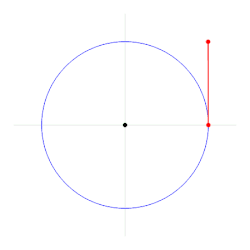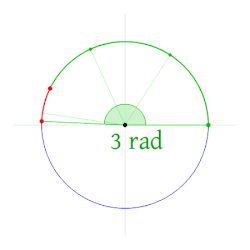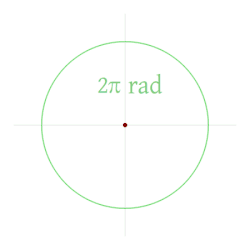
У математици и физици, радијан је мерна јединица угла. То је СИ изведена јединица за угао.[1] Дефинисана је као угао код центра круга затворен луком кружнице који је једнак у дужини полупречнику круга. Мере угла у радијанима су често дате без икакве експлицитне јединице. Када се да јединица, користи се скраћеница rad, а понекад симбол c (за циркуларни).
Дефиниција[уреди | уреди извор]

Један радијан се дефинише као угао формиран од центра круга који пресеца лук једнаке дужине полупречнику круга.[2] Уопштеније, магнитуда тог угла у радијанима једнака је односу дужине лука и полупречника круга; то јест, θ = s/r, где је θ угао у радијанима, s је дужина лука, а r је полупречник. Супротно томе, дужина пресеченог лука једнака је полупречнику помноженом са величином угла у радијанима; односно s = rθ.
Као однос две дужине, радијан је чист број.[а] У СИ, радијан је дефинисан као да има вредност 1.[6] Као последица тога, у математичком писању, симбол „rad“ се скоро увек изоставља. Када се квантификује угао у одсуству било ког симбола, претпостављају се радијани, а када се мисли на степене, користи се знак степена °.
Из тога следи да је величина у радијанима једног потпуног обртаја (360 степени) дужина целог обима подељена полупречником, или 2πr / r, или 2π. Тако је 2π радијана једнако 360 степени, што значи да је један радијан једнак 180/π ≈ 57,295779513082320876 степени.[7]
Релација 2π rad = 360° се може извести коришћењем формуле за дужину лука, , и коришћењем круга полупречника 1. Пошто је радијан мера угла који спаја лук дужине једнаке полупречнику круга, следи . Ово се даље може поједноставити на . Множење обе стране са 360° даје 360° = 2π rad.
Историја[уреди | уреди извор]
Концепт радијанске мере, за разлику од степена угла, обично се приписује Роџеру Котсу 1714. године.[8][9] Он је описао радијан у свему осим у имену и препознао његову природност као јединицу угаоне мере. Пре него што је термин радијан постао широко распрострањен, јединица се обично звала кружна мера угла.[10]
Идеју о мерењу углова дужином лука већ су користили други математичари. На пример, ал-Каши (око 1400) користио је такозване делове пречника као јединице, где је један део пречника био 1/60 радијана. Такође су користили сексагезималне подјединице дела пречника.[11]
Термин радијан се први пут појавио у штампи 5. јуна 1873. у испитним питањима које је поставио Џејмс Томсон (брат лорда Келвина) на Квинс колеџу у Белфасту. Он је користио тај термин још 1871. године, док је 1869. Томас Мјур, тада са Универзитета Сент Ендруз, колебао између појмова rad, radial, и radian. Године 1874, након консултација са Џејмсом Томсоном, Мјур је усвојио радијан.[12][13][14] Име радијан није било универзално усвојено неко време након овога. Лонгмансова школска тригонометрија је и користила назив радијанска кружна мера када је објављена 1890.[15]
Симбол јединице[уреди | уреди извор]
Међународни биро за тегове и мере[16] и Међународна организација за стандардизацију[17] наводе rad као симбол радијана. Алтернативни симболи који су коришћени пре 100 година су c (наднасловно написано слово c, за „кружну меру“), слово r или суперскрипт R,[18] али се ове варијанте ретко користе, јер могу бити помешане са симболом степена (°) или полупречником (r). Стога би вредност од 1,2 радијана најчешће била записана као 1,2 rad; друге ознаке укључују 1,2 r, 1,2rad, 1,2c, или 1,2R.
Конверзије[уреди | уреди извор]
Постоје 2π (око 6,283185) радијана у пуном кругу, па:
2π rad = 360°
1 rad = 360°/2π = 180°/π (приближно 57,29578°).
или:
У математичкој анализи, углови морају да се представе у радијанима у тригонометријским функцијама, да би идентитети и резултати били што простији и природнији. На пример, употреба радијана води до простог идентитета
- ,
који је основа за многе друге елегантне идентитете у математици, укључујући
- .
Радијан је пре био СИ допунска јединица, али је ова категорија укинута из СИ система 1995. године.
Треба нагласити да, иако је радијан јединица за меру, све мерено у радијанима је бездимензионално. Ово може лако да се уочи у томе да је однос дужине лука и полупречника у ствари угао лука, мерен у радијанима; а ипак количник два растојања је без димензија. Величине углова су напросто бројеви—у математичком смислу—а не физичке величине мерене у односу на известан фиксан еталон. Величина угла, у радијанима, степенима или ма којој другој јединици, независна је од јединице која се користи за изражавање дужина и других физичких мерљивих величина.
За мерење просторних углова, видите стерадијан.
Предности мерења у радијанима[уреди | уреди извор]

У калкулусу и већини других грана математике изван практичне геометрије, углови се универзално мере у радијанима. То је зато што радијани имају математичку „природности” која доводи до елегантније формулације бројних важних резултата. Што је најважније, резултати у анализи која укључује тригонометријске функције могу се елегантно навести, када су аргументи функција изражени у радијанима. На пример, употреба радијана доводи до једноставне формуле лимита
што је основа многих других идентитета у математици, укључујући
Због ових и других својстава, тригонометријске функције се појављују у решењима математичких проблема који нису очигледно повезани са геометријским значењима функција (на пример, решења диференцијалне једначине: , израчунавања интеграла и тако даље). У свим таквим случајевима, нађено је да су аргументи функција најприродније написани у облику који одговара, у геометријском контексту, радијанском мерењу углова.
Тригонометријске функције такође имају једноставна и елегантна проширења серије када се користе радијани. На пример, када је x у радијанима, Тејлоров низ за sin x постаје:
Ако је x изражено у степенима, онда би серија садржала непрегледне факторе који укључују степене π/180: ако је x број степени, број радијана је y = πx / 180, тако да
У сличном духу, математички важни односи између синусних и косинусних функција и експоненцијалне функције (погледајте, на пример, Ојлерову формулу) могу се елегантно изразити, када су аргументи функција у радијанима (а иначе неуредни).
Димензионална анализа[уреди | уреди извор]
Иако је радијан јединица мере, он је бездимензионална величина. Ово се може видети из раније дате дефиниције: угао везан за центар круга, мерен у радијанима, једнак је односу дужине затвореног лука и дужине полупречника круга. Пошто се мерне јединице поништавају, овај однос је бездимензионалан.
Иако поларне и сферне координате користе радијане за описивање координата у две и три димензије, јединица се изводи из радијусне координате, тако да је мера угла и даље бездимензионална.[19]
Види још[уреди | уреди извор]
Напомене[уреди | уреди извор]
Референце[уреди | уреди извор]
- ^ „Resolution 8 of the CGPM at its 20th Meeting (1995)”. Bureau International des Poids et Mesures. Архивирано из оригинала 2018-12-25. г. Приступљено 2014-09-23.
- ^ Protter, Murray H.; Morrey, Charles B., Jr. (1970), College Calculus with Analytic Geometry (2nd изд.), Reading: Addison-Wesley, стр. APP-4, LCCN 76087042
- ^ Mohr, J. C.; Phillips, W. D. (2015). „Dimensionless Units in the SI”. Metrologia. 52 (1): 40—47. Bibcode:2015Metro..52...40M. S2CID 3328342. arXiv:1409.2794
 . doi:10.1088/0026-1394/52/1/40.
. doi:10.1088/0026-1394/52/1/40.
- ^ Mills, I. M. (2016). „On the units radian and cycle for the quantity plane angle”. Metrologia. 53 (3): 991—997. Bibcode:2016Metro..53..991M. doi:10.1088/0026-1394/53/3/991.
- ^ „SI units need reform to avoid confusion”. Editorial. Nature. 548 (7666): 135. 7. 8. 2011. PMID 28796224. doi:10.1038/548135b
 .
.
- ^ ISO 80000-3:2006
- ^ а б Weisstein, Eric W. „Radian”. mathworld.wolfram.com (на језику: енглески). Приступљено 2020-08-31.
- ^ O'Connor, J. J.; Robertson, E. F. (фебруар 2005). „Biography of Roger Cotes”. The MacTutor History of Mathematics. Архивирано из оригинала 2012-09-24. г. Приступљено 2006-04-21.
- ^ Roger Cotes died in 1716. By 1722, his cousin Robert Smith had collected and published Cotes' mathematical writings in a book, Harmonia mensurarum … . In a chapter of editorial comments by Smith, he gives, for the first time, the value of one radian in degrees. See: Roger Cotes with Robert Smith, ed., Harmonia mensurarum … (Cambridge, England: 1722), chapter: Editoris notæ ad Harmoniam mensurarum, top of page 95. From page 95: After stating that 180° corresponds to a length of π (3.14159…) along a unit circle (i.e., π radians), Smith writes: "Unde Modulus Canonis Trigonometrici prodibit 57.2957795130 &c. " (Whence the unit of trigonometric measure, 57.2957795130… [degrees per radian], will appear.)
- ^ Isaac Todhunter, Plane Trigonometry: For the Use of Colleges and Schools, p. 10, Cambridge and London: MacMillan, 1864 OCLC 500022958
- ^ Luckey, Paul (1953) [Translation of 1424 book]. Siggel, A., ур. Der Lehrbrief über den kreisumfang von Gamshid b. Mas'ud al-Kasi [Treatise on the Circumference of al-Kashi]. Berlin: Akademie Verlag. стр. 40.
- ^ Cajori, Florian (1929). History of Mathematical Notations
 . 2. Dover Publications. стр. 147–148. ISBN 0-486-67766-4.
. 2. Dover Publications. стр. 147–148. ISBN 0-486-67766-4.
- ^ Muir, Thos. (1910). „The Term "Radian" in Trigonometry”. Nature. 83 (2110): 156. Bibcode:1910Natur..83..156M. S2CID 3958702. doi:10.1038/083156a0
 .Thomson, James (1910). „The Term "Radian" in Trigonometry”. Nature. 83 (2112): 217. Bibcode:1910Natur..83..217T. S2CID 3980250. doi:10.1038/083217c0.Muir, Thos. (1910). „The Term "Radian" in Trigonometry”. Nature. 83 (2120): 459—460. Bibcode:1910Natur..83..459M. S2CID 3971449. doi:10.1038/083459d0.
.Thomson, James (1910). „The Term "Radian" in Trigonometry”. Nature. 83 (2112): 217. Bibcode:1910Natur..83..217T. S2CID 3980250. doi:10.1038/083217c0.Muir, Thos. (1910). „The Term "Radian" in Trigonometry”. Nature. 83 (2120): 459—460. Bibcode:1910Natur..83..459M. S2CID 3971449. doi:10.1038/083459d0.
- ^ Miller, Jeff (23. 11. 2009). „Earliest Known Uses of Some of the Words of Mathematics”. Приступљено 30. 9. 2011.
- ^ Frederick Sparks, Longmans' School Trigonometry, p. 6, London: Longmans, Green, and Co., 1890 OCLC 877238863 (1891 edition)
- ^ 2019 BIPM Brochure
- ^ ISO 80000-3:2006 Quantities and Units - Space and Time
- ^ Hall, Arthur Graham; Frink, Fred Goodrich (јануар 1909). „Chapter VII. The General Angle [55] Signs and Limitations in Value. Exercise XV.”. Написано на Ann Arbor, Michigan, USA. Trigonometry. Part I: Plane Trigonometry. New York, USA: Henry Holt and Company / Norwood Press / J. S. Cushing Co. - Berwick & Smith Co., Norwood, Massachusetts, USA. стр. 73. Приступљено 2017-08-12.
- ^ For a debate on this meaning and use see:Brownstein, K. R. (1997). „Angles—Let's treat them squarely”. American Journal of Physics. 65 (7): 605—614. Bibcode:1997AmJPh..65..605B. doi:10.1119/1.18616., Romain, J.E. (1962). „Angles as a fourth fundamental quantity”. Journal of Research of the National Bureau of Standards Section B. 66B (3): 97. doi:10.6028/jres.066B.012
 ., LéVy-Leblond, Jean-Marc (1998). „Dimensional angles and universal constants”. American Journal of Physics. 66 (9): 814—815. Bibcode:1998AmJPh..66..814L. doi:10.1119/1.18964., and Romer, Robert H. (1999). „Units—SI-Only, or Multicultural Diversity?”. American Journal of Physics. 67 (1): 13—16. Bibcode:1999AmJPh..67...13R. doi:10.1119/1.19185.
., LéVy-Leblond, Jean-Marc (1998). „Dimensional angles and universal constants”. American Journal of Physics. 66 (9): 814—815. Bibcode:1998AmJPh..66..814L. doi:10.1119/1.18964., and Romer, Robert H. (1999). „Units—SI-Only, or Multicultural Diversity?”. American Journal of Physics. 67 (1): 13—16. Bibcode:1999AmJPh..67...13R. doi:10.1119/1.19185.
Литература[уреди | уреди извор]
- E Richard Cohen; Tom Cvitas; Jeremy G Frey; Bertil Holstrom; John W Jost, ур. (2007). Quantities, Units and Symbols in Physical Chemistry (PDF). International Union of Pure and Applied Chemistry (3. изд.). Royal Society of Chemistry; 3rd edition. ISBN 0854044337.
- International Union of Pure and Applied Chemistry (1993). Quantities, Units and Symbols in Physical Chemistry, 2nd edition, Oxford: Blackwell Science. ISBN 0-632-03583-8. Electronic version.















