Рендгенска кристалографија

Рендгенска структурна анализа (РСА) је техника за испитивање кристалних супстанци, која користи дифракциону слику (дифрактограм) добијену расејавањем рендгенског зрачења (X-зрачења) на испитиваном кристалу. Основни циљ РСА је одређивање кристалне и молекулске структуре (дужине веза између атома, углови међу везама, апсолутне конформације...) испитиваног узорка.
Рендгенском структурном анализом могуће је одредити структуру великог броја једињења, која се могу наћи у кристалном облику. За сложенија једињења, као што су различити макромолекули (ДНК, протеини) потребно је комбиновати овако добијене резултате са резултатима добијеним другим аналитичким техникама, као што је нуклеарна магнетна резонанција (НМР), и рачунарским симулацијама да би се добила јасна слика о структури датих једињења.
Кристална структура и микроструктура су у уској вези с физичким и хемијским својствима супстанције, па је важност рендгенске структурне анализе велика у низу грана људске делатности. Утолико је рендгенска структурна анализа нашла бројне примене у физици и хемији чврстог стања, хемији, кристалохемији, биохемији, минералогији и биологији, а изузетну примјену има у металургији, керамичкој, фармацеутској и уопште хемијској индустрији.
Историјски подаци[уреди | уреди извор]
Рендгенски зраци откривени су 1895. године, и име су добили према свом проналазачу, немачком научнику Вилхелму Конраду Рендгену. Прве експерименте са дифракцијом X зрачења на кристалима спровео је Макс фон Лауе 1911. на кристалима соли. Одмах је уочен огроман потенцијал ове методе за одређивање структуре молекула — до тада доступне само преко хемијских и хидродинамичких експеримената. Пионири у развоју рендгенске структурне анализе били су и Вилијам Браг и Бернал. Први протеин чија кристална структура је решена био је миоглобин једне врсте китова и то радовима Макса Перуца и Џона Кендрјуа (1958), за шта су добили Нобелову награду за хемију.

Данас је примена РСА у структурној биологији веома распрострањена — према подацима Протеинске банке података (енгл. Protein Data Bank ,PDB) од око 42.000 протеина чија структура је решена, за око 36.000 је заслужна рендгенска структурна анализа (НМР је допринела са око 6.000 решених структура, затим следе електронска микроскопија, IC спектроскопија...).
Теоријске основе[уреди | уреди извор]
Основни услов који треба испунити да би дошло до дифракције електромагнетног зрачења јесте да таласна дужина зрачења и димензије решетке буду блиске. То је задовољено јер је таласна дужина X-зрачења 10-9-10-11 m, што је истог реда величине као и размак суседних равни у кристалу (1-10 Ǻ).
Када рендгенски зраци падну на кристал атоми или јони почињу да делују као нови, секундарни извори зрачења (Хајгенсов принцип), тј. долази до расипања рендгенских зрака на електронским облацима атома. Између расутих зрака долази до интеракције при чему се део таласа појачава, а део слаби или чак поништава и та појава позната је као дифракција.
Постоје два начина објашњавања феномена дифракције, Брагов закон и Лауеови услови за дифракцију, као и приступ преко реципрочне решетке (Евалдова сфера). Резултати су еквивалентни за различите приступе.
Брагов закон[уреди | уреди извор]
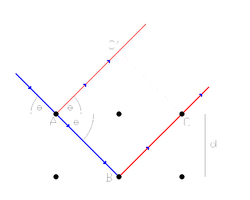
Према Браговом тумачењу, дифракција је еквивалентна рефлексији са система паралелних равни у кристалу. Нека монохроматско зрачење пада на кристал (слика испод). Делом се рефлектује са прве равни, а делом са друге.
Услов за конструктивну интерференцију два овако добијена зрака јесте да је њихова путна разлика једнака целобројном умношку таласних дужина (λ) зрачења:
Из овог услова и геометријских односа добија се Брагов закон:
где је
- n – цео број, ред дифракције
- d – међураванско растојање
- θ – угао који упадно зрачење заклапа са кристалом
Овај закон намеће тачно одређене услове за θ и λ да би дошло до дифракције рендгенских зрака. Различитим експерименталним техникама ове две величине варирају се на различите начине и тако се стварају услови за појаву дифракције на кристалу. Интензитети дифракционих максимума зависе од врсте атома у кристалној решетки и од њиховог међусобног просторног распореда у складу са захтевима симетрије, тј. зависе од кристалне структуре супстанције.
Евалдова сфера[уреди | уреди извор]
Евалдова сфера (сфера рефлексије) је конструкција која даје услов за дифракцију у простору реципрочне решетке кристала. Свака тачка реципрочне решетке одговара једној равни (hkl) реалне решетке, па тако и могућој рефлексији са те равни. Таласни вектор упадног и рефлектованог зрачења (куп и креф) су исте дужине, јер се зрачење расејава еластично. Из Браговог закона за реципрочну решетку видимо да је потребан и довољан услов да до дифракције зрачења дође то да тачка реципрочне решетке лежи на Евалдовој сфери полупречника k (таласни број зрачења које се дифрактује). Експериментално се то постиже ротирањем или осциловањем кристала, јер тада за исти угао ротира или осцилује и реципрочна решетка, па ће многе тачке реципрочне решетке проћи кроз сферу рефлексије и у том тренутку појавиће се дифракциони максимуми.
Кристални узорак је по дефиницији периодичне структуре; кристал је изграђен понављањем елементарне ћелије дуж три независна правца. Сваки дифракциони пик одговара рефлексији са једне равни. Како амплитуда рефлектованог зрачења расте линеарно са бројем рефлексија N са исте врсте равни опажени интензитет пикова расте са N2. У периодичним структурама као што је кристална постоји огроман број паралелних равни (еквивалентне у смислу дифракције) што знатно појачава зрачење добијено рефлексијом и издваја га из шума чинећи га мерљивим. Због непостојања такве врсте уређености регистрован интензитет код аморфних тела или течности је знатно мањи. Још битније, у кристалу молекули имају тачно одређену оријентацију због јаких међусобних интеракција док је у аморфним телима или течностима оријентација молекула случајна или се мења са временом па је опажени сигнал у ствари усредњен сигнал по свим могућим оријентацијама молекула у простору чиме се аутоматски губи било каква информација о структури.
Методе дифракције дају корисне резултате само када се примене на кристалне структуре, јер код материјала неуређених структура (аморфни материјали) доћи ће до расејања зрачења под разним угловима, што ће резултирати да интензитет расејаног зрачења буде подједнак у свим тачкама простора а то не даје никакву информацију о датој структури.
Експерименталне методе РСА-е[уреди | уреди извор]
Принцип извођења РСА-е[уреди | уреди извор]

На узорак (монокристал испитиваног једињења) се усмерава сноп x зрачења. У кристалографији се користе рендгенски зраци таласне дужине око 1 Ǻ добијени помоћу рендгенске цеви. Већина метода рендгенске структурне анализе захтева да зрачење буде што ближе монохроматском. У ту сврху испред или иза узорка на пут рендгенског зрачења се поставља монохроматор (кристал кварца, графита..) или код старијих инструмената филтри од танке металне фолије.
Мењањем θ или λ у зависности од технике остварују се услови за добијање дифракционе слике. Дифракциони максимуми се могу детектовати, снимити, помоћу пропорционалног, сцинтилационог бројача или неког другог детектора или на филму. То је дифракциона слика узорка, у којој су похрањене све информације о структурним особинама узорка, о његовој кристалној структури и микроструктури. Те особине могу се сазнати индицирањем дифрактограма, тј. мјерењем положаја дифракционих максимума и анализом расподеле интензитета дуж дифракционе слике.
Савремени уређаји за снимање дифракционих слика су аутоматски дифрактометри за монокристале и поликристале са одговарајућом софтвер подршком, и могућношћу регулисања услова снимања (температура, притисак), слика 5.
Ако се одреде и интензитети зрачења и фазне разлике у односу на упадно зрачење може се, Фуријеовом трансформацијом, како је ниже објашњено, одредити просторна дистрибуција електронских густина:
ρ (x,y,z)= ΣhΣkΣl Fo(h,k,l) exp(iΦhkl) exp(-2πi(hx+ky+lz))
Позната хемијска структура молекула који сачињава кристал омогућава да из мапе електронске густине добијемо модел кристала са одређеним положајем сваког атома, функционалне групе, структуре, у њему.
Испод је дат преглед метода РСА-е и најзначајније примене.
Класификација експерименталних метода[уреди | уреди извор]
Зависно од врсте узорка и избора експерименталне технике постоје различите методе рендгенске структурне анализе које су приказане у табели 1.
| Узорак | Извор рендгенских зрака | Начин бележења рендгенских зрака | |
|---|---|---|---|
| Лауеова | полихроматски | филм | |
| Ротациона и осцилаторна | монокристал | монохроматски | филм |
| Вајсенбергова | монохроматски | филм | |
| Прецесиона | монохроматски | филм | |
| Дифрактометрија монокристала | монохроматски | детектор | |
| Дебај-Шерерова | Прах | монохроматски | филм (детектор) |
| Гинијеова | монохроматски | филм | |
| Дифрактометрија праха | монохроматски | детектор |
Методе којима се испитује поликристални (прашкасти) узорак првенствено се користе за идентификацију присутних фаза, тј. за квалитативну анализу узорка. Овим методама могу се одредити и прецизни параметри јединичне ћелије, степен кристалинитета узорка, величина кристалита и напони у решетки. Могуће је извести и квантитативну анализу, или пратити фазне трансформације. У новије време дифрактометрија праха се доста користи и за одређивање кристалних структура једињења са вишом симетријом, па чак и за решавање структура свих типва једињења у ab initio поступцима.
Методе којима се испитују монокристали примењују се за одређивање симетрије, просторне групе кристала и за израчунавање параметара решетке. Њихова најзначајнија примена је речавање кристалне структуре једињења.
Одређивање структуре монокристала[уреди | уреди извор]
Велика примена РСА данас је, као што је већ поменуто, у одређивању структуре протеина и других биомолекула. Овде су описани основни кораци у једној таквој анализи протеина. Примењује се метод дифракције на монокристалу, и као што је горе поменуто користи се монохроматско рендгенско зрачење. Користи се монокристал испитиваног једињења.
Услови кристализације[уреди | уреди извор]
Стварање кристала довољно квалитетног за дифракцију (довољно правилна структура) је један од главних проблема у експериментима одређивања атомске структуре протеина. До сада је овај процес слабо разјашњен и добијање доброг кристала своди се више на уметност него на науку. Основна идеја је споро, постепено смањење растворљивости молекула, било снижавањем температуре или повећавањем концентрације раствора. Ако се процес изведе брзо или са неравномерном променом ових величина тј. услова кристализације молекули само преципитују формирајући прах на дну суда.
Процес кристализације састоји се од два ступња: нуклеација (формирање клице) и кристални раст. Услови који одговарају нуклеацији нису увек исти као и они који погодују расту кристала, а у сваком случају је тешко претпоставити оптималне услове за оба. Зато се практично кристализација изводи тако што се припреми велики број раствора испитиваног молекула и затим испробавају различити услови- није ретко да се испробају стотине, чак и хиљаде услова да би дошло до кристализације на одговарајући начин. У услове које варирамо спадају pH, различити адитиви који смањују растворљивост (различите соли Хофмастер серије), или велики полимери (нпр. полиетилен гликол) који извлаче молекуле из раствора ефектом ентропије као и различите почетне температуре раствора. Увек се почиње са врло концентрованим раствором, реда 40 mg/ml протеина.
Традиционалне методе кристализације неорганских једињења модификоване су у циљу примене на протеине, који су термолабилни и осетљиви на високе концентрације органских растварача. Концентровани раствор протеина меша се са различитим растворима који се углавном састоје од:
- Пуфера, због контролисања pH
- Преципитациони агенс, који изазива пресићеност (обично полиетилен гликоли, соли као што су амонијум сулфат или органски алкохоли)
- Друге соли или адитиви, као што су детерџенти или кофактори
Раствор протеина се затим концентрује. Постоје многе методе кристализације које раде на принципу дијализе, дифузија течности, мешања два раствора као и класичне методе испаравања, којима можемо добити кристале испитиваних протеина. Правило је да се корисна информација о структури може добити за кристале који дифрактују са резолуцијом већом од 4 ангстрема (400пм), што је граница за квалитет кристала који желимо да добијемо.
Познати су неки фактори који неповољно утичу на контролисану кристализацију: вибрације или било какве нагле пертурбације, нечистоће. Такође конформационо флексибилни делови молекула инхибирају кристализацију ентропијским ефектима. Молекули који су природно асосовани (нпр. фибриларни протеини) генерално лоше кристалишу. Такође и за кристалографију је проблем асосовање уколико постоји и у кристалу, јер је генерално потребан монокристал. До асосовања молекула обично долази код кристала код којих елементарна ћелија има електрични диполни момент (фероелектрични кристали). У последње време направљени су неки помаци у методама израчунавања који омогућавају одређивање и оваквих структура, мада је то још увек тешко.
Многи биомолекули од интереса нису још увек кристализовани на задовољавајући начин. Несавршености у структури кристала изазване нечистоћама, или постојањем бројних стабилних конформација протеина спречавају добијање слика атомске резолуције. Чак је предложено коришћење Интернационалне свемирске станице у процесу кристализације јер бестежинско стање редукује утицај варијација у температури на формирање кристала.
Снимање дифрактограма[уреди | уреди извор]
Када је формиран, кристал се поставља тако да може да се нађе у снопу x зрака, и да је могуће ротирати га. Има више начина постављања узорка. Један старији је убацивање кристала у стаклену капилару напуњену раствором из којег је кристалисао, и постављање капиларе у дифрактометар. Модернији начин је постављање кристала на танку закривљену жицу и фиксирање мржњењем помоћу течног азота. Ниска температура истовремено редукује оштећења изазвану на узорку због велике енергије џ зрачења, а и минимализује термална кретања која на дифроктограму појачавају шум (Дебај-Велеров ефекат). Проблем је што може доћи до пуцања кристала у струји течног азота па је потребна додатна припрема узорка, која није увек изводљива.
Кристал се затим поставља у дифрактометар који је повезан са извором x зрачења. То може бити или рендгенска цев са стационарном анодом (улаз око 2 kW ЈС), извор типа ротирајуће аноде (улаз око 14 kW ЈС инпут) или синхротон (знатно јачи флукс фотона). При одговарајућим условима долази до дифракције x зрачења, како је горе објашњено, и дифракциона слика се снима на филму или у новије време бележи погодним детектором и преноси на рачунар. Сукцесивне слике добијамо ротацијом кристала у снопу x зрачења.
Пре него што је у експеримент уведено хлађење кристала подаци су добијани на собним температурама. Због горе описаних проблема који се јављају притом (шум) било је потребно извршити многострука мерења за један скуп података што је продужавало време анализе. Данас је време анализе додатно смањено и коришћењем скупа CCD детектора који покривају широк опсег углова истовремено.
Обрада података[уреди | уреди извор]
Основни циљ РСА-е јесте одређивање функције расподеле електронске густине, ф(ρ) у кристалу. Подаци добијени експериментом представљају репрезентацију кристалне решетке у реципрочном простору. Математички је могуће из тога добити изглед решетке у реалном простору.
Фуријеова трансформација[уреди | уреди извор]
Да бисмо то урадили, експериментално прикупљамо податке о Фуријеовој трансформацији ове функције, F(q), коју затим математичким путем обрађујемо да бисмо добили електронску густину у реалном простору. F(q) је структурни фактор који представља релативни интензитет расутог зрачења дуж правца вектора дифракције q, и изражава ефекат релативне позиције честице на расипање. Структурни фактор F(q) је у ствари Фуријеова трансформација структуре.
Важи:
а одговарајућа формула Фуријеове трансформације је:
што ћемо користити даље.
Генерално, функција F(q) је комплексна функција, тј. има поред амплитуде |F(q)|, и фазу Φ(q) :
Интензитети дифрактованог зрачења добијени експериментално су у корелацији са амплитудом |F(q)|. Кориговани интензитет једнак је квадрату амплитуде. Корекциони фактори су температурски, Лоренц-поларизациони, фактор мултиплицитета, и апсорпциони фактор. Међутим интензитет дифрактованог зрачења ни на који начин не зависи од фазе Φ(q).
Може се показати да увек важи:
тј. у општем случају важи F(q) = F(-q), што је познато као Фриделов закон (Friedel), а рефлексије које одговарају q тј. –q називају се Фриделови парови. Као последица важења Фриделовог закона дифракциона слика добијена са било ког кристала увек је централно симетрична, што смањује број експерименталних података које треба прикупити при решавању кристалне структуре.
Проблем фазе[уреди | уреди извор]
Постоји неколико начина да се одреде фазе, тј. реши фазни проблем. У најстарије методе за одређивање кристалне структуре спада метода пробе и грешке. Она се заснива на томе да се претпостави модел структуре, израчунају структурни фактори и упореде са експериментално добијеним. Ова метода може да се користи за једноставније структуре и има углавном историјски значај.
Данас постоји неколико погодних и широко коришћених начина да се релативно брзо и једноставно дође до задовољавајућег почетног модела. Неке методе се заснивају на израчунавању приближних вредности Φ(q) из познатог положаја само једног или неколико атома (Патерсонова функција, метода тешког атома, обично Hg), а друге покушавају да вредности Φ(q) одреде директно (директне методе). За одређивање структура кристала великих органских молекула, као што су протеини и ензими, углавном се користи метода изоморфне замене, и метода снимања аномалија (MAD ,SAD).
Патерсонова (Patterson) функција[уреди | уреди извор]
Врло позната последица Фуријеове трансформације је аутокорелациона теорема која каже да је аутокорелација c(r) функције F(q)
Има Фуријеову трансформацију C(q) која је квадрат амплитуде функције F(q):
Стога аутокорелациона функција C(q) електронске густине (тј. Патерсонова функција) може бити израчуната директно из познатих амплитуда, без познавања фазе. У принципу на овај начин се може директно одредити кристална структура; међутим то је тешко практично реализовати. Аутокорелациона функција одговара расподели вектора међуатомског растојања у кристалу. Стога Патерсонова функција за кристал са N атома у елементарној ћелији може имати N(N-1) максимума. С’ обзиром на неизбежне грешке у мерењу интензитета и математичким проблемима при реконструкцији атомских позиција из вектора међуатомских полођаја и ова техника се користи углавном за решавање структуре једноставнијих кристала.
Модел структуре[уреди | уреди извор]
Када смо добили податак о почетној фази у стању смо да формирамо почетни модел. Координате атома и њихови Дебај-Велерови фактори се фитују према експерименталним подацима. Тиме добијамо нови сет фаза и нову мапу електронских густина. Затим експериментатор прегледа добијене податке, врши корекције на основу искуства или претпоставки и почиње нови круг побољшања на исти начин. То се наставља док се не постигне максимална корелација између експерименталних података и модела.
Када је модел молекулске структуре завршен обично се уноси у неку кристалографску базу података, као што је Протеинска Банка Података, Protein Data Bank (за протеине), или Кембриџ базу података структура, Cambridge Structure Database (за мање молекуле). Многе структуре одређене у приватним, комерцијалним лабораторијама у медицинским истраживањима не налезе се у јавним кристалографским базама података.
Предности и мане[уреди | уреди извор]
Ниједна друге техника откривена до сад не нуди толико података колико РСА, тј. тачније дифракција на монокристалу. Типичан кристал даје 20-30 хиљада рефлексија, где је свака представља један делић укупне информације о структури. Сви ови подаци компјутерском обрадом дају слику расподеле електронске густине са атомском резолуцијом. Захваљујући толиком броју независних података ово и јесте најбоља метода за одређивање атомске структуре било ког молекула.
Међутим, постоје и недостаци, углавном повезани са извођењем експеримента. Прво, потребан је кристал задовољавајућег квалитета, који као што смо видели није лако добити. Неки кристалографи су посветили и више од 10 година свог живота добијању монокристала протеина од интереса, нпр. протеина gp120 који вирус HIV –а користи да би ушао у људску ћелију. Такође битан недостатак је и то што на овај начин не добијамо слику молекула у свом природном окружењу, што је битно код биомолекула. Добијена структура је просечна структура, а немамо ни информацију о рецимо мобилности и покретљивости протеина.
Литература[уреди | уреди извор]
- Љ. Карановић, Д. Полети, ‘Рендгенска структурна анализа’, Завод за уџбенике и наставна средства, Београд,2003
- Staff,’ Introduction to X-ray Diffraction’, Materials Research Laboratory, University of California, Santa Barbara.
- W.L. Bragg, "The Diffraction of Short Electromagnetic Waves by a Crystal", Proceedings of the Cambridge Philosophical Society, 17 (1912), 43–57.
- Ewald, P. P., editor ‘50 Years of X-Ray Diffraction’ (Reprinted in pdf format for the IUCr XVIII Congress, Glasgow, Scotland, Copyright © 1962, 1999 International Union of Crystallography).
- McPherson, A (1999). Crystallization of Biological Macromolecules. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press. ISBN 978-0-87969-617-7.
- Drenth J. Principles of Protein X-Ray Crystallography. Springer-Verlag Inc. NY. 1999. ISBN 978-0-387-98587-9..
- Glusker JP, Lewis M, Rossi M. Crystal Structure Analysis for Chemists and Biologists. VCH Publishers. NY:1994. ISBN 978-0-471-18543-7..
- Rhodes G. Crystallography Made Crystal Clear. Academic Press. CA. 2000. ISBN 978-0-12-587072-6..
Спољашње везе[уреди | уреди извор]
- Кристализација малих молекула (језик: енглески)








