Хидрауличне турбине
Хидраулична турбина је ротациона машина која хидрауличну енергију, насталу струјањем воде - трансформише у механички рад. У данашње време хидрауличне турбине се најчешће користе за покретање генератора и добијање електричне енергије из обновљивих (хидрауличних) извора енергије.[1][2]
Развој хидрауличних турбина[уреди | уреди извор]


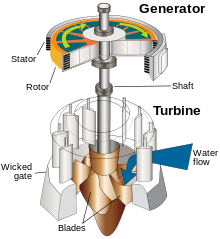
Вековима људи користе хидроенергију како би добили механички рад. У Старом веку су коришћена обртна кола, која су покретали брзи водотокови, а која су служила за погон млинова. У неким, забаченијим деловим света, и дан данас се користе овакве конструкције, првенствено због једноставности, за погон млинова.
- Око 1750. године професор Јохан Андреас Зегнер (франц. Segner János András) је конструисао прво водно коло засновано на реакцијском принципу - Зегнеров точак. Оптимални хидралични степен корисности Зегнеровог точка је био око 52%, што је веома мало у односу на данашње хидрауличне степене корисности модерних великих хидрауличних турбина који се крећу до 95%.
- 1750. године Леонард Ојлер поставља основну теорију реакцијских водних турбина у делу „Потпуна теорија машина које се покрећу реакцијом воде“). Већ 1754. године је дао и сопствену конструкцију турбине која је имала хидраулични степен корисности око 71% (Ојлерова турбина је направљена 1943. године у Цириху, а затим и испитана).
- Француски инжењер Клод Бурден (енгл. Claude Bourdin) је почетком 19. века побољшао Зегнерово коло и први пут га назвао турбином. Овакво коло постоји и дан данас, с тим што се уместо водне користи енергија чврстих горива.
- 1827. године француски инжењер Бено Фурнејрон (енгл. Benoît Fourneyron) конструише прву „употребљиву“ турбину. У питању је била радијална центрифугална турбина са спроводним апаратом и могућношњу регулације турбине варирањем протока при константном нето паду турбине.
- 1837. године Карл Антон Хеншел (енгл. Carl Anton Henschel) је дизајнирао прву аксијалну турбину, коју је касније, 1843. године патентирао Николас Жонвал (енгл. Nicolas J. Jonval). Ова турбина је имала претечу сифона.
- 1838. године Американац Семјуел Хауд (енгл. Samuel Howd) је конструисао турбину веома сличној данашњој Франсисовој турбини која је постигла веома велики степен корисности - око 70%.
- 1868. године Американац Џејмс Бишено Франсис (енгл. James Bicheno Francis) је урадио нову конструкцију Хаудове турбине и постигао висок степен корисности - 86%. Од тада се све турбине овог типа зову Франсисове турбине.
- 1878. године немачки професор Р. Финк је унапредио регулисање код Франсисових турбина конструкцијом покретних спроводних усмерних лопатица. Пре тога су Франсисове турбине регулисане на разноразне примитивне начине који су кварили струјно поље на улазу у турбину и производили велике хидрауличне губитке.
- 1880. године Лестер Пелтон (енгл. Lester Pelton) конструише турбину погодну за велике падове. Касније су ове турбине назване Пелтонове турбине.
- Крајем XIX века почиње нагли развој турбина у правцу брзоходости. Овај развој је проузрокован применом турбина за добијање електричне енергије - биле су потребне турбине за велике протоке са малим падовима. Захваљујући Николи Тесли дошло је до велике примене хидрауличних турбина у добијању електричне енергије. Тежње ка већој брзоходости водиле су ка мањем броју обртаја турбина што је водило ка проблему у преносу снаге до генератора. Овај проблем је актуелан и данас, али је ублажен прозводњом савремених вишеполних генератора који се данас примењују уместо комбинације огромног мултипликатора и генератора са малим бројем полова. Како су произвођачи генератора избегавали производњу вишеполних генератора развој турбина у погледу брзоходости је заустављен, а пројектанти хидромашинских инсталација на хидроелектранама су се довијали уградњом вишеструких турбина са хоризонталним вратилом.
- 1913. и 1914. године аустријски инжењер Виктор Каплан (Viktor Kaplan) пријављује велики број својих патената од којих су најбитнија следећа три:
- Обртно коло са аксијалним притицањем воде (лопатице се простиру радијално).
- Примена Финковог спроводног апарата и стварање великог безлопатичног простора у коме вода скреће за 900, тј. из радијалног у аксијални правац.
- Примена лопатица обртног кола које се могу покретати око своје радијалне осе.
- Каплан је урадио испитивања у лабораторији фирме Фоит у Хајденхајму 1917. године, међутим пропелерно коло није било довољне крутости па су се лопатице савијале под оптерећењем. Добијени резултати су били незадовољавајући па је фирма Фоит одустала од даљег истраживања. Каплан 1919. године склапа уговор са фирмом Шторек из Брна и убрзо гради прву хидроелектрану са Каплановом турбином. Након почетног успеха фирма Шторек доживљава низ неуспеха градећи хидролелектране по упутствима Каплана, који је своје турбине пројектовао без довољно података, па је при максималним протоцима долазило до интензивне кавитације турбина. Тек касније је Дитер Тома, професор Високе техничке школе у Минхену, дао објашњење феномена кавитације и дефинисао услове кавитацијског стања увођењем кавитацијског коефицијента.
- Цевне турбине су развијане такође почетком XX века и представљају варијацију Капланове турбине с тим да су ово најбрзоходије турбине прилагођене равничарсим рекама са великим протоцима и малим падовима. Руски извори тврде да је њихов инжењер, извесни Графтио уградио по свом патенту цевну турбину на ХЕ „Нева“ још 1912. године. Фабрика Ешер Вис је изградила ХЕ „Ростин“ у Пољској, са уграђеним цевним турбинама 1936. године. Ове турбине су имале непокретни спроводни апарат, али покретне лопатице радног кола.
- Негде у периоду од 1950. до 1953. године развијене су тзв. дијагоналне турбине које се брзоходости надовезују на Франсисове турбине. Ове турбине су такође варијација Капланове турбине. Прва турбина овог типа уграђена је на хидроелектрану „Сер Адам Блек“ на Нијагари 1957. године. Ова турбина је могла радити као пумпа па представља једну од најстаријих реверзибилнх хидроелектрана на свету.
Закључак који се намеће је да не постоји универзални тип турбине који ће искористити све падове и протоке, већ да се за сваки конкретан случај потребна посебна турбина. Ову чињеницу су професори Машинског факултета у Београду др Мирослав Бенишек и покојни Никола Обрадовић, дипл. маш. инж. духовито истицали: Турбина је одело по мери.
Класификација хидрауличних турбина[уреди | уреди извор]
У зависности од начина претварања струјне енергије у механичку, турбине се могу поделити на:
- Акцијске турбине које користе само кинетичку енергију млаза, док притисна енергија остаје скоро непромењена од улаза до излаза из радног кола. Други назив за ове турбине је слободомлазне турбине. У ову групу спада Пелтонова турбина, Турго турбина која представља модификацију Пелтонове турбине, ...
- Реакцијске турбине код којих се у радном колу мењају све три компоненте струјне енергије (притисна, кинетичка и положајна). Код ових турбина притисна енергија је већа на улазу него на излазу па се због тога називају и притисним турбинама. У ову групу спадају Франсисове, аксијалне Капланове, аксијалне цевне и дијагоналне турбине.
Током времена развој и експериментална истраживања хидрауличних турбина су довела до важног закључка: Немогуће је са једним типом турбине остварити квалитетну размену енергије за све протоке и падове. Тако су се из читавог скупа разних развијаних турбина развила четири основна типа:
 |
 |
 |
 |

Облик кола и конструкција турбине зависе од специфичне брзине обртања . За доношење одлуке о примени појединих типова турбина користе се разни типови дијаграма:
- Сводни дијаграм по руској номенклатури у функцији (Н, Р) према искуству великих фирми.
- Дијаграм према препорукама фирме Фојт Хидро.
- Дијаграм према препорукама фирме Силцер.
Избор типа кола зависи и од параметара електране. Тако се нпр. код конструисања реверзибилног агрегата машина пројектује као пумпа при чему се води рачуна да она треба да ради и као турбина.
Класификација турбина у зависности од специфичне брзине обртања:
- Пелтонове турбине - Н=100÷2000m; Спороходе: =4÷15, број млазница: 1÷2; Нормалне: =15÷25, број млазница: 2÷4; Брзоходе: =25÷60, број млазница: 5÷6.
- Франсисове турбине - Н=40÷700m; Спороходе: =80÷150; Нормалне: =150÷250; Брзоходе: =250÷450.
- Дијагоналне турбине - Н=30÷200m; Спороходе: =230÷280; Нормалне: =280÷340; Брзоходе: =340÷500.
- Аксијалне турбине - Н=3÷80m; Спороходе: =350÷450; Нормалне: =450÷650; Брзоходе: =650÷1100.
Савремене хидрауличне турбине имају савршене конструкције и високе вредности степена корисности који достижу и 95%, па спадају групу машина са највишим степенима корисности те се могу поредити са великим електричним моторима и генераторима.
Основни параметри хидрауличних турбина[уреди | уреди извор]
Основни параметри хидрауличних турбина су:
- Проток турбине Q [m3/s] представља ону количину воде која протекне у једној секунди кроз турбину. Треба га разликовати од протока кола турбине Qk који је мањи од Q.
- Бруто јединични струјни рад Ybr [J/kg]=g [m/s2] Hbr [m] електране представља разлику укупних једничних енергија горњег и доњег нивоа воде у акумулацији и доњој води. Величина Hbr се назива бруто пад електране.
- Нето јединични струјни рад турбине Yn [J/kg]=g [m/s2] Hn [m] представља укупну разлику јединичних струјних енергија на излазу и улазу из турбине. У пракси се чешће користи величина нето пад турбине Hn. У литератури се нето пад турбине углавном означава са Н без индекса „n“. Рачунски нето пад турбине Нr се одређује пре самог пројектовања турбине на основу протока, димензија електране, и др. Веза између Нbr и Нn су хидраулични губици од акумулације до улаза у турбину и од излаза из турбине до доње воде.
- при чему су и хидраулични губици у „енергетским“ метрима.
- Хидраулична снага турбине Рh [W] је она количина рада у јединици времена коју би вода разменила у турбини када не би било губитака:
- где је [kg/m3] густина воде.
- Снага турбине је снага добијена на спојници турбине:
,
- где је Pi унутрашња снага турбине, Pgm механички губитак снаге у лежиштима и заптивачима, η укупан степен корисности турбине.
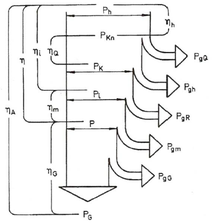
- Постоји још и снага кола сведена на проток кроз турбину PKn, снага кола Pk, снага потребна за савлађивање отпора на спољашњим површинама кола PgR и снага генератора (видети слику „Биланс снаге“).
- Укупан степен корисности η [-]. Постоји још хидраулични ηh, волуметријски ηQ, унутрашњи ηi, механички степен корисности ηm, те степен корисности генератора ηG и степен корисности агрегата ηA (видети слику „Биланс снаге“).
- Брзина обртања кола турбине n [min-1], тј. угаона фреквенција кола турбине ω [s-1]. Веза између ω и n:
- Велике турбине које су спојене са синхроним генератором наизменичне струје морају се окретати сталном брзином како би фреквенција мреже f [Hz] имала сталну вредност (у Европи 50Hz, а у Америци 60Hz). Фреквенција, број пари полова генератора p и брзина обртања су повезани следећим изразом:
- Из ових израза се види је синхрона брзина обртања за фреквенцију у мрежи од 50Hz одређена следећим изразом:
- Кавитациони коефицијент σ [-] дефинише кавитацијско стање турбине (да ли се у радном колу јављају мехурови водене паре). Моделским испитивањем се утврђује која је вредност кавитационог коефицијента испод кога не сме да се иде (σkr) јер ће у противном долазити до кавитацијских оштећења.
Теоријске основе хидрауличних турбина - Ојлерова једначина за турбине[уреди | уреди извор]
Теорија турбина је заснована на основним једначинама механике флуида:
- Једначини континуитета
- Једначини струјања вискозног флуида
- Једначини енергије
- Једначини промене количине кретања, тј. Навије-Стоксовим једначинама
Средином XVIII века Ојлер је извео једначину за турбомашине - турбине која је допринела далеко бољем разумевању процеса размене енергије у турбинама:
при чему су: u1 - преносна (обимска) брзина на улазу у коло, cu0 - апсолутна брзина на улазу у коло u2 - преносна (обимска) брзина на излазу из кола cu3 - апсолутна брзина на излазу из кола r1 - полупречник кола на улазу, r1 - полупречник кола на излазу.
Други облик Ојлерове једначине:
указује на услове који морају да буду испуњени да би се у турбинском колу разменила енергија:
- Флуид мора испуњавати струјни простор,
- коло се мора обртати и
- мора постојати коначна разлика циркулације од улаза до излаза из кола
Закони сличности хидрауличних турбина. Значице хидрауличних турбина[уреди | уреди извор]
Моделска испитивања турбина су далеко јефтинија од цене могућег промашаја приликом израде велике турбине, па се експериментална истраживања врше у хидрауличким лабораторијама на моделима турбина геометријски сличним великим турбинама у хидроелектранама (оне се називају и главно извођење или прототип). Резултати добијени моделским испитивањем се своде на карактеристичне величине - значице, које представљају једнозначну зависност основних величина утврђених помоћу закона сличности механичких система.
Услов потпуне динамичке сличности два струјна поља, за модел и главно извођење, јесте једнакост свих бројева сличности:
где су Sh, Fr, Eu, Re Струхалов, Фрудов, Ојлеров и Рејнолдсов број, респективно. Индекси „m“ и „p“ се односе на модел, односно на прототип.
Потпуна динамичка сличност, а тиме и горњи услови не могу бити задовољени. Покушај задовољења свих услова доводи до контрадикторних услова.
Нпр. Покушај задовољења једнакости Фрудових () и Рејнолдсових () бројева ће довести до следеће контрадикторности:
- За испуњење захтева при истој кинематској вискозности флуида мора да буде испуњен услов да су брзине Cm>Cp, пошто је D1m<D1p, док за испуњење једнакости Фрудових бројева при Gm=Gp=g (убрзање Земљине теже) мора да буде испуњен услов да су брзине Cm<Cp узевши у обзир да и даље важи D1m<D1p!
Не само да није могуће остварити потпуну динамичку сличност, већ је немогуће остварити и потпуну геометријску сличност прототипа и модела коју би требало најлакше остварити:
Покушај да се све димензије прототипа преведу преко преводног коефицијента геометријске сличности на модел, доћи ће се до тога да све димензије прототипа могу да се смање за нпр. 10 пута, али површинска храпавост модела неће моћи да се смањи исто толико, јер модел неће моћи да се обради ништа боље од прототипа.
Једнакост Рејнолдсових бројева такође не може да се оствари управо због релативне храпавости која утиче на неједнакост бездимензијских хидрауличних губитака енергије у моделу и прототипу. Све ово доводи до неједнакости хидрауличких степена корисности модела и прототипа!
Из једнакости бездимензијских бројева за модел и прототип долази се до одређених величина - значица од којих неке имају димензију, а неке немају:
- Из једнакости Ојлерових бројева долази се до јединичног протока - то је проток условно изабране турбине која има пречник 1m и ради на паду од 1m. Ова величина је димензијска [m0.5/s], али се често у пракси узима јединица протока [m3/s]:
- Из једнакости Струхалових бројева долази се до јединичне фреквенције обртања кола - то је фреквенција обртања кола турбине која има пречник од 1m и јединични струјни рад од 1[J/kg]:
- У техничкој пракси се уместо f11 чешће користи друга димензијска величина - јединични број обртаја која је бројно једнака броју обртаја условно изабране турбине пречника 1m која ради на паду од 1m. Често се за димензију ове величине узима min-1.
- Из израза за унутрашњу снагу турбине и једничног протока турбине долази се до јединичне снаге турбине која је бројно једнака снази на вратилу турбине пречника 1m која ради на паду од 1m.
- Из израза за јединичну фреквенцију и израза за обртни момент на вратилу турбине (M=Pi/ω) се долази до јединичног момента који је бројно једнак моменту на вратилу условно изабране турбине која има пречник 1m и ради на паду од 1m.
Последњих година уведене су другачије значице које директно зависе од Ојлеровог и Струхаловг броја. Ове значице су у правом смислу речи бездимензијски бројеви:
- Значица јединичног струјног рада кола:
- Значица јединичног струјног рада турбине:
- Значица протока кола турбине:
- Значица протока турбине:
- Значица снаге кола турбине:
- Значица снаге турбине λ.
Специфична брзина обртања, значица брзоходости и значица пречника[уреди | уреди извор]
Кроз време се показало да значице n11, Q11 и ψ свака посебно не могу дефинисати геометријски облик турбине. Међутим, међусобни, односно функционални однос значица φ и ψ, тј. n11 и Q11 или n11 и P11 дефинисани за тачно одређену погонску тачку (номиналну) турбине одређује тип турбине. Однос ових функционалних значица обједињује све битне параметре турбине: проток, пад, снагу и брзину обртаја и представља општи показатељ који означава тип турбине.
- Специфична брзина обртања - брзоходост је бројно једнака брзини обртања n условно изабране турбине која на паду од 1m даје снагу од Pi=1kW:
- У техничкој пракси се поред ове величине може користити и nsQ, која се такође зове специфични број обртаја, а дефинише се као:
- У литератури се често користи уместо nsQ следећа значица - специфична фреквенција која је бројно једнака фреквенцији обртања кола условно изабране турбине која ради са јединичним струјним радом од 1J/kg и протоку од 1m3/s:

- Комбинацијом наведених израза долази се до:
- Величина σ* се назива значицом брзоходости и има исти значај као специфични бројеви обртаја nsp и nsQ у одређивању типа турбине.
- Повезујући значицу напора и значицу протока тако да се притом елиминише број обртаја, а задржи линеарна зависност од пречника турбине D1 долази се до значице пречника:
Истраживања Кордиеа су показала да се тип турбомашине, а тиме и турбине може дефинисати на основу значица брзоходости и пречника. Ове две значице одређују тип турбомашине било она турбина, пумпа или компресор.
Прерачунавање степена корисности са модела на прототип турбине[уреди | уреди извор]
Хидраулички степен корисности зависи од карактеристичних величина турбине и може се написати у облику следеће зависности:
при чему су: δ - апсолутна храпавост проточних површина, s - величина процепа, D1 - пречник кола турбине.
Како је за апсолутну сличност модела и прототипа потребно остварити да горњи израз буде исти за модел и прототип, а то је немогуће, долази се до следећег запажања:
где је Δηh поправка хидрауличког степена корисности у односу на модел.
Увећање степена корисности прототипа у односу на модел назива се ефектом размере
До данашњих дана многи истраживачи раде на овом проблему, али нико није дошао до адекватног решења зог сложености струјања у самом проточном тракту турбине. Задовољавајући поступак прерачунавања степена корисности би требало да реши проблем са максималном апсолутном грешком од 0,1% у свим погонским тачкама турбине. Овај поступак није нађен тако да се истраживања и даље настављају како би се избегла веома скупа гаранцијска испитивања на хидроелектранама.
Формуле за прерачунавање се могу сврстати у три групе:
- Прва група формула је узимала у обзир само губитке на трење, занемарујући притом све остале хидрауличне губитке. Ове формуле иако спадају у ред једноставнијих формула по својој структури имале су донекле коректне, више подстицајне резултате у области оптималних погонских тачака турбина. Ове формуле датирају из прве половине XX века (од Камерерове из 1910. године до Нехлебине из 1949. године).
- Друга група формула је узимала укупне хидрауличне губитке као збир губитака на трење и вихорних губитака (они имају карактер локалних губитака: одлепљивање струје, вртложење, ...). формуле друге групе су прерачунавале губитке на трење са модела на прототип, али су вихорни губици остајали неизмењени. Оне јесу побољшање прерачунавања, али само у области оптимума, док у областима ван оптималних степена корисности дају нереалне резултате. Неки од аутора формула друге групе су Етинберг, Канан, Акерет, ...
- Трећа група формула је настала из потребе да се степен корисности прерачунава не само у оптимуму, већ у ширем дијапазону вредности. Ова група формула је покушај за изналажење поступка за прерачунавање који узимају у обзир положај радне тачке турбине дефинисан са (n11, Q11) или (Q, H). У ову групу формула спадају формула Шчапова, Етинберга, Института ЦКТИ, Остервалдера, инжењера ЛМЗ-а (њихова формула је потврђена на ХЕ „Ђердап II“). Радна група ИЕЦ (Интернационална електротехничка комисија) је предложила 1985 године формулу за прерачунавање, међутим треба рећи да ни ова формула не даје коректне резултате за све турбине у широкој радној области.
Кавитација у хидрауличним турбинама[уреди | уреди извор]

Кавитација је динамички процес у струји течности који се карактерише настајањем гасно - парних мехурова и њиховим наглим нестајањем (каже се да су мехурови имлодирали). Временски интервал имплозије мехурова је реда 1 μs, а локални притисак расте и до 104 бара (109 Pa). Кавитација, у њеном развијеном стадијуму, у хидрауличним турбинама изазива следеће:
- Мења структуру струјања.
- Погоршава степен корисности и снагу турбине (снага турбине се снижава како се смањује степен корисности, проток а и нето пад јер се губици у колу повећавају).
- Ствара карактеристичан шум - кавитациону буку.
- Кавитационе имплозије уништавају зидове проточног тракта - тзв. кавитациона ерозија.
- Кавитациони удари могу изазвати вибрације не само хидроагрегата, већ и читаве хидроелектране.
Кавитацијски коефицијент турбине σТ се одређује из следећег израза:
,
при чему су:
- коефицијент притиска у тачки М (на лопатици) где притисак има минималну вредност
- степен корисности сифона
- компонента (меридијанска) апсолутне брзине на излазу из кола
- релативна брзина на излазу из кола
- релативна брзина у тачки М (тачка где је најнижи притисак) на лопатици кола
Уводи се σ - коефицијент кавитацијске резерве постројења који зависи од положаја турбине у односу на доњу воду (код неких аутора се он обележава са Th и назива Томин број по Дитеру Томи који је први извео израз за σ):
при чему су:
pb - барометарски притисак
- притисак засићења водене паре (t - температура воде у [oC])
HS - усисна висина, односно дубина потапања
- брзина на излазу из сифона
NPSY - net positive suction energy
NPSH - net positive suction head
Могу наступити три случаја:
- σ>σT - нема кавитације
- σ=σT - почетна кавитација
- σ<σT - интензивна кавитација
Карактеристике хидрауличних турбина[уреди | уреди извор]
Карактеристике турбина приказују аналитичку или графичку (ово је чешћи случај) зависност геометријских, енергетских и кавитацијских параметара одређеног типа турбине. Оне се одређују на моделима и прерачунавају се на прототип. Каснијим мерењима на прототипу се потврђују карактеристике (гаранцијска испитивања).
Турбине могу бити јединачне регулације или двојне регулације, зависно од тога да ли је регулација протока могућа само на један начин (преко копља у млазници код Пелтонове турбине, лопатицама спроводног апарата код Франсисове турбине, ...) или на два начина (закретањем лопатица спроводног апарата и истовременим закретањем лопатица обртног кола - Капланове, цевне и дијагоналне) који су везани тзв. комбинаторском везом:
где су:
- отвор спроводног апарата
- угаони положај лопатица кола
Комбинаторска веза представља везу између отвора спроводног апарата и отвора лопатица кола и нето пада за највиши степен корисности у тој погонској тачки.
Регулисање протока код хидрауличних турбина[уреди | уреди извор]
Значајнија промена снаге турбине се може остварити само променом протока, с тим што треба узети у обзир да се променом протока мењају и енергетски и кавитациони параметри турбина. Проток кроз турбину зависи од:
- Геометријских размера турбине,
- Облика струјног тока у проточном делу
- Брзине обртања турбине
- Јединичног струјног рада
- ηh и ηQ
Могући су следећи начини регулисања протока:
- Закретањем лопатица спроводног апарата (Франсисове и пропелерне турбине)
- Закретањем лопатица радног кола (турбине које имају овакав начин регулације називају се Капелерне турбине)
- Истовременим закретањем лопатица спроводног апарата и радног кола. Функционална веза између положаја лопатица спроводног апарата и положаја лопатица радног кола назива се комбинаторска веза.
Начини регулисања под 1 и 2 називају се јединачном регулацијом, а начин 3 двојном регулацијом.
Осим ових, наведених, начина регулисања протока, постоје и други начини, мање економични, али једноставнији, који се користе код мањих турбина.
Облици карактеристика хидрауличних турбина[уреди | уреди извор]
Опште зависности облика:
се могу представити у једноставнијим облицима, при чему ће се поједине величине сматрати независним променљивим док ће међу осталим променљивим постојати функционална зависност. Овакве зависности називају се јединачне карактеристике. У зависности од величине која се наноси на апсцису могу се дефинисати следеће линијске карактеристике:
- * Карактеристика брзине обртаја
- * Карактеристика протока
- * Карактеристика пада
- * Карактеристика снаге
 |
 |
 |
 |
Линијске карактеристике служе као међукорак ка конструисању веома сложених зависности турбина - универзалних карактеристика.

Помоћу бездимензијских линијских карактеристика (на слици је приказана промена бездимензијског степена корисности у зависности од бездимензијског протока) могуће је упоредити различите типове турбина: Пелтонову, Капланову, Франсисову и пропелерну, при чему је:
где су: , вредности степена корисности и протока у оптималној радној тачки. Са дијаграма се види да Пелтонова и турбине са комбинаторском везом могу радити у широком подручју ван оптималног протока.

Потпуну слику о енергетским и кавитацијским особинама турбина дају тзв. топографски дијаграми (шкољкасти дијаграми или пасош турбине). Универзалне карактеристике се добијају експерименталним испитивањима модела турбина на опитним постројењима на основу прописа IEC. Само име ових карактеристика, односно дијаграма, говори нам о својствима ових карактеристика:
- * Универзална - означава општу важност карактеристике за све турбине које задовољавају геометријску сличност,
- * Топографски (шкољкасти) - упућује на облик линија истог степена корисности које личе на топографске изохипсе,
- * Пасош - упућује на својство карактеристика да дају све битне податке по којима се геометрија турбина распознаје.
Карактеристике побега агрегата[уреди | уреди извор]
У нормалним радним условима брзина обртања турбине је константна, јер систем за регулацију обезбеђује једнакост хидрауличког момента и момента кочења турбине који је збир момента на вратилу генератора и момента сила трења. У случају повећања хидрауличног момента (или момента кочења), регулатор смањује (повећава) отвор спроводног апарата чиме смањује односно повећава проток кроз турбину, а самим тим мења и хидрауличку снагу, тј. враћа брзину обртања на задату вредност.
У случају када наступи 100%-тно растерећење турбине (MG=0) - хаваријски услови, односно распад електричне мреже, при неисправном регулатору или блокади система за регулисање долази до наглог повећања брзине обртаја ротационих делова турбине. Веома брзо успоставља се нова природна равнотежа хидрауличног момента и момента сила трења, али без дејства регулатора и тада ротор достиже максималну брзину обртања за затечени отвор спроводног апарата и радног кола. Ова појава назива се залетом или побегом, а често се каже да се турбина отела. Максимална брзина обртања назива се брзином обртања побега. При побегу се сва хидраулична енергија користи за савлађивање губитака у турбини. Ова брзина се одређује моделским испитивањима на опитним постројењима. При побегу турбине расту обимске брзине у обртном колу што изазива погоршање услова струјања и значајно повећање хидрауличних губитака у ортном колу и сифону турбине. Због нерегуларности у условима струјања долази до повећаних вибрација. Такође, са повећањем брзине обртања расту и центрифугалне силе у елементима турбина, тј. напони у материјалу који достижу и неколико пута веће вредности од номиналних. Све ово указује на побег као непогодну и крајње нежељену појаву, па је приликом конструисања турбине брзину побега потребно свести на најмању могућу вредност. Уобичајено је да се приликом конструисања турбине пази да напони на елементима турбине не пређу 0,9σpl при фреквенцији побега.
Остале карактеристике турбина[уреди | уреди извор]
У остале, не мање важне карактеристике од горе наведених карактеристика спадају:
- * Кавитационе карактеристике (одређују се експерименталним испитивањима на моделима турбине)
- * Експлоатационе карактеристике (конструишу се за прототип турбине и имају практичну употребну вредност у експлоатацији)
- * Кружне карактеристике (приказују све могуће погонске ситуације турбине)
- * Универзалне четвороквадратне карактеристике турбине
- * Сутеров дијаграм (погодан за прорачуне помоћу рачунара)
Проточни делови турбина[уреди | уреди извор]
Проточни простори реакцијских турбина се састоје од следећих делова:
- Уводних комора
- Прстена статорских лопатица
- Спроводног апарата
- Обртног кола
- Сифона
Референце[уреди | уреди извор]
- ^ Мирослав Бенишек (1998). Хидрауличне турбине. Машински факултет у Београду. ISBN 86-7083-323-9.
- ^ Скрипте са предавања из Хидрауличних турбина на Машинском факултету у Београду, 2002/2003
Литература[уреди | уреди извор]
- Мирослав Бенишек (1998). Хидрауличне турбине. Машински факултет у Београду. ISBN 86-7083-323-9.














































![{\displaystyle p_{d}=133.333exp\left[18.5916-{\frac {3991.11}{t+233.84}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79e81b37d7b38bc3765c8aa286ee626b924ad79d)










