Релоов троугао

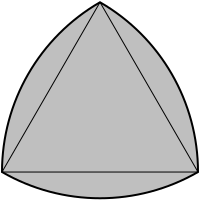
С Википедије, слободне енциклопедије

Релоов троугао је слика са константним пречником, базирана на једнакостраничном троуглу. Растојања од било које тачке криве до супротног темена су сва иста.

Релоов полигон је крива константне ширине - то јест, крива чији су сви пречници исте дужине.[1] Најпознатиији облик је Релоов троугао. Име је добио по Францу Ролоу, немачком инжењеру из 19. века, мада је троугао био познат и пре њега. Релоов троугао је најпростији нетривијални пример криве са константном ширином - крива код које су иста растојања две супротне паралелне тангенте, небитно од смера тих паралела. (Тривијални пример је круг.)

Релоов полигон се формира од пресека три кружна диска, од којих сваки има центар на граници друга два. Константна ширина значи да је раздвајање сваке две паралелне носеће линије исто, независно од њихове оријентације. Пошто су сви његови пречници исти, Релоов троугао је један одговор на питање „Осим круга, какав облик може да поприми поклопац шахта тако да не може да падне кроз рупу?“[2]

Релоови троуглови се такође називају сферним троугловима, али тај термин се тачније односи на троуглове на закривљеној површини сфере. Они су названи по Францу Ролоу,[3] немачком инжењеру из 19. века који је био пионир проучавања машина за превођење једне врсте кретања у другу, и који је користио Ролоове троуглове у својим дизајнима.[4] Међутим, ови облици су били познати пре његовог времена, на пример од стране дизајнера готских црквених прозора, од Леонарда да Винчија, који их је користио за пројекцију карте, и од Леонарда Ојлера у својој студији облика константне ширине. Остале примене Релоовог троугла укључују давање облика трзалицама за гитару, наврткама за хидрант против пожара, оловкама и бургијама за бушење квадратних рупа са филетом, као и у графичком дизајну у облику неких знакова и корпоративних логотипа.

Међу облицима константне ширине са датом ширином, Релоов троугао има минималну површину и најоштрији (најмањи) могући угао (120°) у својим угловима. По неколико нумеричких мера, он је најудаљенији од централно симетричног. Он обезбеђује највећи облик константне ширине избегавајући тачке целобројне решетке и уско је повезан са обликом четвороугла максимизирајући однос периметра и пречника. Он може да изврши потпуну ротацију унутар квадрата док у сваком тренутку додирује све четири стране квадрата и има најмању могућу површину облика са овим својством. Међутим, иако покрива већину квадрата у овом процесу ротације, не успева да покрије мали део површине квадрата, близу његових углова. Због ове особине ротације унутар квадрата, Релоов троугао је понекад познат и као Релоов ротор.[5]

Конструкција[уреди | уреди извор]

Релоов троугао који ротира у квадрату константних димензија

Конструкција Релоовог троугла почиње на једнакостраничном троуглу.[6] Шестар се постави у једно од темена и опише кружни лук између друга два темена.[7] То се понови и за остала темена. Затим се обрише почетни троугао. Резултат је крива са константном ширином. Еквивалентно, за дати троугао Т чије су странице а, узети границу пресека кружница са полупречником а које су конструисане из темена Т.

По Блашке-Лебеговој теореми, Релоов троугао има најмању површину од свих кривих константне ширине. Та површина је , где је r константни полупречник.

Релоов троугао може да се генерализује на правилне полигоне са непарним бројем страница. Тако су, на пример, израђени британски новчићи од 20 и 50 пенија.

Математичка својства[уреди | уреди извор]

Паралелне носеће линије Ролоовог троугла

Најосновније својство Ролоовог троугла је да има константну ширину, што значи да за сваки пар паралелних носећих линија (две линије истог нагиба које обе додирују облик без да прелазе кроз њега) две праве имају исто међусобно Еуклидско растојање, без обзира на оријентацију ових линија.[8] У било ком пару паралелних носећих линија, једна од две праве ће нужно додирнути троугао у једном од његових врхова. Друга потпорна линија може додирнути троугао у било којој тачки супротног лука, а њихово растојање (ширина Ролоовог троугла) је једнака полупречнику овог лука.[9]

Први математичар који је открио постојање кривих константне ширине и приметио да Ролоов троугао има константну ширину, вероватно је био Леонард Ојлер.[5] У раду који је представио 1771. и објавио 1781. под насловом De curvis triangularibus, Ојлер је проучавао криволинијске троуглове као и криве константне ширине, које је назвао орбиформама.[10][11]

Екстремне мере[уреди | уреди извор]

По многим различитим мерама, Релоов троугао је једна од најекстремнијих кривих константне ширине.

По Блашк-Лебеговој теореми, Ролоов троугао има најмању могућу површину било које криве дате константне ширине. Ова област је

где је s константне ширине. Једна метода за извођење ове формуле површине је да се Ролоов троугао подели на унутрашњи једнакостранични троугао и три криволинијска региона између овог унутрашњег троугла и лукова који формирају Ролоов троугао, а затим се додају површине ова четири скупа. У другом екстрему, крива константне ширине која има највећу могућу површину је кружни диск, који има површину .[12]

Сви углови које ствара сваки пар лукова у угловима Ролоовог троугла су једнаки 120°. Ово је најоштрији могући угао на било ком врху било које криве константне ширине.[8] Поред тога, међу кривима константне ширине, Ролоов троугао је онај са највећим и најмањим уписаним једнакостраничним троуглом.[13] Највећи једнакостранични троугао уписан у Ролоов троугао је онај који спаја његова три угла, а најмањи је онај који спаја три средине његових страница. Подскуп Релоових троуглова који се састоје од тачака које припадају у три или више пречника је унутрашњост већег од ова два троугла; он има већу површину од скупа тачака три пречника било које друге криве константне ширине.[14]

Централно симетрични облици унутар и изван Релоовог троугла, који се користе за мерење његове асиметрије

Иако Релоов троугао има шестоструку дихедралну симетрију, исто као и једнакостранични троугао, он нема централну симетрију. Релоов троугао је најмање симетрична крива константне ширине у погледу две различите мере централне асиметрије, Ковнер-Бесикович мери (однос површине према највећем централно симетричном облику затвореном кривом) и Естермановој мери (однос површине према најмањем централно симетричном облику који обухвата криву). За Релоов троугао, два централно симетрична облика који одређују мере асиметрије су оба хексагонална, иако унутрашњи има закривљене странице.[15] Релоов троугао има пречнике који деле његову површину неравномерније од било које друге криве константне ширине. То јест, максимални однос површина са обе стране пречника, што је још једна мера асиметрије, већи је за Ролоов троугао него за друге криве константне ширине.[16]

Међу свим облицима константне ширине који избегавају све тачке целобројне решетке, онај са највећом ширином је Релоов троугао. Он има једну од својих оса симетрије паралелну са координатним оса на полуцелобројној правој. Његова ширина, отприлике 1,545, је корен полинома степена 6 са целобројним коефицијентима.[15][17][18]

Као што је могуће да круг буде окружен са шест подударних кругова који га додирују, такође је могуће распоредити седам подударних Ролоових троуглова тако да сви ступе у контакт са централним Ролоовим троуглом исте величине. Ово је највећи могући број за било коју криву константне ширине.[19]

Еквидијагонални делтоид који максимизира однос периметра и пречника, уписан у Ролоов троугао.

Међу свим четвороугловима, облик који има највећи однос свог периметра и пречника је еквидијагонални делтоид који се може уписати у Ролоов троугао.[20]

Употреба[уреди | уреди извор]

  • Ротор Ванкеловог мотора је сличан Релоовом троуглу.
  • Бургијом у облику Релоовог троугла може да се избуши рупа која је скоро савршени квадрат. Такву бургију је 1914. пројектовао и патентирао Хери Ватс (енгл. Harry Watts). Та бургија је конкавна на три места, што омогућава сечење углова квадрата и одстрањивање струготине.

Тродимензионална верзја[уреди | уреди извор]

Пресек лопти полупречника r из цента правилног тетраедра чија је страница r се зове Релоов тетраедар, али није површ са константном ширином. Али, може да се направи да буде површ са константном ширином, који се зове Мајснеров тетраедар, тако што се ивични лукови замене кривим умецима; алтернативно, ротациона површ Релоовог троугла кроз једну његову осу симетрије формира површ константне ширине, са најмањом запремином од свих ротационих површи дате константне ширине.

Референце[уреди | уреди извор]

  1. ^ Гарднер (2014) цаллс ит тхе симплест, wхиле Грубер (1983, стр. 59) цаллс ит "тхе мост ноториоус".
  2. ^ Клее, Вицтор (1971), „Схапес оф тхе футуре”, Тхе Тwо-Yеар Цоллеге Матхематицс Јоурнал, 2 (2): 14—27, ЈСТОР 3026963, дои:10.2307/3026963 .
  3. ^ Алсина, Цлауди; Нелсен, Рогер Б. (2011), Ицонс оф Матхематицс: Ан Еxплоратион оф Тwентy Кеy Имагес, Долциани Матхематицал Еxпоситионс, 45, Матхематицал Ассоциатион оф Америца, п. 155, ИСБН 978-0-88385-352-8 .
  4. ^ Моон, Ф. C. (2007), Тхе Мацхинес оф Леонардо Да Винци анд Франз Реулеауx: Кинематицс оф Мацхинес фром тхе Ренаиссанце то тхе 20тх Центурy, Хисторy оф Мецханисм анд Мацхине Сциенце, 2, Спрингер, ИСБН 978-1-4020-5598-0 .
  5. ^ а б Брyант, Јохн; Сангwин, Цхрис (2011), Хоw Роунд Ис Yоур Цирцле?: Wхере Енгинееринг анд Матхематицс Меет, Принцетон Университy Пресс, п. 190, ИСБН 978-0-691-14992-9 .
  6. ^ Ханн, Мицхаел (2014), Струцтуре анд Форм ин Десигн: Цритицал Идеас фор Цреативе Працтице, А&C Блацк, стр. 34, ИСБН 978-1-4725-8431-1 .
  7. ^ Хунгербüхлер, Норберт (1994), „А схорт елементарy прооф оф тхе Мохр-Масцхерони тхеорем”, Америцан Матхематицал Монтхлy, 101 (8): 784—787, ЦитеСеерX 10.1.1.45.9902 Слободан приступ, ЈСТОР 2974536, МР 1299166, дои:10.2307/2974536 .
  8. ^ а б Гарднер, Мартин (2014), „Цхаптер 18: Цурвес оф Цонстант Wидтх”, Кнотс анд Борромеан Рингс, Реп-Тилес, анд Еигхт Qуеенс, Тхе Неw Мартин Гарднер Матхематицал Либрарy, 4, Цамбридге Университy Пресс, стр. 223—245, ИСБН 978-0-521-75613-6 .
  9. ^ Маор, Ели; Јост, Еуген (2014), „46 Тхе Реулеауx Триангле”, Беаутифул Геометрy, Принцетон Университy Пресс, стр. 154—156, ИСБН 978-1-4008-4833-1 .
  10. ^ Реицх, Карин (2007), „Еулер'с цонтрибутион то дифферентиал геометрy анд итс рецептион”, Ур.: Брадлеy, Роберт Е.; Сандифер, Ед, Леонхард Еулер: Лифе, Wорк анд Легацy, Студиес ин тхе Хисторy анд Пхилосопхy оф Матхематицс, 5, Елсевиер, стр. 479—502, ИСБН 9780444527288, дои:10.1016/С0928-2017(07)80026-0 . Сее ин партицулар сецтион 1.4, "Орбиформс, 1781", пп. 484–485.
  11. ^ Еулер, Леонхард (1781), „Де цурвис триангуларибус”, Ацта Ацадемиае Сциентиарум Империалис Петрополитанае (на језику: латински), 1778: 3—30 . Сее ин партицулар п. 7 фор тхе дефинитион оф орбиформс.
  12. ^ Грубер, Петер M. (1983), Цонвеxитy анд итс Апплицатионс, Биркхäусер, стр. 67, ИСБН 978-3-7643-1384-5 
  13. ^ Грубер (1983, стр. 76)
  14. ^ Макеев, V. V. (2000), „Ан еxтремал пропертy оф тхе Реулеауx триангле”, Зап. Науцхн. Сем. С.-Петербург. Отдел. Мат. Инст. Стеклов. (ПОМИ), 267 (Геом. и Топол. 5): 152—155, 329, МР 1809823, С2ЦИД 116027099, дои:10.1023/А:1021287302603 .
  15. ^ а б Финцх, Стевен Р. (2003), „8.10 Реулеауx Триангле Цонстантс” (ПДФ), Матхематицал Цонстантс, Енцyцлопедиа оф Матхематицс анд итс Апплицатионс, Цамбридге Университy Пресс, стр. 513–514, ИСБН 978-0-521-81805-6 .
  16. ^ Гроемер, Х.; Wаллен, L. Ј. (2001), „А меасуре оф асyмметрy фор домаинс оф цонстант wидтх”, Беитрäге зур Алгебра унд Геометрие, 42 (2): 517—521, МР 1865537 .
  17. ^ Грубер (1983, стр. 78)
  18. ^ Саллее, Г. Т. (1969), „Тхе маxимал сет оф цонстант wидтх ин а латтице”, Пацифиц Јоурнал оф Матхематицс, 28 (3): 669—674, МР 0240724, дои:10.2140/пјм.1969.28.669 Слободан приступ .
  19. ^ Фејес Тóтх, L. (1967), „Он тхе нумбер оф еqуал дисцс тхат цан тоуцх анотхер оф тхе саме кинд”, Студиа Сциентиарум Матхематицарум Хунгарица, 2: 363—367, МР 0221388 ; Сцхопп, Ј. (1970), „Üбер дие Неwтонсцхе Захл еинер Сцхеибе константер Бреите”, Студиа Сциентиарум Матхематицарум Хунгарица (на језику: немачки), 5: 475—478, МР 0285983 .
  20. ^ Балл, D.Г. (1973), „А генералисатион оф π”, Тхе Матхематицал Газетте, 57 (402): 298—303, ЈСТОР 3616052, дои:10.2307/3616052 ; Гриффитхс, Давид; Цулпин, Давид (1975), „Пи-оптимал полyгонс”, Тхе Матхематицал Газетте, 59 (409): 165—175, ЈСТОР 3617699, дои:10.2307/3617699 .

Спољашње везе[уреди | уреди извор]

Релоов троугао на Викимедијиној остави.
Преузето из „https://sr.wikipedia.org/w/index.php?title=Reloov_trougao&oldid=24480116”