Groverov algoritam

Groverov algoritam je kvantni algoritam za pretraživanje nesortirane baze podataka sa N unosa u O(N^1/2) vremenu koristeći O(log N) memorijskog prostora (videti veliko O). Lov Grover ga je formulisao 1996.

U modelima klasičnog izračunavanja, pretraživanje i sortiranje nesortirane baze podataka ne može biti ostvareno za manje od linearnog vremena (tako da je pretraživanje elemenata član - po - član skoro optimalno). Groverov algoritam ilustruje da u kvantnom modelu pretraga može biti izvršena brže od ovoga; to jest, njegova vremenska složenost O(N^1/2) je asimptotski najbrža moguća za pretraživanje nesortirane baze podataka u kvantnom modelu. Pruža kvadratno poboljšanje, za razliku od drugih kvantnih algoritama, koji pružaju eksponencijalno poboljšanje u odnosu na njihove klasične alternative. Ipak, čak je i kvadratno poboljšanje značajno kada je N veliko.

Kao i mnogi drugi kvantni algoritmi, Groverov algoritam je probabilistički u smislu da daje tačan rezultat sa visokim procentom verovatnoće. Verovatnoća pojave greške može biti smanjena ponavljanjem algoritma. (Primer determinističkog kvantnog algoritma je Deutsch-Jozsa algorithm, koji uvek daje tačan odgovor.)

Primene

Iako se svrha Groverovog algoritma najčeće opisuje kao "pretraživanje baze podataka", moće biti tačnije opisati je kao "inverzija funkcije". Grubo rečeno, ako imamo funkciju y=f(x) koja može biti evaluirana na kvantnom računaru, ovaj algoritam nam dozvoljava da izračunamo x kada je dato y. Inverzija funkcije je povezana sa pretragom baze podataka tako što bismo mogli doći do funkcije koja daje tačnu vrednost y ako se x poklapa sa željenim unosom u bazu, i još jednu vrednost y za ostale vrednosti x.

Groverov algoritam se takođe može koristiti za određivanje središta i medijane skupa brojeva, i za rešavanje problema kolizije. Algoritam se može dalje optimizovati ako postoji više od jednog traženog unosa i traženi broj unosa je unapred poznat.

Postavka

Uzmimo nesortiranu bazu podataka sa N unosa. Algoritmu je potreban N-dimenzionalni statusni prostor H, koji može biti obezbeđen sa n=log₂ N kjubita. Uzimajući u obzir problem određivanja indeksa unosa baze podataka koji zadovoljava neki postavljeni uslov. Neka je f funkcija koja označava unose baze podataka sa 0 ili 1, gde je f(ω)=1 ako i samo ako ω zadovoljava traženi uslov. Dostupan nam je (preko kvantne crne kutije) pristup ka podproblemu u obliku linearnog operatora, U_ω, koji se ponaša kao:

$U_{\omega }|\omega \rangle =-|\omega \rangle$

$U_{\omega }|x\rangle =|x\rangle \qquad {\mbox{za svako}}\ x\neq \omega$

Naš cilj je da identifikujemo indeks $|\omega \rangle$.

Koraci algoritma

Kvantno kolo Reprezentacija Groverovog algoritma

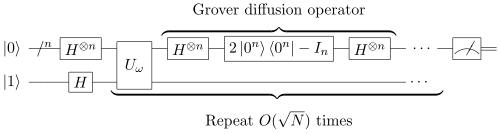
Koraci Groverovog algoritma su sledeći: Neka je $|s\rangle$ uniformna superpozicija svih stanja

$|s\rangle ={\frac {1}{\sqrt {N}}}\sum _{x=1}^{N}|x\rangle$.

Tada je operator

$U_{s}=2\left|s\right\rangle \left\langle s\right|-I$

poznat kao Groverov difuzioni operator.

Evo algoritma:

1. Inicijalizacija sistema u stanje

   $|s\rangle ={\frac {1}{\sqrt {N}}}\sum _{x=1}^{N}|x\rangle$

2. Primeniti sledeće "Groverove iteracije" r(N) puta. Funkcija r(N), koja je asimptotski O(N^½), opisana je dole.
   1. Primeniti operator $U_{\omega }$.
   2. Primeniti operator $U_{s}$.
3. Primeniti merenje Ω. Rezultati merenja će biti λ_ω sa verovatnoćom koja se približava 1 za N≫1. Iz λ_ω, se može dobiti ω.

Prva iteracija

Preliminarna observacija, paralelna sa našom definicijom

$U_{s}=2\left|s\right\rangle \left\langle s\right|-I$,

je da U_ω može biti izraženo na alternativni način:

$U_{\omega }=I-2\left|\omega \right\rangle \left\langle \omega \right|$.

Da bismo ovo dokazali dovoljno je proveriti kako se U_ω ponaša u baznim stanjima:

$(I-2|\omega \rangle \langle \omega |)|\omega \rangle =|\omega \rangle -2|\omega \rangle \langle \omega |\omega \rangle =-|\omega \rangle =U_{\omega }|\omega \rangle$.

$(I-2|\omega \rangle \langle \omega |)|x\rangle =|x\rangle -2|\omega \rangle \langle \omega |x\rangle =|x\rangle =U_{\omega }|x\rangle$ za sve $x\neq \omega$.

Sledeća izračunavanja pokazuju šta se događa u prvoj iteraciji:

$\langle \omega |s\rangle =\langle s|\omega \rangle ={\frac {1}{\sqrt {N}}}$.

$\langle s|s\rangle =N{\frac {1}{\sqrt {N}}}\cdot {\frac {1}{\sqrt {N}}}=1$.

$U_{\omega }|s\rangle =(I-2|\omega \rangle \langle \omega |)|s\rangle =|s\rangle -2|\omega \rangle \langle \omega |s\rangle =|s\rangle -{\frac {2}{\sqrt {N}}}|\omega \rangle$.

$U_{s}(|s\rangle -{\frac {2}{\sqrt {N}}}|\omega \rangle )=(2|s\rangle \langle s|-I)(|s\rangle -{\frac {2}{\sqrt {N}}}|\omega \rangle )=2|s\rangle \langle s|s\rangle -|s\rangle -{\frac {4}{\sqrt {N}}}|s\rangle \langle s|\omega \rangle +{\frac {2}{\sqrt {N}}}|\omega \rangle =$

$=2|s\rangle -|s\rangle -{\frac {4}{\sqrt {N}}}\cdot {\frac {1}{\sqrt {N}}}|s\rangle +{\frac {2}{\sqrt {N}}}|\omega \rangle =|s\rangle -{\frac {4}{N}}|s\rangle +{\frac {2}{\sqrt {N}}}|\omega \rangle ={\frac {N-4}{N}}|s\rangle +{\frac {2}{\sqrt {N}}}|\omega \rangle$.

Posle primene dva operatora ($U_{\omega }$ and $U_{s}$ ), amplituda traženog elementa je opala od $\left|\langle \omega |s\rangle \right|^{2}=1/N$ do $\left|\langle \omega |U_{s}U_{\omega }s\rangle \right|^{2}\approx 9/N$.

Opis $U_{\omega }$

Groverovom algoritmu je potreban operator "kvantnog odlučivanja" $U_{\omega }$ Koji prepoznaje rešenja traženog problema i daje im negativan znak. Da bismo održali algoritam pretrage opštim, ostavićemo unutrašnja dešavanja odlučivanja kao crnu kutiju, ali ćemo objasniti kako je znak promenjen. Odlučivanje sadrži funkciju $f$ koja vraća $f(x)=1$ ako je $|x\rangle$ rešenje traženog problema i $f(x)=0$ u suprotnom. Odlučivanje je linearni operator koji deluje na dva kjubita, indeks kjubit $|x\rangle$ i kjubit odlučivanja $|q\rangle$:

$|x\rangle |q\rangle {\overset {U_{\omega }}{\longrightarrow }}|x\rangle |q\oplus f(x)\rangle$

Kao i obično, $\oplus$ označava sabiranje po modulu 2. Operacija menja kjubit odlučivanja ako $f(x)=1$ ili ga u suprotnom ostavlja nepromenjenog. U Groverovom algoritmu želimo da promenimo znak stanja $|x\rangle$ ako obeležava rešenje. Ovo je postignuto postavljanjem kjubita pretraživanja u stanje $(|0\rangle -|1\rangle )/{\sqrt {2}}$, koje je promenjeno na $(|1\rangle -|0\rangle )/{\sqrt {2}}$ ako je $|x\rangle$ rešenje:

$|x\rangle \left(|0\rangle -|1\rangle \right)/{\sqrt {2}}{\overset {U_{\omega }}{\longrightarrow }}(-1)^{f(x)}|x\rangle \left(|0\rangle -|1\rangle \right)/{\sqrt {2}}$

Razmatramo $|x\rangle$ kao promenjeno, pošto kjubit odlučivanja nije promenjen, pa po konvenciji kjubiti odlučivanja obično nisu pomenuti u opisu Groverovog algoritma. Mada je operacija odlučivanja $U_{\omega }$ jednostavno napisana kao:

$|x\rangle {\overset {U_{\omega }}{\longrightarrow }}(-1)^{f(x)}|x\rangle$

Geometrijski dokaz korektnosti

Slika prikazuje geometrijsku reprezentaciju prve iteracije Groverovog algoritma. Vektor stanja $|s\rangle$ je rotiran ka ciljnom vektoru $|\omega \rangle$ as shown.

Posmatrajmo ravan razapetu sa $|s'\rangle$ i $|\omega \rangle$, gde je $|s'\rangle$ ket u podprostoru normalan na $|\omega \rangle$. Posmatraćemo prvu iteraciju, koja ce ponaša kao inicijalni ket $|s\rangle$. Pošto je $|\omega \rangle$ jedan od baznih vektora u $|s\rangle$ preklapanje je

$\langle s'|s\rangle ={\sqrt {\frac {N-1}{N}}}$

Na geometrijskom jeziku, ugao $\theta /2$ između $|s\rangle$ i $|s'\rangle$ je dat kao:

$\sin \theta /2={\frac {1}{\sqrt {N}}}$

Operator $U_{\omega }$ je refleksija na hiperravan ortogonalnu na $|\omega \rangle$ za vektore u ravni razapete sa $|s'\rangle$ i $|\omega \rangle$; npr. ponaša se kao refleksija preko $|s'\rangle$. Operator $U_{s}$ je refleksija kroz $|s\rangle$. Prema tome, vektor stanja ostaje u ravni razapetoj sa $|s'\rangle$ i $|\omega \rangle$ posle svake primene operatora $U_{s}$ i $U_{\omega }$, i jednostavno je proveriti da operator $U_{s}U_{\omega }$ svake Groverove iteracije rotira vektor stanja za ugao $\theta =2\arcsin {\frac {1}{\sqrt {N}}}$.

Potrebno je da stanemo kada vektor stanja prođe blizu $|\omega \rangle$; nakon ovoga, poditeracije rotiraju vektor stanja dalje od $|\omega \rangle$, umanjujući verovatnoću dobijanja tačnog odgovora. Tačna verovatnoća tačnosti odgovora je:

$\sin ^{2}\left(\left(r+{\frac {1}{2}}\right)\theta \right)$

gde jer (ceo) broj Groverovih iteracija. Najranije gde dobijamo meru blizu optimalne je prema tome $r\approx \pi {\sqrt {N}}/4$.

Algebarski dokaz korektnosti

Da bismo obavili algebarsku analizu potrebno je da otkrijemo šta se događa kada više puta primenimo $U_{s}U_{\omega }$. Prirodan način da se ovo učini je pomoću analize sopstvenih vrednosti matrice. Primetimo da tokom celokupnog izračunavanja, stanje algoritma je linearna kombinacija $s$ i $\omega$. Možemo napisati dejstvo od $U_{s}$ i $U_{\omega }$ u normalnom prostoru razapetom sa $\{|s\rangle ,|\omega \rangle \}$ kao:

$U_{s}:a|\omega \rangle +b|s\rangle \mapsto (|\omega \rangle \,|s\rangle ){\begin{pmatrix}-1&0\\2/{\sqrt {N}}&1\end{pmatrix}}{\begin{pmatrix}a\\b\end{pmatrix}}.$

$U_{\omega }:a|\omega \rangle +b|s\rangle \mapsto (|\omega \rangle \,|s\rangle ){\begin{pmatrix}-1&-2/{\sqrt {N}}\\0&1\end{pmatrix}}{\begin{pmatrix}a\\b\end{pmatrix}}.$

Tako da u bazi $\{|\omega \rangle ,|s\rangle \}$ (koja nije ni ortogonalna niti baza celokupnog prostora) dejstvo $U_{s}U_{\omega }$ primene $U_{\omega }$ praćeno sa $U_{s}$ dato je matricom

$U_{s}U_{\omega }={\begin{pmatrix}-1&0\\2/{\sqrt {N}}&1\end{pmatrix}}{\begin{pmatrix}-1&-2/{\sqrt {N}}\\0&1\end{pmatrix}}={\begin{pmatrix}1&2/{\sqrt {N}}\\-2/{\sqrt {N}}&1-4/N\end{pmatrix}}.$

Ispada da je ova matrica veoma zgodna Žordanova forma. Ako orijentišemo $t=\arcsin(1/{\sqrt {N}})$, to je

$U_{s}U_{\omega }=M{\begin{pmatrix}\exp(2it)&0\\0&\exp(-2it)\end{pmatrix}}M^{-1}$ gde je $M={\begin{pmatrix}-i&i\\\exp(it)&\exp(-it)\end{pmatrix}}.$

Ispostavlja se da je r-ti stepen matrice (U odnosu na r iteracija)

$(U_{s}U_{\omega })^{r}=M{\begin{pmatrix}\exp(2rit)&0\\0&\exp(-2rit)\end{pmatrix}}M^{-1}$

Korišćenjem ove forme možemo koristiti trigonometrijske identitete kako bismo izračunali verovatnoću posmatrajući ω nakon r iteracija pomenutih u prethodnom odeljku,

$\left|{\begin{pmatrix}\langle \omega |\omega \rangle &\langle \omega |s\rangle \end{pmatrix}}(U_{s}U_{\omega })^{r}{\begin{pmatrix}0\\1\end{pmatrix}}\right|^{2}=\sin ^{2}\left((2r+1)t\right)$.

Alternativno, neko sa pravom može pomisliti da bi vreme blizu optimalnog za razlikovanje bilo kada su uglovi 2rt and -2rt udaljeni najdalje moguće, što je u vezi sa $2rt\approx \pi /2$ or $r=\pi /4t=\pi /4\arcsin(1/{\sqrt {N}})\approx \pi {\sqrt {N}}/4$. Tada je sistem u stanju

$(|\omega \rangle \,|s\rangle )(U_{s}U_{\omega })^{r}{\begin{pmatrix}0\\1\end{pmatrix}}\approx (|\omega \rangle \,|s\rangle )M{\begin{pmatrix}i&0\\0&-i\end{pmatrix}}M^{-1}{\begin{pmatrix}0\\1\end{pmatrix}}=|w\rangle {\frac {1}{\cos(t)}}-|s\rangle {\frac {\sin(t)}{\cos(t)}}.$

Sada kratko izračunavanje pokazuje da observacija doprinosi tačnom odgovoru ω sa greškom O(1/N).

Proširenje prostora za višestruke pogotke

Ako, umesto jednog traženog unosa, postoji k unosa koji odgovaraju, isti algoritam važi, ali broj iteracija mora biti π(N/k)^1/2/4 umesto πN^1/2/4. Postoji nekoliko načina da se suočimo sa slučajem kada je k nepoznato. Na primer, jedan može primeniti Groverov algoritam nekoliko puta, sa

$\pi {\frac {N^{1/2}}{4}},\pi {\frac {(N/2)^{1/2}}{4}},\pi {\frac {(N/4)^{1/2}}{4}},\ldots$

iteracija. Za proizvoljno k, jedna od iteracija će pronaći traženi unos sa dovoljno visokom verovatnoćom. Ukupan broj iteracija je najviše

$\pi {\frac {N^{1/2}}{4}}\left(1+{\frac {1}{\sqrt {2}}}+{\frac {1}{2}}+\cdots \right)$

što je i dalje O(N^1/2). Može se pokazati da ovo može biti unapređeno. Ako je broj označenih pojmova k, gde je k nepoznato, postoji algoritam koji nalazi rešenje za ${\sqrt {N/k}}$ upita. Ova činjenica se može iskoristiti za rešavanje problema kolizija.,

Parcijalna kvantna pretraga

Modifikaciju Groverovog algoritm,a nazvanu parcijalna kvantna pretraga, opisali su Grover i Radhakrišnan 2004. godine I parcijalnoj pretrazi, nismo zainteresovani za pronalaženje tačne adrese traženog pojma, samo nekoliko prvih cifara adrese. Ekvivalentno, možemo to posmatrati kao "seckanje" prostora obuhvaćenog pretragom u blokove, i onda pitati "u kom bloku se nalazi traženi pojam?". U mnogim primenama, ovakva pretraga doprinosi dovoljno informacija ako ciljna adresa sadrži traženu informaciju. Kako bismo to pokazali, koristićemo primer dat od strane L.K. Grovera, ako imamo listu studenata uređenu po proseku ocena, možemo biti zainteresovani samo da li je student u donjem 25%, 25-50%, 50-70% ili 75-100% procentu.

Da bismo opisali parcijalnu pretragu, koristićemo bazu podataka podeljenu na $K$ blokova, od kojih je svaki veličine $b=N/K$. Očigledno, problem parcijalne pretrage je jednostavniji. Razmotrimo klasičan pristup - odaberemo nasumično jedan blok, pa zatim primenimo uobičajenu pretragu kroz ostatak blokova (na jeziku teorije skupova language, komplement). Ukoliko ne pronađemo traženi pojam, znaćemo da nije u bloku u kome smo tražili. Prosečan broj iteracija kreće se od $N/2$ do $(N-b)/2$.

Groverovom algoritmu je potrebno $\pi /4{\sqrt {N}}$ iteracija. Parcijalna pretraga će biti brža za numerički faktor koji zavisi od broja blokova $K$. Parcijalna pretraga koristi $n_{1}$ globalnih iteracija $n_{2}$ lokalnih iteracija. Globalni Groverov operator je označen sa $G_{1}$ dok je lokalni Groverov operator označen sa $G_{2}$.

Globalni Groverov operator deluje na blokove. Specijalno, dat je kao:

1. Primeniti $j_{1}$ standardnih Groverovih iteracija na celokupnu bazu.
2. Primeniti $j_{2}$ lokalnih Groverovih iteracija. Lokalna Groverova iteracija je direktna suma Groverovih iteracija i svakog bloka.
3. Primeniti jednu standatdnu Groverovu iteraciju

Optimalne vrednosti $j_{1}$ i $j_{2}$ su razmotrene u članku Grovera i Radhakrišnana. Neko se može zapitati šta se dešava ako se primeni uzastopna parcijalna pretraga na različitim nivoima "rezolucije". Ova ideja je detaljno proučena od strane Korepina and Ksua, koji su je nazvali kvantno binarno stablo pretrage. Dokazali su da da nije brža u odnosu na primenu jedne parcijalne pretrage.

Optimalnost

Poznato je da je Groverov algoritam optimalan. Što će reći, bilo koji algoritam koji pristupa bazi podataka korišćenjem samo operatora U_ω mora primeniti U_ω najmanje onoliko puta koliko i Groverov algoritam. Ovaj rezultat je bitan za razumevanje ograničenja kvantnog izračunavanja. Da je problem Groverove pretrage rešiv za log^c N primenom U_ω, iz toga bi sledilo da je klasa NP sadržana u BQP, svođenjem problema iz NP na probleme tipa Groverove pretrage. Optimalnost Groverovog algoritma nalaže (ali ne dokazuje) da klasa NP nije sadržana u BQP.

Broj iteracija za k pronađenih pogodaka, π(N/k)^1/2/4, je takođe optimalan.

Literatura

• Grover, Lov K. (1996). „A fast quantum mechanical algorithm for database search”. Bibcode:1996quant.ph..5043G. arXiv:quant-ph/9605043 . 
• Grover, Lov K. (2001). „From Schrödinger's equation to the quantum search algorithm”. Pramana. 69 (7): 769—777. Bibcode:2001Prama..56..333G. S2CID 9505022. arXiv:quant-ph/0109116 . doi:10.1007/s12043-001-0128-3. 
• Nielsen, M.A. and Chuang, I.L. Quantum computation and quantum information. Cambridge University Press, 2000. Chapter 6.
• What's a Quantum Phone Book?, Lov Grover, Lucent Technologies
• Lavor, C.; Manssur, L. R. U.; Portugal, R. (2003). „Grover's Algorithm: Quantum Database Search”. Bibcode:2003quant.ph..1079L. arXiv:quant-ph/0301079 . 
• Grover's algorithm on arxiv.org

Spoljašnje veze

• Grover's Algorithm simulation and circuit diagram.
• Grover’s Quantum Search Algorithm Архивирано на сајту Wayback Machine (17. новембар 2020) animated explanation.
• Simulation and circuit diagram with cats