Активациона функција

У вештачким неуронским мрежама, активациона функција чвора дефинише излаз тог чвора на основу улаза или скупа улаза. Стандардно коло компјутерског чипа може се гледати као дигитална мрежа активационих функција које могу имати вредност „укључено” (1) или „искључено” (0), у зависности од улаза. Ово је слично понашању линеарног перцептрона у неуронским мрежама. Међутим, само нелинеарне активационе функције дозвољавају таквим мрежама да израчунају нетривијалне проблеме користећи само мали број чворова.^[1] У вештачким неуронским мрежама, ова функција се назива и функција преноса.

Функције[уреди | уреди извор]

У биолошки инспирисаним неуронским мрежама, активациона функција је обично апстракција која представља стопу акционог потенцијала који се појављује у ћелији. У својој најједноставнијој форми, ова функција је бинарна — тј. или се неурон активира или не. Функција изгледа као $\phi (v_{i})=U(v_{i})$ , гдје је $U$ Хевисајдова одскочна функција. У овом случају многи неурони се морају користити у рачунању изван линеарног раздвајања категорија.

Линија позитивног нагиба може се користити да би се одразило повећање стопе активирања која се јавља како се улазна струја повећава. Таква функција би била у форми $\phi (v_{i})=\mu v_{i}$ , где је $\mu$ нагиб. Ова активациона функција је линеарна и стога има исте проблеме као и бинарна функција. Поред тога, мреже конструисане коришћењем овог модела имају нестабилну конвергенцију зато што неуронски улази по фаворизованим путевима имају тенденцију да се повећају без везивања, јер ова функција није нормализована.

Сви наведени проблеми могу се обрадити коришћењем нормализоване сигмоидне активационе функције. Један реалан модел остаје на нули све док не прими улазну струју. У том тренутку, стопа активације се прво брзо повећава, али се постепено приближава асимптоти са стопом од 100%. Математички, ово изгледа као $\phi (v_{i})=U(v_{i})\tanh(v_{i})$ , где се хипероболичка тангентна функција може заменити било којом сигмоидном функцијом. Ово понашање се реално рефлектује у неурону, јер неурони физички не могу да се активирају брже од одређене стопе. Међутим, овај модел се сусреће са проблемима у рачунарским мрежама, јер није диференцијабилан, што је захтев за израчунавање бекпропагације.

Коначни модел, који се користи у вишеслојним перцептронима, је сигмоидна активациона функција у облику хиперболичног тангенса. Обично се користе два облика ове функције: $\phi (v_{i})=\tanh(v_{i})$ , чији је распон нормализован од -1 до 1 и $\phi (v_{i})=(1+\exp(-v_{i}))^{-1}$ , који је вертикално транслиран како би био нормализован од 0 до 1. Овај последњи модел често се сматра биолошки реалнијим, али има теоријске и експерименталне потешкоће са одређеним типовима рачунарских проблема.

Поређење активационих функција[уреди | уреди извор]

Активационе функције треба да имају нека пожељна својства, међу којима су:

Нелинеарност — Када је активациона функција нелинеаерна, онда се може доказати да је двослојна неуронска мрежа универзални апроксиматор функције.^[2]
Интервал — Када је интервал активационе функције коначан, методе учења засноване на градијенту имају тенденцију да буду стабилније. Када је интервал бесконачан, учење је генерално ефикасније.
Непрекидна диференцијабилност — Ово својство је пожељно (ReLU није непрекидно диференцијабилан и има неке проблеме са оптимизацијом заснованом на градијенту) за омогућавање метода оптимизације заснованих на градијенту. Активациона бинарна одскочна функција није диференцијабилна у нули, а извод јој је 0 за све остале вредности, тако да методе засноване на градијенту немају напретка са овом функцијом.^[3]
Монотоност — Када је активациона функција монотона, површина грешке која је повезана са једнослојним моделом гарантовано је конвексна.^[4]
Глатке функције са монотоним изводом — За ове функције показало се да у неким случајевима боље генерализују.
Апроксимација идентитета приближно оригиналу — Када активационе функције имају ово својство, неуронска мрежа ће ефикасно учити када се њене тежине иницијализују на мале случајне вредности. Када активациона функција не апроксимира идентитет приближан оригиналу, приликом иницијализације тежина мора се обратити посебна пажња.^[5] У табели испод, активацион ефункције где је $f(0)=9$ и $f'(0)=1$ и где је $f'$ непрекидно у 0, означене су да имају ово својство.

Следећа табела пореди својства неколико активационих функција:

Назив	Једначина	Извод (по x)	Интервал	Ред непрекидности	Монотона	Монотон извод	Апроксимира идентитет приближно оригиналу
Функција идентитета	$f(x)=x$	$f'(x)=1$	$(-\infty ,\infty )$	$C^{\infty }$	Да	Да	Да
Бинарна одскочна функција	$f(x)={\begin{cases}0&{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}$	$f'(x)={\begin{cases}0&{\text{for }}x\neq 0\\?&{\text{for }}x=0\end{cases}}$	$\{0,1\}$	$C^{-1}$	Да	Не	Не
Сигмоидна функција	$f(x)=\sigma (x)={\frac {1}{1+e^{-x}}}$ ^[1]	$f'(x)=f(x)(1-f(x))$	$(0,1)$	$C^{\infty }$	Да	Не	Не
Хиперболички тангенс	$f(x)=\tanh(x)={\frac {(e^{x}-e^{-x})}{(e^{x}+e^{-x})}}$	$f'(x)=1-f(x)^{2}$	$(-1,1)$	$C^{\infty }$	Да	Не	Да
Инверзни тангенс	$f(x)=\tan ^{-1}(x)$	$f'(x)={\frac {1}{x^{2}+1}}$	$\left(-{\frac {\pi }{2}},{\frac {\pi }{2}}\right)$	$C^{\infty }$	Да	Не	Да
Инверзни хиперболички синус	$f(x)=\sinh ^{-1}(x)=\ln \left(x+{\sqrt {x^{2}+1}}\right)$	$f'(x)={\frac {1}{\sqrt {x^{2}+1}}}$	$(-\infty ,\infty )$	$C^{\infty }$	Да	Не	Да
ElliotSig^[6]^[7]^[8] Softsign^[9]^[10]	$f(x)={\frac {x}{1+\|x\|}}$	$f'(x)={\frac {1}{(1+\|x\|)^{2}}}$	$(-1,1)$	$C^{1}$	Да	Не	Да
ISRU^[11]	$f(x)={\frac {x}{\sqrt {1+\alpha x^{2}}}}$	$f'(x)=\left({\frac {1}{\sqrt {1+\alpha x^{2}}}}\right)^{3}$	$\left(-{\frac {1}{\sqrt {\alpha }}},{\frac {1}{\sqrt {\alpha }}}\right)$	$C^{\infty }$	Да	Не	Да
ISRLU^[11]	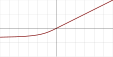$f(x)={\begin{cases}{\frac {x}{\sqrt {1+\alpha x^{2}}}}&{\text{for }}x<0\\x&{\text{for }}x\geq 0\end{cases}}$	$f'(x)={\begin{cases}\left({\frac {1}{\sqrt {1+\alpha x^{2}}}}\right)^{3}&{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}$	$\left(-{\frac {1}{\sqrt {\alpha }}},\infty \right)$	$C^{2}$	Да	Да	Да
SQNL^[8]	$f(x)={\begin{cases}1&:x>2.0\\x-{\frac {x^{2}}{4}}&:0\leq x\leq 2.0\\x+{\frac {x^{2}}{4}}&:-2.0\leq x<0\\*1&:x<-2.0\end{cases}}$	$f'(x)=1\mp {\frac {x}{2}}$	$(-1,1)$	$C^{2}$	Да	Не	Да
ReLU^[12]	$f(x)={\begin{cases}0&{\text{for }}x<0\\x&{\text{for }}x\geq 0\end{cases}}$	$f'(x)={\begin{cases}0&{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}$	$[0,\infty )$	$C^{0}$	Да	Да	Не
BReLU^[13]	$f(x_{i})={\begin{cases}ReLU(x_{i})&{\text{if }}i{\bmod {2}}=0\\-ReLU(-x_{i})&{\text{if }}i{\bmod {2}}\neq 0\end{cases}}$	$f'(x_{i})={\begin{cases}ReLU'(x_{i})&{\text{if }}i{\bmod {2}}=0\\-ReLU'(-x_{i})&{\text{if }}i{\bmod {2}}\neq 0\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$	Да	Да	Не
Leaky ReLU^[14]	$f(x)={\begin{cases}0.01x&{\text{for }}x<0\\x&{\text{for }}x\geq 0\end{cases}}$	$f'(x)={\begin{cases}0.01&{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$	Да	Да	Не
PReLU^[15]	$f(\alpha ,x)={\begin{cases}\alpha x&{\text{for }}x<0\\x&{\text{for }}x\geq 0\end{cases}}$	$f'(\alpha ,x)={\begin{cases}\alpha &{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$	Да akko $\alpha \geq 0$	Да	Да akko $\alpha =1$
RReLU^[16]	$f(\alpha ,x)={\begin{cases}\alpha x&{\text{for }}x<0\\x&{\text{for }}x\geq 0\end{cases}}$ ^[2]	$f'(\alpha ,x)={\begin{cases}\alpha &{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$	Да	Да	Не
ELU^[17]	$f(\alpha ,x)={\begin{cases}\alpha (e^{x}-1)&{\text{for }}x\leq 0\\x&{\text{for }}x>0\end{cases}}$	$f'(\alpha ,x)={\begin{cases}f(\alpha ,x)+\alpha &{\text{for }}x\leq 0\\1&{\text{for }}x>0\end{cases}}$	$(-\alpha ,\infty )$	${\begin{cases}C_{1}&{\text{за }}\alpha =1\\C_{0}&{\text{иначе }}\end{cases}}$	Да akko $\alpha \geq 0$	Да akko $0\leq \alpha \leq 1$	Да akko $\alpha =1$
SELU^[18]	$f(\alpha ,x)=\lambda {\begin{cases}\alpha (e^{x}-1)&{\text{for }}x<0\\x&{\text{for }}x\geq 0\end{cases}}$ са $\lambda =1.0507$ и $\alpha =1.67326$	$f'(\alpha ,x)=\lambda {\begin{cases}\alpha (e^{x})&{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}$	$(-\lambda \alpha ,\infty )$	$C^{0}$	Да	Не	Не
SReLU^[19]	$f_{t_{l},a_{l},t_{r},a_{r}}(x)={\begin{cases}t_{l}+a_{l}(x-t_{l})&{\text{for }}x\leq t_{l}\\x&{\text{for }}t_{l}<x<t_{r}\\t_{r}+a_{r}(x-t_{r})&{\text{for }}x\geq t_{r}\end{cases}}$ $t_{l},a_{l},t_{r},a_{r}$ су параметри.	$f'_{t_{l},a_{l},t_{r},a_{r}}(x)={\begin{cases}a_{l}&{\text{for }}x\leq t_{l}\\1&{\text{for }}t_{l}<x<t_{r}\\a_{r}&{\text{for }}x\geq t_{r}\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$	Не	Не	Не
APL^[20]	$f(x)=\max(0,x)+\sum _{s=1}^{S}a_{i}^{s}\max(0,-x+b_{i}^{s})$	$f'(x)=H(x)-\sum _{s=1}^{S}a_{i}^{s}H(-x+b_{i}^{s})$ ^[3]	$(-\infty ,\infty )$	$C^{0}$	Не	Не	Не
SoftPlus^[21]	$f(x)=\ln(1+e^{x})$	$f'(x)={\frac {1}{1+e^{-x}}}$	$(0,\infty )$	$C^{\infty }$	Да	Да	Не
Савијена функција идентиета	$f(x)={\frac {{\sqrt {x^{2}+1}}-1}{2}}+x$	$f'(x)={\frac {x}{2{\sqrt {x^{2}+1}}}}+1$	$(-\infty ,\infty )$	$C^{\infty }$	Да	Да	Да
SiLU^[22] (SiL^[23] или Swish-1^[24])	$f(x)=x\cdot \sigma (x)$ ^[4]	$f'(x)=f(x)+\sigma (x)(1-f(x))$ ^[5]	$[\approx -0.28,\infty )$	$C^{\infty }$	Не	Не	Апроксимира идентитет/2
Блага експоненцијална функција^[25]	$f(\alpha ,x)={\begin{cases}-{\frac {\ln(1-\alpha (x+\alpha ))}{\alpha }}&{\text{for }}\alpha <0\\x&{\text{for }}\alpha =0\\{\frac {e^{\alpha x}-1}{\alpha }}+\alpha &{\text{for }}\alpha >0\end{cases}}$	$f'(\alpha ,x)={\begin{cases}{\frac {1}{1-\alpha (\alpha +x)}}&{\text{for }}\alpha <0\\e^{\alpha x}&{\text{for }}\alpha \geq 0\end{cases}}$	$(-\infty ,\infty )$	$C^{\infty }$	Да	Да	Да akko $\alpha =0$
Soft Clipping^[26]	$f(\alpha ,x)={\frac {1}{\alpha }}\log {\frac {1+e^{\alpha x}}{1+e^{\alpha (x-1)}}}$	$f'(\alpha ,x)={\frac {1}{2}}\sinh \left({\frac {p}{2}}\right){\text{sech}}\left({\frac {px}{2}}\right){\text{sech}}\left({\frac {p}{2}}(1-x)\right)$	$(0,1)$	$C^{\infty }$	Да	Не	Не
Синусоида^[27]	$f(x)=\sin(x)$	$f'(x)=\cos(x)$	$[-1,1]$	$C^{\infty }$	Не	Не	Да
Sinc	$f(x)={\begin{cases}1&{\text{for }}x=0\\{\frac {\sin(x)}{x}}&{\text{for }}x\neq 0\end{cases}}$	$f'(x)={\begin{cases}0&{\text{for }}x=0\\{\frac {\cos(x)}{x}}-{\frac {\sin(x)}{x^{2}}}&{\text{for }}x\neq 0\end{cases}}$	$[\approx -.217234,1]$	$C^{\infty }$	Не	Не	Не
Гаусова функција	$f(x)=e^{-x^{2}}$	$f'(x)=-2xe^{-x^{2}}$	$(0,1]$	$C^{\infty }$	Не	Не	Не

^ Овде,

H

је Хевисајдова функција.

^

α

је стохастичка променљива изведена из униформне расподеле времена учења и фиксирана је на очекивану вредност расподеле времена тестирања.

^ ^ ^ Овде,

\sigma

је логистичка функција.

Следећа табела садржи активационе функције које нису функције једног сложеног $x$ из претходног слоја или слојева:

Назив	Једначина	Изводи	Интервал	Ред непрекидности
Softmax	$f_{i}({\vec {x}})={\frac {e^{x_{i}}}{\sum _{j=1}^{J}e^{x_{j}}}}$ for $i$ = 1, …, $J$	${\frac {\partial f_{i}({\vec {x}})}{\partial x_{j}}}=f_{i}({\vec {x}})(\delta _{ij}-f_{j}({\vec {x}}))$ ^[6]	$(0,1)$	$C^{\infty }$
Maxout^[28]	$f({\vec {x}})=\max _{i}x_{i}$	${\frac {\partial f}{\partial x_{j}}}={\begin{cases}1&{\text{for }}j={\underset {i}{\operatorname {argmax} }}\,x_{i}\\0&{\text{for }}j\neq {\underset {i}{\operatorname {argmax} }}\,x_{i}\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$

Референце[уреди | уреди извор]

^ Hinkelmann, Knut. „Neural Networks,” (PDF). University of Applied Science Northwestern Switzerland. стр. 7. Архивирано из оригинала (PDF) 06. 10. 2018. г. Невалидан унос |dead-url=dead (помоћ)
^ Mathematics of Control, Signals, and Systems: MCSS. (на језику: енглески). Springer International. 2006.
^ Snyman, Jan (2005). Practical Mathematical Optimization: An Introduction to Basic Optimization Theory and Classical and New Gradient-Based Algorithms (на језику: енглески). Springer Science & Business Media. ISBN 9780387243481.
^ Wu, Huaiqin (9. 9. 2009). „Global stability analysis of a general class of discontinuous neural networks with linear growth activation functions”. Information Sciences. 179 (19): 3432—3441. ISSN 0020-0255. doi:10.1016/j.ins.2009.06.006.
^ Abbott, L. F.; Sussillo, David (19. 12. 2014). „Random Walk Initialization for Training Very Deep Feedforward Networks” (на језику: енглески).
^ Elliot, David L. (1993), „A better activation function for artificial neural networks”, ISR Technical Report TR 93-8, University of Maryland, College Park, MD 20742., CiteSeerX 10.1.1.46.7204 
^ „elliotsig, Elliot symmetric sigmoid transfer function”, command introduced in Matlab R2012b, Matlab Documentation, MathWorks.
^ ^а ^б Wuraola, Adedamola; Patel, Nitish (2018), „SQNL:A New Computationally Efficient Activation Function”, 2018 International Joint Conference on Neural Networks (IJCNN), Rio Rio de Janeiro, Brazil: IEEE, стр. 1—7
^ Bergstra, James; Desjardins, Guillaume; Lamblin, Pascal; Bengio, Yoshua (2009). „Quadratic polynomials learn better image features". Technical Report 1337”. Département d’Informatique et de Recherche Opérationnelle, Université de Montréal. Архивирано из оригинала 25. 9. 2018. г.
^ Glorot, Xavier; Bengio, Yoshua (2010), „Understanding the difficulty of training deep feedforward neural networks” (PDF), International Conference on Artificial Intelligence and Statistics (AISTATS'10), Society for Artificial Intelligence and Statistics, Архивирано из оригинала (PDF) 01. 04. 2017. г.
^ ^а ^б Carlile, Brad; Delamarter, Guy; Kinney, Paul; Marti, Akiko; Whitney, Brian (9. 11. 2017). „Improving Deep Learning by Inverse Square Root Linear Units (ISRLUs)”. arXiv:1710.09967  [cs.LG].
^ Nair, Vinod; Hinton, Geoffrey E. (2010), „Rectified Linear Units Improve Restricted Boltzmann Machines”, 27th International Conference on International Conference on Machine Learning, ICML'10, USA: Omnipress, стр. 807—814, ISBN 9781605589077
^ Eidnes, Lars; Nøkland, Arild (2018). „Shifting Mean Activation Towards Zero with Bipolar Activation Functions”. International Conference on Learning Representations (ICLR) Workshop. arXiv:1709.04054 .
^ Maas, Andrew L.; Hannun, Awni Y.; Ng, Andrew Y. (јун 2013). „Rectifier nonlinearities improve neural network acoustic models” (PDF). Proc. ICML. 30 (1). Архивирано из оригинала (PDF) 03. 01. 2017. г. Приступљено 2. 1. 2017.
^ He, Kaiming; Zhang, Xiangyu; Ren, Shaoqing; Sun, Jian (6. 2. 2015). „Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification”. arXiv:1502.01852  [cs.CV].
^ Xu, Bing; Wang, Naiyan; Chen, Tianqi; Li, Mu (4. 5. 2015). „Empirical Evaluation of Rectified Activations in Convolutional Network”. arXiv:1505.00853  [cs.LG].
^ Clevert, Djork-Arné; Unterthiner, Thomas; Hochreiter, Sepp (23. 11. 2015). „Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs)”. arXiv:1511.07289  [cs.LG].
^ Klambauer, Günter; Unterthiner, Thomas; Mayr, Andreas; Hochreiter, Sepp (8. 6. 2017). „Self-Normalizing Neural Networks”. Advances in Neural Information Processing Systems. 30 (2017). Bibcode:2017arXiv170602515K. arXiv:1706.02515 .
^ Jin, Xiaojie; Xu, Chunyan; Feng, Jiashi; Wei, Yunchao; Xiong, Junjun; Yan, Shuicheng (22. 12. 2015). „Deep Learning with S-shaped Rectified Linear Activation Units”. arXiv:1512.07030  [cs.CV].
^ Agostinelli, Forest; Hoffman, Matthew; Sadowski, Peter; Baldi, Pierre (21. 12. 2014). „Learning Activation Functions to Improve Deep Neural Networks”. arXiv:1412.6830  [cs.NE].
^ Glorot, Xavier; Bordes, Antoine; Bengio, Yoshua (2011). „Deep sparse rectifier neural networks” (PDF). International Conference on Artificial Intelligence and Statistics.
^ Hendrycks, Dan; Gimpel, Kevin (2016). „Gaussian Error Linear Units (GELUs)”. arXiv:1606.08415  [cs.LG].
^ Elfwing, Stefan; Uchibe, Eiji; Doya, Kenji (2017). „Sigmoid-Weighted Linear Units for Neural Network Function Approximation in Reinforcement Learning”. arXiv:1702.03118  [cs.LG].
^ Ramachandran, Prajit; Zoph, Barret; Le, Quoc V (2017). „Searching for Activation Functions”. arXiv:1710.05941  [cs.NE].
^ Godfrey, Luke B.; Gashler, Michael S. (3. 2. 2016). „A continuum among logarithmic, linear, and exponential functions, and its potential to improve generalization in neural networks”. 7th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management: KDIR. 1602: 481—486. Bibcode:2016arXiv160201321G. arXiv:1602.01321 .
^ Klimek, Matthew D.; Perelstein, Maxim (26. 10. 2018). „Neural Network-Based Approach to Phase Space Integration”. arXiv:1810.11509  [hep-ph].
^ Gashler, Michael S.; Ashmore, Stephen C. (9. 5. 2014). „Training Deep Fourier Neural Networks To Fit Time-Series Data”. arXiv:1405.2262  [cs.NE].
^ Goodfellow, Ian J.; Warde-Farley, David; Mirza, Mehdi; Courville, Aaron; Bengio, Yoshua (2013). „Maxout Networks”. JMLR Workshop and Conference Proceedings. 28 (3): 1319—1327. Bibcode:2013arXiv1302.4389G. arXiv:1302.4389 .

[1] Hinkelmann, Knut. „Neural Networks,” (PDF). University of Applied Science Northwestern Switzerland. стр. 7. Архивирано из оригинала (PDF) 06. 10. 2018. г. Невалидан унос |dead-url=dead (помоћ)

[2] Mathematics of Control, Signals, and Systems: MCSS. (на језику: енглески). Springer International. 2006.

[3] Snyman, Jan (2005). Practical Mathematical Optimization: An Introduction to Basic Optimization Theory and Classical and New Gradient-Based Algorithms (на језику: енглески). Springer Science & Business Media. ISBN 9780387243481.

[4] Wu, Huaiqin (9. 9. 2009). „Global stability analysis of a general class of discontinuous neural networks with linear growth activation functions”. Information Sciences. 179 (19): 3432—3441. ISSN 0020-0255. doi:10.1016/j.ins.2009.06.006.

[5] Abbott, L. F.; Sussillo, David (19. 12. 2014). „Random Walk Initialization for Training Very Deep Feedforward Networks” (на језику: енглески).

[6] Elliot, David L. (1993), „A better activation function for artificial neural networks”, ISR Technical Report TR 93-8, University of Maryland, College Park, MD 20742., CiteSeerX 10.1.1.46.7204 

[7] „elliotsig, Elliot symmetric sigmoid transfer function”, command introduced in Matlab R2012b, Matlab Documentation, MathWorks.

[sqln-8] а ^б Wuraola, Adedamola; Patel, Nitish (2018), „SQNL:A New Computationally Efficient Activation Function”, 2018 International Joint Conference on Neural Networks (IJCNN), Rio Rio de Janeiro, Brazil: IEEE, стр. 1—7

[9] Bergstra, James; Desjardins, Guillaume; Lamblin, Pascal; Bengio, Yoshua (2009). „Quadratic polynomials learn better image features". Technical Report 1337”. Département d’Informatique et de Recherche Opérationnelle, Université de Montréal. Архивирано из оригинала 25. 9. 2018. г.

[10] Glorot, Xavier; Bengio, Yoshua (2010), „Understanding the difficulty of training deep feedforward neural networks” (PDF), International Conference on Artificial Intelligence and Statistics (AISTATS'10), Society for Artificial Intelligence and Statistics, Архивирано из оригинала (PDF) 01. 04. 2017. г.

[isrlu-11] а ^б Carlile, Brad; Delamarter, Guy; Kinney, Paul; Marti, Akiko; Whitney, Brian (9. 11. 2017). „Improving Deep Learning by Inverse Square Root Linear Units (ISRLUs)”. arXiv:1710.09967  [cs.LG].

[12] Nair, Vinod; Hinton, Geoffrey E. (2010), „Rectified Linear Units Improve Restricted Boltzmann Machines”, 27th International Conference on International Conference on Machine Learning, ICML'10, USA: Omnipress, стр. 807—814, ISBN 9781605589077

[13] Eidnes, Lars; Nøkland, Arild (2018). „Shifting Mean Activation Towards Zero with Bipolar Activation Functions”. International Conference on Learning Representations (ICLR) Workshop. arXiv:1709.04054 .

[14] Maas, Andrew L.; Hannun, Awni Y.; Ng, Andrew Y. (јун 2013). „Rectifier nonlinearities improve neural network acoustic models” (PDF). Proc. ICML. 30 (1). Архивирано из оригинала (PDF) 03. 01. 2017. г. Приступљено 2. 1. 2017.

[15] He, Kaiming; Zhang, Xiangyu; Ren, Shaoqing; Sun, Jian (6. 2. 2015). „Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification”. arXiv:1502.01852  [cs.CV].

[16] Xu, Bing; Wang, Naiyan; Chen, Tianqi; Li, Mu (4. 5. 2015). „Empirical Evaluation of Rectified Activations in Convolutional Network”. arXiv:1505.00853  [cs.LG].

[17] Clevert, Djork-Arné; Unterthiner, Thomas; Hochreiter, Sepp (23. 11. 2015). „Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs)”. arXiv:1511.07289  [cs.LG].

[18] Klambauer, Günter; Unterthiner, Thomas; Mayr, Andreas; Hochreiter, Sepp (8. 6. 2017). „Self-Normalizing Neural Networks”. Advances in Neural Information Processing Systems. 30 (2017). Bibcode:2017arXiv170602515K. arXiv:1706.02515 .

[19] Jin, Xiaojie; Xu, Chunyan; Feng, Jiashi; Wei, Yunchao; Xiong, Junjun; Yan, Shuicheng (22. 12. 2015). „Deep Learning with S-shaped Rectified Linear Activation Units”. arXiv:1512.07030  [cs.CV].

[20] Agostinelli, Forest; Hoffman, Matthew; Sadowski, Peter; Baldi, Pierre (21. 12. 2014). „Learning Activation Functions to Improve Deep Neural Networks”. arXiv:1412.6830  [cs.NE].

[21] Glorot, Xavier; Bordes, Antoine; Bengio, Yoshua (2011). „Deep sparse rectifier neural networks” (PDF). International Conference on Artificial Intelligence and Statistics.

[22] Hendrycks, Dan; Gimpel, Kevin (2016). „Gaussian Error Linear Units (GELUs)”. arXiv:1606.08415  [cs.LG].

[23] Elfwing, Stefan; Uchibe, Eiji; Doya, Kenji (2017). „Sigmoid-Weighted Linear Units for Neural Network Function Approximation in Reinforcement Learning”. arXiv:1702.03118  [cs.LG].

[24] Ramachandran, Prajit; Zoph, Barret; Le, Quoc V (2017). „Searching for Activation Functions”. arXiv:1710.05941  [cs.NE].

[25] Godfrey, Luke B.; Gashler, Michael S. (3. 2. 2016). „A continuum among logarithmic, linear, and exponential functions, and its potential to improve generalization in neural networks”. 7th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management: KDIR. 1602: 481—486. Bibcode:2016arXiv160201321G. arXiv:1602.01321 .

[26] Klimek, Matthew D.; Perelstein, Maxim (26. 10. 2018). „Neural Network-Based Approach to Phase Space Integration”. arXiv:1810.11509  [hep-ph].

[27] Gashler, Michael S.; Ashmore, Stephen C. (9. 5. 2014). „Training Deep Fourier Neural Networks To Fit Time-Series Data”. arXiv:1405.2262  [cs.NE].

[28] Goodfellow, Ian J.; Warde-Farley, David; Mirza, Mehdi; Courville, Aaron; Bengio, Yoshua (2013). „Maxout Networks”. JMLR Workshop and Conference Proceedings. 28 (3): 1319—1327. Bibcode:2013arXiv1302.4389G. arXiv:1302.4389 .

[1]

[2]

[3]

[4]

[5]

[1]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[2]

[17]

[18]

[19]

[20]

[3]

[21]

[22]

[23]

[24]

[4]

[5]

[25]

[26]

[27]

[6]

[28]