Статика флуида

Статика флуида се бави флуидима у стању мировања и део је механике флуида.[3][4] Флуид је у стању мировања ако постоји координатни систем у којем је брзина флуидних делића у свакој тачки флуида једнака нули.[5] Флуид се при мировању налази у „савршеном“ стању јер његова вискозност не долази до изражаја. Наиме, на основу Хипотезе о великој покретљивости (Хипотеза о великој и лакој деформабилности) последица молекуларне микроструктуре течности и гасова је лака покретљивост (течљивост) тако да и врло мале силе изазивају велике деформације. Директне последице ове хипотезе су следеће:
- Смицајни (тангенцијални) напони, односно трење се не јавља у флуиду који мирује. Међутим, иако струјање флуида неминовно изазива, тј. генерише силу трења, у неким случајевима струјања флуида се силе трења могу занемарити у односу на инерцијалне силе, тако да се у тим случајевима може говорити о моделу невискозног флуида (савршени флуид).
- Из горњег својства долази се до следеће последице исте хипотезе: Међудејство флуида са различитих страна неке површи се остварује искључиво у правцу нормале на површ. Како се напони истезања не могу јавити у флуиду, остаје да се нормални напони своде на притисак.[/br]
У статици флуида важе два основна закона:
Основна једначина статике флуида је Ојлерова једначина:[6][7][8]
где је :
- ρ - густина флуида (густина масе)[kg/m³],
- - густина масене силе тј. масена сила по јединици масе [N/m³],
- - градијент притиска, при чему је векторски оператор набла.
Задатак статике флуида састоји се у томе да се из Ојлерове једначине статике флуида уз познату густину масене силе и познату густину флуида (густина масе) израчуна расподела притиска. Ојлерова једначина изражава следећу законитост: у мирујућем флуиду највећа промена притиска (grad p) је у смеру масене силе . Градијент притиска је вектор нормалан на изобарску површ. Изобарске површи су површи једнаког притиска.
О облику површина p=const[уреди | уреди извор]
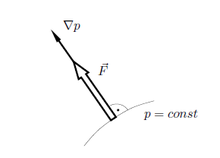
Из Ојлерове једначине у векторском облику произилази следеће: Скаларно поље притисака се формира тако да површи константног притиска (изобарске површи) у свакој тачки за нормалу имају задато поље масених сила . Вектори и су међусобно колинерани вектори.
Да ли ће изобарске површи бити криве или равне зависи од природе (карактера) масених сила. Ако је поље сила хомогено (), површи морају бити равне. За случај нехомогеног поља масених сила изобарске површи су криве површи.
Стање напона[уреди | уреди извор]
, где је: - вектор напона у произвољној тачки струјног простора
- У флуиду који мирује не постоји трење.
- Притисак p при мировању флуида се означава као статички притисак.
- Стање напона дефинисано је скаларним пољем притиска . Притисак је скалар.
Притисак у флуидима при мировању[уреди | уреди извор]
Због фундаменталне природе флуида, флуид не може остати у мировању у присуству смицања. Међутим, флуиди могу да врше притисак нормално на контактну површину. Ако се тачка у флуиду сматра бесконачно малом коцком, онда из принципа равнотеже следи да притисак на свакој страни те јединице мора бити једнак. Да то није био случај, течност би се кретала у правцу резултирајуће силе. Стога, притисак на флуид у мировању је изотропан; тј., он делује са једнаком магнитудом у свим правцима. Ова карактеристика омогућава флуидима да преносе силу кроз дужину цеви; тј., сила примењена на флуид у цеви се преноси, преко флуида, до другог краја цеви. Овај принцип је првобитно формулисао, у нешто ширем облику Блез Паскал, и стога се назива Паскалов закон.[9][10][11]
Хидростатички притисак[уреди | уреди извор]
У флуиду у мировању, сва фрикциона и инерцијална напрезања нестају и стање напрезања система се назива хидростатичким. Када се ово стање од V = 0 примени на Навје–Стоксове једначине, градијент притиска постаје само функција масених сила. За баротропни флуид у конзервативном пољу сила као што је поље гравитационе силе, притисак који врши флуид у равнотежи постаје функција силе која врши гравитација.
Хидростатички притисак се може одредити из анализе контролне запремине инфинитезимално мале коцке флуида. Пошто је притисак дефинисан као сила која делује на тестну површину (p = F/A, где је p: притисак, F: сила нормална на површину A, A: површина), а једина сила која делује на било коју такву малу коцку флуида је тежина колоне флуида изнад ње, хидростатски притисак се може израчунати према следећој формули:
где је:
- p - хидростатички притисак (Pa),
- ρ - густина флуида (kg/m3),
- g - гравитационо убрзање (m/s2),
- A - тестна површина (m²),
- z - висина (паралелна правцу гравитације) тестне површине (m),
- z0 - висина нулте референтне тачке притиска (m).
Референце[уреди | уреди извор]
- ^ Chambers, Ephraim (1728). Cyclopædia: or, An Universal Dictionary of Arts and Sciences (1 изд.). London: James & John Knapton; John Darby; and others. Two volumes in folio.
- ^ Alston, R. C. (1974). A Bibliography of the English Language from the Invention of Printing to the Year 1800
 . Ilkley: Janus Press. See volume iii, items 535 through 544.
. Ilkley: Janus Press. See volume iii, items 535 through 544.
- ^ G. Garbrecht (ed., 1987). Hydraulics and Hydraulic Research: A Historical Review (A.A. Balkema). ISBN 90-6191-621-6
- ^ M. J. Lighthill (1995). Fluid mechanics, in Twentieth Century Physics ed. by L.M. Brown, A. Pais, and B. Pippard (IOP/AIP), Vol. 2, pp. 795–912.
- ^ „Hydrostatics”. Merriam-Webster. Приступљено 11. 9. 2018.
- ^ Anderson, John (1995). Computational Fluid Dynamics. McGraw-Hill Education. ISBN 978-0-07-001685-9.
- ^ Babinsky, Holger (новембар 2003), „How do wings work?” (PDF), Physics Education, 38 (6): 497—503, Bibcode:2003PhyEd..38..497B, S2CID 1657792, doi:10.1088/0031-9120/38/6/001
- ^ Chorin, Alexandre J.; Marsden, Jerrold E. (2013). A Mathematical Introduction to Fluid Mechanics. Springer. ISBN 978-1-4612-0883-9.
- ^ „Pascal's principle - Definition, Example, & Facts”. britannica.com. Архивирано из оригинала 2. 6. 2015. г. Приступљено 9. 5. 2018.
- ^ „Pascal's Principle and Hydraulics”. www.grc.nasa.gov. Архивирано из оригинала 05. 04. 2018. г. Приступљено 9. 5. 2018.
- ^ „Pressure”. hyperphysics.phy-astr.gsu.edu. Архивирано из оригинала 28. 10. 2017. г. Приступљено 9. 5. 2018.
Литература[уреди | уреди извор]
- Виктор Саљников Статика и кинематика флуида. Машински факултет у Београду. 1998. ISBN 978-86-395-0183-9..
- Скрипте са предавања из Механике флуида на Машинском факултету у Београду, 2000/2001
- Мирослав Бенишек, Светислав Чантрак, Милош Павловић, Цветко Црнојевић, Предраг Марјановић Механика флуида - Теорија и пракса. Машински факултет у Београду. 2005. ISBN 978-86-7083-531-3..
- Batchelor, George K. (1967). An Introduction to Fluid Dynamics. Cambridge University Press. ISBN 978-0-521-66396-0.
- Gregory, Falkovich (2011). Fluid Mechanics (A short course for physicists). Cambridge University Press. ISBN 978-1-107-00575-4.
- Kundu Pijush K; Cohen Ira M. (2008). Fluid Mechanics (4th revised изд.). Academic Press. ISBN 978-0-123-73735-9.
- G., Currie I. (1974). Fundamental Mechanics of Fluids. McGraw-Hill, Inc. ISBN 978-0-07-015000-3.
- Massey B., Ward-Smith J. (2005). Mechanics of Fluids (8th изд.). Taylor & Francis. ISBN 978-0-415-36206-1.
- White Frank M. (2003). Fluid Mechanics. McGraw-Hill. ISBN 978-0-07-240217-9.
- J. D. Anderson, Jr. (1997). A History of Aerodynamics (Cambridge University Press). ISBN 0-521-45435-2
- J. D. Anderson, Jr. (1998). Some Reflections on the History of Fluid Dynamics, in The Handbook of Fluid Dynamics (ed. by R.W. Johnson, CRC Press) Ch. 2.
- J. S. Calero (2008). The Genesis of Fluid Mechanics, 1640–1780 (Springer). ISBN 978-1-4020-6414-2
- O. Darrigol (2005). Worlds of Flow: A History of Hydrodynamics from the Bernoullis to Prandtl (Oxford University Press). ISBN 0-19-856843-6
- P. A. Davidson, Y. Kaneda, K. Moffatt, and K. R. Sreenivasan (eds, 2011). A Voyage Through Turbulence (Cambridge University Press). ISBN 978-0-521-19868-4
- M. Eckert (2006). The Dawn of Fluid Dynamics: A Discipline Between Science and Technology (Wiley-VCH). ISBN 978-3-527-40513-8
- H. Rouse and S. Ince (1957). History of Hydraulics (Iowa Institute of Hydraulic Research, State University of Iowa).
- G. A. Tokaty (1994). A History and Philosophy of Fluid Mechanics (Dover). ISBN 0-486-68103-3
- Nazarenko, Sergey (2014), Fluid Dynamics via Examples and Solutions, CRC Press (Taylor & Francis group), ISBN 978-1-43-988882-7
- Acheson, D. J. (1990). Elementary Fluid Dynamics. Clarendon Press. ISBN 0-19-859679-0.
- Chanson, H. (2009). Applied Hydrodynamics: An Introduction to Ideal and Real Fluid Flows. CRC Press, Taylor & Francis Group, Leiden, The Netherlands, 478 pages. ISBN 978-0-415-49271-3.
- Clancy, L. J. (1975). Aerodynamics. London: Pitman Publishing Limited. ISBN 0-273-01120-0.
- Lamb, Horace (1994). Hydrodynamics (6th изд.). Cambridge University Press. ISBN 0-521-45868-4. Originally published in 1879, the 6th extended edition appeared first in 1932.
- Milne-Thompson, L. M. (1968). Theoretical Hydrodynamics (5th изд.). Macmillan. Originally published in 1938.
- Shinbrot, M. (1973). Lectures on Fluid Mechanics. Gordon and Breach. ISBN 0-677-01710-3.
- Encyclopedia: Fluid dynamics Scholarpedia
- Mario Bunge, Philosophy of Science: From Explanation to Justification, . Bunge, Mario (1998). Philosophy of Science: From Explanation to Justification. Transaction Publishers. ISBN 1412830834.
- Spellman, Frank R.; Whiting, Nancy E. (2005). Environmental engineer's mathematics handbook. CRC Press. ISBN 978-1-56670-681-0.
- Fontana, Fabrizio; DiCapua Roberto (2005). „Role of hydrostatic paradoxes towards the formation of the scientific thought of students at academic level”. European Journal of Physics. 26 (6): 1017—1030. Bibcode:2005EJPh...26.1017F. S2CID 120595888. doi:10.1088/0143-0807/26/6/009.
- Christodoulou, Demetrios (октобар 2007). „The Euler Equations of Compressible Fluid Flow” (PDF). Bulletin of the American Mathematical Society. 44 (4): 581—602. doi:10.1090/S0273-0979-07-01181-0
 .
. - Euler, Leonhard (1757). „Principes généraux du mouvement des fluides” [The General Principles of the Movement of Fluids]. Mémoires de l'académie des sciences de Berlin (на језику: француски). 11: 274—315.
- Fay, James A. (1994). Introduction to Fluid Mechanics. MIT Press. ISBN 978-0-262-06165-0.
- Friedlander, S.; Serre, D., ур. (2003). Handbook of Mathematical Fluid Dynamics – Volume 2. Elsevier. ISBN 978-0-444-51287-1.
- Friedmann, A. (1934) [1922]. Kochin, Nikolai, ур. Опыт гидромеханики сжимаемой жидкости [An essay on hydrodynamics of compressible fluid] (на језику: руски). Petrograd.
- Gibbon, J.D.; Moore, D.R.; Stuart, J.T. (2003). „Exact, infinite energy, blow-up solutions of the three-dimensional Euler equations”. Nonlinearity. 16 (5): 1823—1831. Bibcode:2003Nonli..16.1823G. S2CID 250797052. doi:10.1088/0951-7715/16/5/315.
- Henderson, L.F. (2000). „General Laws for the Propagation of Shock-waves through Matter”. Ур.: Ben-Dor, Gabi; Igra, Ozer; Elperin, Tov. Handbook of Shock Waves, Three Volume Set. Elsevier. ISBN 978-0-08-053372-8.
- Hunter, John K. (25. 9. 2006), An Introduction to the Incompressible Euler Equations (PDF), Приступљено 2019-05-31
- 今井 功 (IMAI, Isao) (новембар 1973). 『流体力学(前編)』 [Fluid Dynamics 1] (на језику: Japanese). 裳華房 (Shoukabou). ISBN 4-7853-2314-0.
- Landau, L D; Lifshitz, E. M. (2013). Fluid Mechanics. Elsevier. ISBN 978-1-4831-4050-6.
- Marchioro, C.; Pulvirenti, M. (1994). Mathematical Theory of Incompressible Nonviscous Fluids. Applied Mathematical Sciences. 96. New York: Springer. ISBN 0-387-94044-8.
- Quartapelle, Luigi; Auteri, Franco (2013). Fluidodinamica comprimibile [Compressible Fluid Dynamics] (на језику: италијански). CEA. ISBN 978-88-08-18558-7.
- Toro, E. F. (1999). Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction. Springer. ISBN 978-3-540-65966-2.
- Valorani, Mauro; Nasuti, Francesco (n.d), Metodi di analisi delle turbomacchine (PDF), Sapienza - Universit`a di Roma, Архивирано из оригинала (PDF) 16. 05. 2022. г., Приступљено 2019-05-31
- Zingale, M. (16. 4. 2013), Notes on the Euler equations (PDF), Архивирано из оригинала (PDF) 19. 06. 2015. г., Приступљено 2019-05-31
- Badin, G.; Crisciani, F. (2018). Variational Formulation of Fluid and Geophysical Fluid Dynamics - Mechanics, Symmetries and Conservation Laws -. Springer. стр. 218. Bibcode:2018vffg.book.....B. ISBN 978-3-319-59694-5. S2CID 125902566. doi:10.1007/978-3-319-59695-2.
- Batchelor, G. K. (1967). An Introduction to Fluid Dynamics. Cambridge University Press. ISBN 0-521-66396-2.
- Thompson, Philip A. (1972). Compressible Fluid Flow. New York: McGraw-Hill. ISBN 0-07-064405-5.
Спољашње везе[уреди | уреди извор]
- Calvert, J. B. (2003). „Hydrostatics”. University of Denver. Приступљено 22. 5. 2013.
- Hydrostatics Pressure Calculator.
- Ayman, Mohammad (2003). „Hydrostatics”. University of Denver. Приступљено 2013-05-22.











