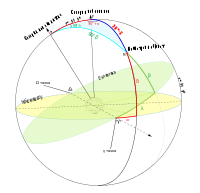
Небески координатни системи

2 — центар Млечног пута
3 — галактички екватор
4 — северни галактички пол
6 — еклиптика
7 — северни пол еклиптике
9 — небески екватор
10 — северни небески пол
11 — γ тачка (тачка пролећне равнодневице)
12 — Ω тачка (тачка јесење равнодневице)
Сунце (5) и Земља (8) су приказани да би се уочило њихово кретање, и нису дати у размери.
Небески координатни системи су координатни системи који се користе за описивање положаја астрономских објеката у (на) небеској сфери. Развијен је већи број небеских координатних система, а користи се увек онај најпогоднији за описивање датог објекта или појаве.[1] Ови координатни системи се по правилу заснивају на сферном координатном систему, а међусобно се разликују по координатном почетку и смеровима у којима су правци оса. Према положају координатног почетка се могу поделити на:[2][тражи се бољи извор]
- топоцентричне — са центром у посматрачу,
- планетоцентричне — са центром у некој од планета (мора да буде одређена при дефинисању координатног система),
- геоцентричне — са центром у центру Земље,
- селеноцентричне — са центром у центру Месеца,
- хелиоцентричне — са центром у центру Сунца,
- барицентричне — са центром у центру масе Сунчевог система.
Сферни координатни систем[уреди | уреди извор]
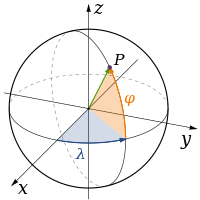
Сферни координатни систем је дефинисан координатним почетком и правцима ка којима су усмерене осе. Раван xy се назива основна раван. Сферне координате су удаљеност од координатног почетка (r или ρ), угао између позитивног смера x-осе и пројекције посматране тачке на основну раван (лонгитуда, на слици обележена са λ, у литератури се срећу и θ и φ), као и угао између посматране тачке и основне равни (латитуда, на слици φ, може бити обележен и са β или θ). У математици се уместо угла између тачке и основне равни често користи њему комплементаран угао — угао између тачке и z-осе (колатитуда). Ако је удаљеност од координатног почетка фиксна (код небеских координатних система се сматра да је бесконачна, в. небеска сфера), за опис положаја су довољне две угловне координате.[2][3]
Хоризонтски координатни систем[уреди | уреди извор]

Из перспективе посматрача, најприроднији координатни систем је хоризонтски координатни систем. Координатни почетак је у посматрачу, а основна раван је хоризонт, односно раван тангентна на Земљу у тачки у којој се налази посматрач. Тачка директно изнад посматрача се назива зенит, док је њена антиподна тачка надир. Координате су хоризонтска висина и азимут. Хоризонтска висина (a) је угао између посматраног објекта и равни хоризонта. Некада се уместо хоризонтске висине користи зенитна даљина (z), која је комплементарна хоризонтској висини[4]:
Азимут (A) је угао између одабраног смера и пројекције посматраног објекта на раван хоризонта. Азимут може да се мери од смера севера или југа, и то или у смеру казаљке на сату (ретроградан, математички негативан смер) од 0° до 360°, или на оба смера од 0° до 180°, због чега је при интерпретацији хоризонтских координата потребно обратити пажњу како је аутор дефинисао азимут.[1][2][4] У овом чланку, азимут се мери од севера у смеру казаљке на сату (север: A = 0° ; исток: A = 90°; југ: A = 180° ; запад: A = 270°).
Велики круг на небеској сфери који садржи северни и јужни небески пол се назива меридијан и нормалан је на небески екватор, а може се схватити и као пројекција земаљског меридијана на небеску сферу. Меридијан који пролази и кроз зенит и надир је локални меридијан датог посматрача, и садржи и северну и јужну тачку хоризонта тог посматрача. Сунце и звезде имају највишу хоризонтску висину (кулминирају) када пролазе кроз локални меридијан.[1][2]
Екваторијални координатни систем[уреди | уреди извор]
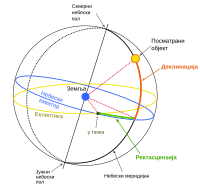
Друга природна основна раван за посматраче на Земљи је раван екватора. Како приликом ротације и револуције Земље смер Земљине осе остаје практично непромењен, то се не мења ни положај равни нормалне на ову осу, а то је раван екватора. Угао који објекти заклапају са овом равни се назива деклинација. Деклинација се обележава словом δ и изражава у степенима; тачке северно од екватора имају позитивну а јужно од екватора негативну деклинацију. Тако деклинација северног небеског пола износи +90°, а јужног небеског пола -90°.[1][2][4]
С обзиром на чињеницу да је небески екватор нагнут у односу на раван Земљине орбите еклиптике, постоје само две пресечне тачке ових равни (посматрано као два велика круга на небеској сфери) — тачка пролећне (γ тачка) и тачка јесење равнодневице (Ω тачка). Положај γ тачке на небеској сфери је релативно фиксан (услед прецесије, γ тачка направи један пун круг по еклиптици за око 25800 година), тако да је она погодна полазна тачка за мерење угла на екватору и на еклиптици. Угао између γ тачке и пројекције објекта на раван небеског екватора мерен у директном смеру (математички позитиван смер, смер супротан кретању казаљке на сату) се назива ректасцензија и обележава се словом α. Референтни систем чије су координате ректасцензија и деклинација се назива небески екваторијални координатни систем, и најчешће је коришћени небески координатни систем за одређивање положаја тела ван Сунчевог система (каталози звезда и објеката дубоког неба), јер се координате ових тела врло мало мењају у небеском екваторијалном координатном систему (само услед прецесије и сопственог кретања, а диурнално и годишње кретање Земље нема утицаја). Ректасцензија се може изражавати у угловним степенима, минутима и секундама, или у сатима, временским минутима и временским секундама (1 час одговара углу од 15°, с обзиром на то да Земља направи пун круг (360°) за 24 часа).[1][2][4]

Уместо смера γ тачке, као референтан смер се може одабрати локални југ, односно локални меридијан. Угао мерен од југа ка посматраном објекту у смеру казаљке на сату се назива часовни угао (h), и показује колико је времена прошло откако се објект налазио у локалном меридијану. Деклинација и часовни угао су координате месног екваторијалног координатног система. Часовни угао γ тачке је локално сидеричко време (θ). Важи однос[4]
Сидеричко време и часовни угао се чешће изражавају у сатима, временским минутима и временским секундама него у угловним мерама.[2] Сви објекти који имају исту ректасцензију имају и исти часовни угао, због чега се полукружница дефинисана фиксном ректасцензијом назива и часовна кружница. Узимајући ову дефиницију у обзир, може се рећи да је часовни угао угао између локалног меридијана и часовне кружнице.[1]
Епоха[уреди | уреди извор]
Положај звезда и других небеских тела ван Сунчевог система се по правилу даје у односу на небески екваторијални координатни систем. Међутим, с обзиром на пертурбације које трпи Земља на својој орбити (прецесија, нутација, пертурбација путање под утицајем других планета), елементи координатног система морају бити једнозначно дефинисани. У ту сврху се дефинише одговарајућа „епоха“, како би се знало на који тренутак се односе координате (екваторијалне и еклиптичке). Тренутно је у употреби епоха J2000.0 (1. јануар 2000. године у подне, по универзалном времену), заснована на Фундаменталном каталогу 5 који је објављен 1988. године и садржи референтне податке за 3117 фундаменталних звезда.[1]
Еклиптички координатни систем[уреди | уреди извор]
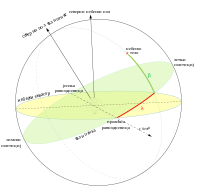

Еклиптика — раван Земљине орбите или велики круг на небеској сфери дефинисан годишњим кретањем Сунца — основна је раван још једног важног координатног система, по њој названог еклиптички координатни систем. Постоје три верзије у зависности од положаја координатног почетка: топоцентрична, геоцентрична и хелиоцентрична. За удаљене објекте, разлика међу њима је занемарљива, али не и у случају тела Сунчевог система.[4]
Поред угла између објекта и еклиптике (еклиптичка латитуда, β), други угао је еклиптичка лонгитуда (λ) — угао између пројекције објекта на раван еклиптике и γ тачке, која је погодна јер је деле еклиптика и небески екватор. Еклиптичка латитуда је позитивна северно од еклиптике, а негативна јужно од еклиптике. Северни и јужни еклиптички пол имају латитуду +90° и -90°, респективно. Северни и јужни небески пол, услед прецесије, круже око северног и јужног пола еклиптике.[1][4]
Хелиоцентрична еклиптичка латитутда и лонгитуда се обележавају са β’ и λ’, а за превођење из геоцентричних у хелиоцентричне еклиптичке координате је потребно знати и удаљеност до посматраног објекта. Конверзија се онда најлакше ради превођењем координата објекта у Декартове координате, прерачунавањем координата у односу на нови координатни почетак (све осе остају паралелне) и затим прерачунавањем координата из правоуглих у нове сферне.[4]
Еклиптички координатни систем је нарочито погодан за представљање положаја тела Сунчевог система, јер планете (и њихови сателити) мало одступају од равни еклиптике, тако да увек имају малу латитуду. Геоцентрична еклиптичка латитуда Сунца и хелиоцентрична еклиптичка латитуда Земље су практично нула.[4]
Галактички координатни систем[уреди | уреди извор]

Галактички координатни систем је хелиоцентрични небески координатни систем чија је основна раван раван Млечног пута. С обзиром да Сунце лежи врло близу галактичкој равни, било је могуће сместити центар овог координатног система у центар Сунца. Координате су галактичка латитуда (b, позитивна на север, негативна на југ) и галактичка лонгитуда (l). Галактичка лонгитуда се мери у директном смеру од средишта Млечног пута, за које се сматра црна рупа, која представља снажан извор радио зрачења и означава се Sagittarius A*. Sagittarius A* има, дакле, галактичке координате l = 0°, b = 0°, док су његове екваторијалне координате α = 17h 45,7min, δ = -29° 00’. Еклиптичке координате галактичког северног пола су α = 12h 51,4min, δ = +27° 08’.[4]
Овакав референтни систем је Међународна астрономска унија дефинисала тек 1959. године, након што је утврђен положај средишта Галаксије. Пре тога је галактичка лонгитуда рачуната од пресека небеског екватора са равни Галаксије. Данас се за галактичке координате по старом систему користе ознаке l I и b I.[4]
Супергалактички координатни систем[уреди | уреди извор]
Релативну планарну дистрибуцију маглина уочио је још Вилхелм Хершел, а Жерар де Вокулор је средином 20. века потврдио проучавањем каталога, постојање супергалактичке равни, у чијој близини лежи већина група галаксија и галактичких кластера које припадају локалном суперкластеру суперкластеру Девица. Супергалактички северни пол има галактичке координате l = 47,37°, b = + 6,32°, а основни правац је дефинисан пресеком са равни галаксије и има координате 'l = 137,37°, b = 0°. [5]
Трансформације координата[уреди | уреди извор]
С обзиром на то да каталози објеката ван Сунчевог система (звезде, маглине, галаксије...) најчешће користе екваторијалне координате, по правилу се трансформације небеских координата врше преко екваторијалних координата. У даљем тексту се користе следеће ознаке:
- A — азимут (рачунат од севера)
- a — хоризонтска висина
- z — зенитна даљина (90° - a)
- φ — географска ширина посматрача
- δ — деклинација
- α — ректасцензија
- h — часовни угао
- ε — нагиб еклиптике (угао између еклиптике и небеског екватора)
- λ — еклиптичка лонгитуда
- β — еклиптичка латитуда
- l — галактичка лонгитуда
- b — галактичка латитуда

За извођење трансформација координата једног небеског координатног система у други, потребно је познавати 2 теореме сферне тригонометрије — синусну и косинусну теорему.[4]
- Синусна теорема за сферни троугао гласи да је у датом сферном троуглу, однос синуса углова и синуса њима наспрамних страница константан:
- Косинусна теорема сферне тригонометрије је:
Хоризонтске и екваторијалне координате[уреди | уреди извор]

Ако су дате координате у хоризонтском систему (висина а и азимут А), и ако је позната географска ширина посматрача (φ), тада су одговарајуће екваторске координате:[4]
Ако су познате екваторске координате (часовни угао t и деклинација δ), као и географска ширина посматрача, тада су одговарајуће хоризонтске координате:[4]
Прве две једначине из оба сета не смеју да се деле, јер би се добио тангнес часовног угла (односно азимута), а тангенс углова не разликује углове у првом и трећем квадранту, односно у другом и четвртом квадранту.
Веза између ректасцензије (α) и часовног угла је
где је θ локално сидеричко време.
Екваторијалне и еклиптичке координате[уреди | уреди извор]
Ако су дате деклинација и ректасцензија неког објекта, тада се његове геоцентричне еклиптичке координате могу израчунати на следећи начин:[4]
Обрнуто, екваторијалне координате се из геоцентричних еклиптичких могу израчунати помоћу следећих једначина:[4]
Екваторијалне и галактичке координате[уреди | уреди извор]
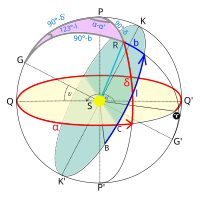
Нека је lN галактичка лонгитуда северног небеског пола (123,0°), а αP и δP ректасцензија и деклинација северног галактичког пола (αP = 12h 51,4min, δP = 27° 08’). Тада важе следеће релације:[4]
Види још[уреди | уреди извор]
- Сферни координатни систем
- Сферна тригонометрија
- Географске координате
- Прецесија
- Нутација
- Нагиб еклиптике
- Звездано време
Референце[уреди | уреди извор]
- ^ а б в г д ђ е ж Patrick Moore, ур. (2002). Philip's Astronomy Encyclopedia. Philip's. ISBN 978-0-540-07863-9.
- ^ а б в г д ђ е Murdin, Paul, ур. (2001). Encyclopedia of Astronomy and Astrophysics (на језику: (језик: енглески)). Institure of Physics Publishing. ISBN 978-0-7503-0440-5.
- ^ Tanton, James (2005). Encyclopedia of Mathematics. New York: Facts on File, Inc. ISBN 978-0-8160-5124-3.
- ^ а б в г д ђ е ж з и ј к л љ м н њ Hannu Karttunen, Pekka Kröger, Heikki Oja, Markku Poutanen, Karl Johan Donner, ур. (2007). Fundamental Astronomy (на језику: енглески) (5th изд.). Berlin: Springer. стр. 21. ISBN 978-3-540-34143-7.
- ^ P., Lahav, O. Santiago, B. X. Webster, A. M. Strauss, M. A. Davis, M. Dressler, A. Huchra, J. (1998-09-27). The Supergalactic Plane revisited with the Optical Redshift Survey. стр. 166—176. OCLC 691241738.
Литература[уреди | уреди извор]
- Patrick Moore, ур. (2002). Philip's Astronomy Encyclopedia. Philip's. ISBN 978-0-540-07863-9.
- Murdin, Paul, ур. (2001). Encyclopedia of Astronomy and Astrophysics (на језику: (језик: енглески)). Institure of Physics Publishing. ISBN 978-0-7503-0440-5.
- Tanton, James (2005). Encyclopedia of Mathematics. New York: Facts on File, Inc. ISBN 978-0-8160-5124-3.
- Hannu Karttunen, Pekka Kröger, Heikki Oja, Markku Poutanen, Karl Johan Donner, ур. (2007). Fundamental Astronomy (на језику: енглески) (5th изд.). Berlin: Springer. стр. 21. ISBN 978-3-540-34143-7.
Спољашње везе[уреди | уреди извор]
- Positional Astronomy — Сферна тригонометрија, небески координатни системи, трансформације координата, и пратећи задаци (језик: енглески)
- Конверзија галактичких у друге небеске координате (језик: енглески)
- Стандарди фунфаменталне астрономије (Међународна астрономска унија) — сет алгоритама и процедура који имплементирају стандардне моделе који се користе у фундаменталној астрономији (доступан за Фортран и C) (језик: енглески)
- Naval Observatory Vector Astrometry Software (NOVAS) Архивирано на сајту Wayback Machine (28. јун 2015) — интегрисани пакет процедура за различите прорачуне у позиционој астрономији (доступан за Фортран, C и Пајтон) (језик: енглески)






















