Узгон


Узгон је компонента укупне аеродинамичке силе, нормална на правац кретања тела кроз ваздух. Обележава се са Rz и делује при кретању тела кроз ваздух, уравнотежујући његову тежину, слично као при потапању у течност. Узгон се повезује са крилом авиона, краковима елисе, лопатицама турбине, хидрокрилима глисера, спојлерима аутомобила итд. Све те површине имају заједничко, да им је попречни пресек (у правцу кретања) облика аеропрофила. Узгон је резултат створене разлике притиска, са горње и доње стране аеропрофила.[1]
Општа дефиниција[уреди | уреди извор]
Аеростатички потисак је једнак тежини ваздуха запремине тела, које мирује у њему. За разлику од хидростатичког потиска, аеростатички је занемарљиво мале величине. Сила потиска, односно узгон, може се постићи са асиметричним опструјавањем ваздуха око тела. Асиметрично опструјавање се постиже ако се тело профилише, у пресеку са равни у којој се жели постићи вектор узгона, добијена контура је аеропрофил. Ако се такво тело закрене под већи поставни (нападни) угао α у односу на правац кретања, узгон се још више повећава. Може се то постићи и са равном плочом постављеном под нападни угао, у односу на правац кретања.[1]
У аеродинамици се користе бездимензионе аналитичке релације, те се и аеродинамичке силе и моменти своде на бездимензионе коефицијенте.
|
Где су:
|
Сагласно томе је дефинисан и узгон:
Где су:
|
| У аеродинамичким прорачунима се често користи градијент коефицијента узгона по нападном углу α (види дијаграм доле), то је у ствари један од дериватива стабилности: |
 |
 |
силе и момента аеропрофила |
функцији нападног угла |
Узгон аеропрофила[уреди | уреди извор]
Постоји више начина за објашњење физикалности генерисања узгона помоћу аеропрофила. У међувремену су се неки показали као и нетачни.[1]
|
Њутнов закон[уреди | уреди извор]
Један од прилаза за објашњење принципа појаве узгона јесте помоћу Њутновог закона, по коме је узгон последица убрзавања ваздушне струје према доњој страни узгонске површине. За тај прилаз, добар је пример ротор хеликоптера, који са својим крацима убрзава ваздух надоле, а реакција на то је сила узгона. Тај принцип се може квантитативно изразити као последица промене импулса у струјном пољу ваздуха:
Са закривљеношћу аеропрофила и са повећањем нападног угла α, подешава се убрзавање ваздушне струје надоле, па и интензитет узгона.[1]
Популарни принцип, „дужи пут за исто време“[уреди | уреди извор]
Једноставан и врло раширен принцип објашњавања генерисања узгона на аеропрофилу, познат је по називу „пређени различит пут за исто време“. Заснива се на поставци да честице, које се крећу по дужој кривини, имају већу брзину, да би сустигле остале у завршној тачки. На основу тога што је при већој брзини мањи статички притисак и обрнуто, ствара се разлика притиска на горњаци и доњаци аеропрофила (илустрација на доњим сликама). Резултат дејства разлике притиска на одређену површину ствара силу узгона аеропрофила, односно крила авиона у целини. Тај принцип се заснива на једначини Бернулија. Тај принцип побија амерички аеродинамичар професор Џон Андерсон (en:John D. Anderson). Тврди да то једноставно није тачно, без обзира што је ово објашњење за принцип генерисања узгона најчешће примењивано. То поткрепљује са стручним радовима, а и са симулацијом, приказаном на слици доле, на којој је приказано кашњење честица ваздуха које прелазе дужи пут.[а] Дискредитовањем примене Бернулијеве једначине у овоме принципу, није довођен у питање сам Бернулијев принцип.[4][5][6][7][8][9]
Комплекснији приступ[уреди | уреди извор]

Генерисање узгона је у складу са основним, релевантним принципима физике:
- Њутнови закони,
- Једначина континуитета (очување масе), укључујући и чињеницу да аеропрофил приморава ваздух да га опструјава и
- утицај притиска и трења на карактеристике струјања.
Према последњем принципу, притисак зависи од осталих параметара струјања, као што је густина, термодинамичко стање и вискозност. Тангенцијални напон вискозног гаса одређује се са Навје-Стоксовим једначинама. У многим случајевима, задовољава и апроксимација са укидањем описа међусобног утицаја слојева ваздушне струје, у већем делу струјног тока, то јест са занемаривањем вискозности. Такво струјање се дефинише са Ојлеровим једначинама, уместо са Навје-Стоксовим. При мањим Маховим бројевима стишљивост се занемарује. Са овим прилазима поправљају се резултати, добијени само на основу Бернулијеве једначине. Произилази да, од многих коришћених метода објашњавања генерисања узгона, већина појединачно коришћених нису довољне, односно тачне, као нпр. изоловано коришћен Бернули или Њутнов закон о кретању. Ниво апроксимација и избор метода дефиниције је приказан са блок шемом на доњој слици. Увођење утицаја стишљивости и сличности струјања постиже се са корекцијама помоћу Маховог и Рејнолдсовог броја.
Теорема Жуковског[уреди | уреди извор]

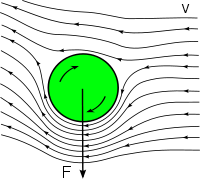
Теорема Жуковског је основна теорема аеродинамике, развијена је почетком 20. века. Односи се на генерисање узгона на цилиндру, при његовом опструјавању са флуидом са циркулацијом. Ти резултати се односе и на аеропрофил, физикалност је потпуно иста, у питању је дводимензионално струјање. Теорема Жуковског се односи на аналитичко одређивање аеродинамичке силе узгона, при струјању флуида око цилиндра.
За уопштавање и поједностављење оваквог струјања уведен је појам циркулације брзине, поједностављено речено циркулације. У питању је математичка дефиниција елементарне циркулације, а са интеграцијом се добија укупна: [13][14]
Расподела брзине је основа за одређивање расподеле притиска. На елеменат површине цилиндра (обележено црвено на слици десно) ds = dx dy, делује елементарна сила услед притиска, а ту силу сачињавају компоненте:
На основу Бернулијеве једначине одређује се притисак:
| После замене, математичких трансформација и извршене интеграције добија се резултат: |
|
Овај резултат представља силу узгона по теореми Жуковског, која делује по јединици дужине цилиндра. Са множењем, добијеног резултата, са укупном дужином цилиндра L, добија се укупни узгон. При овоме се подразумева да је дуж целе дужине цилиндра раванско струјање.
|
|
За лакше разумевање овога феномена, погодно је посматрати Магнусов ефекат, код кога се генерише узгон са принудном ротацијом цилиндра, у слободној струји ваздуха. У овом случају се циркулација изазива са принудном ротацијом преко граничног слоја и на једној страни се ваздух убрзава а на супротној успорава. Асиметрија поља брзина значи и асиметрија притиска, а та разлика значи стварање силе узгона. Овај ефекат се доста користи у спортовима са лоптом, посебно у тенису и фудбалу. На начин, остварује се криволинијска путања лопте.[15]
Интеграција расподеле притиска[уреди | уреди извор]
Узгон се може одредити на основу разлике притиска изнад и испод крила, што се повезује са расподелом брзине изнад и испод крила, преко Бернулијеве једначине. Да би се одредила разлика притиска изнад и испод крила мора се расподела локалних вредности интегралити. На тај начин се одреди укупна сила узгона, за цело крило са једначином:
Где су:
|
У горњој једначини је занемарен утицај трења граничног слоја и коре узгонске површине. Тај утицај на узгон је иначе занемарљив, те ова околност не деградира резултате.
Претходна формула дефинише узгон аеропрофила, то јест за дводимензијално (2D) струјање. За узгон крила, коначног размаха, потребно је извршити поправке утицаја крајева, то јест за услове 3D струјања.
Експериментално одређивање[уреди | уреди извор]
Са мерењем се узгон одређује у лету и у аеротунелима. У лету се мере перформансе, па на основу познавања других релевантних података, посредно се израчунава узгон летелице.
У аеротунелима се мери расподела притиска и на описани начин се са принципом интеграције одреди узгон. Такође се у аеротунелима, узгон директно мери, са аеровагама.
Напомене[уреди | уреди извор]
Види још[уреди | уреди извор]
Референце[уреди | уреди извор]
- ^ а б в г „Физикалност летења”. Архивирано из оригинала 19. 07. 2011. г. Приступљено 22. 04. 2010.
- ^ "The wing deflects the airflow such that the mean velocity vector behind the wing is canted slightly downward (…). Hence, the wing imparts a downward component of momentum to the air; that is, the wing exerts a force on the air, pushing the flow downward. From Newton's third law, the equal and opposite reaction produces a lift."
- ^ Rendulić 1960, стр. 103–130
- ^ „Узгон због скретања струјања”. Архивирано из оригинала 05. 07. 2011. г. Приступљено 22. 04. 2010.
- ^ Anderson 2004, стр. 355.
- ^ „Визуализација струјања”. Приступљено 22. 04. 2010.
- ^ {{Cite web|url=http://www.av8n.com/fly/lift.htm |title=Полемика о томе „како авион лети“, Приступљено 22. 4. 2010.
- ^ „Принципи лета”. Приступљено 22. 04. 2010.
- ^ „Бернули” (PDF). Архивирано из оригинала (PDF) 28. 11. 2009. г. Приступљено 22. 04. 2010.
- ^ а б Aerodinamika, Masinski fakultet Beograd, 1992.g.,glava 1, pp. 13–17,Prof. dr Tomislav Dragović dipl. ing.
- ^ „Бернули и Њутн”. Архивирано из оригинала 07. 02. 2006. г. Приступљено 22. 04. 2010.
- ^ „Бернули или Њутн”. Архивирано из оригинала 21. 01. 2010. г. Приступљено 22. 04. 2010.
- ^ Rendulić 1960, стр. 42.
- ^ Инг Златко Рендулић (1960). Аеродинамика, Основи динамике флуида (на језику: (језик: српски)). Београд: Команда РВ и ПВО. стр. 42.
- ^ Rendulić 1960, стр. 82–85.
Литература[уреди | уреди извор]
- Инг Златко Рендулић (1960). Аеродинамика, Основи динамике флуида (на језику: (језик: српски)). Београд: Команда РВ и ПВО. стр. 42.
- Anderson, John D. Jr. (2004). Introduction to Flight (5th изд.). McGraw-Hill. стр. 355.
- Osnovi aerodinamičkih konstrukcija, prvi deo, Naučna knjiga, Beograd, 1950.g., Prof. univerziteta Miroslav Dr Nenadović dipl. ing.
- Rendulić, Zlatko (1960). Aerodinamika. Beograd.
- Abbott, I. H.; von Doenhoff, A. E. (1958), Theory of Wing Sections, Dover Publications
- Anderson, D. F.; Eberhardt, S. (2001), Understanding Flight, McGraw-Hill
- Anderson, J. D. (1991), Fundamentals of Aerodynamics, 2nd ed., McGraw-Hill
- Anderson, J. D. (1995). Computational Fluid Dynamics, The Basics With Applications. McGraw-Hill. ISBN 978-0-07-113210-7.
- Anderson, J. D. (1997), A History of Aerodynamics, Cambridge University Press
- Anderson, J. D. (2008), Introduction to Flight, 6th edition, McGraw Hill
- Aris, R. (1989), Vectors, Tensors, and the basic Equations of Fluid Mechanics, Dover Publications
- Auerbach, D. (2000), „Why Aircraft Fly”, Eur. J. Phys., 21 (4): 289—296, Bibcode:2000EJPh...21..289A, S2CID 250821727, doi:10.1088/0143-0807/21/4/302
- Babinsky, H. (2003), „How do wings work?”, Phys. Educ., 38 (6): 497—503, Bibcode:2003PhyEd..38..497B, S2CID 1657792, doi:10.1088/0031-9120/38/6/001
- Batchelor, G. K. (1967), An Introduction to Fluid Dynamics, Cambridge University Press
- Clancy, L. J. (1975), Aerodynamics, Longman Scientific and Technical
- Craig, G. M. (1997), Stop Abusing Bernoulli, Anderson, Indiana: Regenerative Press
- Durand, W. F. (1932), Aerodynamic Theory, vol. 1, Dover Publications
- Eastlake, C. N. (2002), „An Aerodynamicist's View of Lift, Bernoulli, and Newton”, The Physics Teacher, 40 (3): 166—173, Bibcode:2002PhTea..40..166E, doi:10.1119/1.1466553
- Jeans, J. (1967), An Introduction to the Kinetic theory of Gasses, Cambridge University Press
- Kulfan, B. M. (2010), Paleoaerodynamic Explorations Part I: Evolution of Biological and Technical Flight, AIAA 2010-154
- Lanchester, F. W. (1907), Aerodynamics, A. Constable and Co.
- Langewiesche, W. (1944), Stick and Rudder - An Explanation of the Art of Flying, McGraw-Hill
- Lissaman, P. B. S. (1996), The facts of lift, AIAA 1996-161
- Marchai, C. A. (1985), Sailing Theory and Practice, Putnam
- McBeath, S. (2006), Competition Car Aerodynamics, Sparkford, Haynes
- McLean, D. (2012), Understanding Aerodynamics - Arguing from the Real Physics, Wiley
- Milne-Thomson, L. M. (1966), Theoretical Aerodynamics, 4th ed., Dover Publications
- Prandtl, L.; Tietjens, O. G. (1934), Applied Hydro- and Aeromechanics, Dover Publications
- Raskin, J. (1994), 09. 2007 Coanda Effect: Understanding Why Wings Work Проверите вредност параметра
|archiveurl=(помоћ), Архивирано из оригинала 2007-09-28. г. - Schlichting, H. (1979), Boundary-Layer Theory, Seventh Ed., McGraw-Hill
- Shapiro, A. H. (1953), The Dynamics and Thermodynamics of Compressible Fluid Flow, Ronald Press Co.
- Smith, N. F. (1972), „Bernoulli and Newton in Fluid Mechanics”, The Physics Teacher, 10 (8): 451—455, Bibcode:1972PhTea..10..451S, doi:10.1119/1.2352317
- Spalart, P. R. (2000), Strategies for turbulence modeling and simulations, 21 (3), International Journal of Heat and Fluid Flow, стр. 252
- Sumer, B.; Mutlu Fredsøe, Jørgen (2006), Hydrodynamics around cylindrical structures (revised ed.)
- Thwaites, B. (1958), Incompressible Aerodynamics, Dover Publications
- Tritton, D. J. (1980), Physical Fluid Dynamics, Van Nostrand Reinhold
- Van Dyke, M. (1969), „Higher-Order Boundary-Layer Theory”, Annual Review of Fluid Mechanics, 1 (1): 265—292, Bibcode:1969AnRFM...1..265D, doi:10.1146/annurev.fl.01.010169.001405
- von Mises, R. (1959), Theory of Flight, Dover Publications
- Waltham, C. (1998), „Flight without Bernoulli”, The Physics Teacher, 36 (8): 457—462, Bibcode:1998PhTea..36..457W, doi:10.1119/1.879927
- Weltner, K. (1987), „A comparison of explanations of the aerodynamic lifting force”, Am. J. Phys., 55 (1): 53, Bibcode:1987AmJPh..55...50W, doi:10.1119/1.14960
- White, F. M. (1991), Viscous Fluid Flow, 2nd ed., McGraw-Hill
- Wille, R.; Fernholz, H. (1965), „Report on the first European Mechanics Colloquium, on the Coanda effect”, J. Fluid Mech., 23 (4): 801—819, Bibcode:1965JFM....23..801W, S2CID 121981660, doi:10.1017/s0022112065001702
- Williamson, C. H. K.; Govardhan, R (2004), „Vortex-induced vibrations”, Annual Review of Fluid Mechanics, 36: 413—455, Bibcode:2004AnRFM..36..413W, S2CID 58937745, doi:10.1146/annurev.fluid.36.050802.122128
- Zdravkovich, M. M. (2003). Flow around circular cylinders 2. Oxford University Press. стр. 850—855. ISBN 978-0-19-856561-1.
- Introduction to Flight, John D. Anderson, Jr. Introduction to Flight. McGraw-Hill. 2005. ISBN 978-0-07-299071-3. – Dr. Anderson is Curator of Aerodynamics at the Smithsonian Institution's National Air & Space Museum and Professor Emeritus at the University of Maryland.
- David Anderson and Scott Eberhardt (2001). Understanding Flight. McGraw-Hill. ISBN 978-0-07-136377-8. – A physicist and an aeronautical engineer explain flight in non-technical terms and specifically address the equal-transit-time myth. They attribute airfoil circulation to the Coanda effect, which is controversial.
- Aerodynamics, Clancy, L. J. Section 4.8, Pitman Publishing Limited. Clancy, Laurence J. (1975). Aerodynamics. London. ISBN 978-0-273-01120-0..
- Aerodynamics, Aeronautics, and Flight Mechanics, McCormick, Barnes W., Chapter 3, John Wiley & Sons, Inc. McCormick, Barnes W. (1979). Aerodynamics, Aeronautics and Flight Mechanics. New York. ISBN 978-0-471-03032-4..
- Fundamentals of Flight, Richard S. Shevell, Prentice-Hall International Editions. ISBN 978-0-13-332917-9. – This is a text for a one-semester undergraduate course in mechanical or aeronautical engineering. Its sections on theory of flight are understandable with a passing knowledge of calculus and physics.
- Craig, Paul P.; Pellam, John R. (1957). „Observation of Perfect Potential Flow in Superfluid”. Physical Review. 108 (5): 1109—1112. Bibcode:1957PhRv..108.1109C. doi:10.1103/PhysRev.108.1109. – Experiments under superfluidity conditions, resulting in the vanishing of lift in inviscid flow since the Kutta condition is no longer satisfied.
- Crummer, Charles A. (2005). „Aerodynamics at the Particle Level”. Bibcode:2005nlin......7032C. arXiv:nlin/0507032
 .
. - "Flight without Bernoulli" Chris Waltham Vol. 36, Nov. 1998 The Physics Teacher – using a physical model based on Newton’s second law, the author presents a rigorous fluid dynamical treatment of flight. [1]
- Bernoulli, Newton, and Dynamic Lift Norman F. Smith School Science and Mathematics vol 73 Part I: [2] Part II [3]
Спољашње везе[уреди | уреди извор]
- NASA tutorial, with animation, describing lift
- Explanation of Lift with animation of fluid flow around an airfoil
- A treatment of why and how wings generate lift that focuses on pressure.
- Physics of Flight - reviewed. Online paper by Prof. Dr. Klaus Weltner. Архивирано на сајту Wayback Machine (9. март 2021)
- Explanation of Lift with animation of flow around an airfoil.
- How do Wings Work? - Holger Babinsk
- Симулација опструјавања аеропрофила Архивирано на сајту Wayback Machine (27. април 2014)

























