Бернулијева једначина

Струјна цев променљивог попречног

пресека, кроз коју протиче флуид.

Бернулијева једначина је једна од основних математичких дефиниција, у делу физике, која се зове динамика флуида. Описује Бернулијев принцип, односно дефинише међусобну везу између притиска или потенцијалне енергије флуида и његове брзине или његове кинетичке енергије, у струјној цеви (струјном пољу). Бернулијев принцип је добио име по данско-швајцарском научнику Данијелу Бернулију, који је описао овај принцип у својој књизи Hidrodinamica 1738. године. Бернулијева једначина служи управо за описивање овог принципа и израчунавање параметара везаних за проток флуида.

Постоји више облика Бернулијве једначине које описују разне врсте протока флуида. Најједноставнији облик Бернулијеве једначине се односи на случај када се густина флуида може узети као непроменљива (код течности и код занемаривања стишљивости гаса на малим брзинама). Постоји и једначина за проток флуида када се густина не може узети као константна. Код већих брзина гасова, када се мора узимати у обзир њихова стишљивост, тада се уводи у једначину Махов број, као еквивалент брзине. Бернулијева једначина се додатно усложњава ако се ради о вискозном струјању.

Бернулијев принцип се може извести из закона о одржању енергије. Наиме, из овог закона следи да у мирном току флуида сума свих облика механичких енергија, у целом струјном току, мора бити једнака у свима тачкама тога поља. Другим речима, сума кинетичке и потенцијалне енергије мора бити међусобно једнака у свима тачкама струјног поља.

Честице флуида су под утицајем сопствене тежине и притиска, крећу се између тачака са различитим статичким притиском, од већег према мањем. Ако се флуид креће хоризонтално, кроз струјну цев, брзина ће се повећавати ако се та разлика статичког притиска повећава између две тачке, односно између два пресека цеви. Брзина флуида се смањује ако се та разлика статичког притиска смањује. Највећа брзина је тамо где је притисак најмањи, а најмања је тамо где је притисак највећи.

Проток нестишљивих флуида

Дејство сила на делић флуида, у струјном пољу.

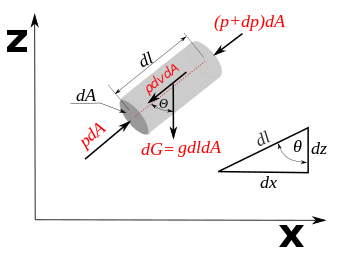
У случају већине течности, и гасова са малим маховим бројем, густина флуида се може сматрати константном (одатле ‘’нестишљивих’’), без обзира на варијације у притиску. У овом случају Бернулијева једначина има облик:

${v^2 \over 2}+gz+{p\over\rho}=\text{const}$

Где је:

$v\,$ је Брзина протока у некој тачки тока,

$g\,$ је гравитационо убрзање,

$z\,$ је висина по z-оси(позитиван део z-осе је усмерен према горе, дакле супротно од смера деловања гравитације)

$p\,$ је притисак, и

$\rho\,$ је густина флуида у свим тачкама флуида.

Важне напомене:

• флуид мора бити нестишљив-упркос промењивом притиску, густина мора остати иста да би једначина важила
• Овај облик Бернулијеве једначине важи за случај када су вискозне силе занемарљиве

Ако се горња једначина помножи са густином добија се следећа једначина:

$\tfrac12\, \rho\, v^2\, +\, \rho\, g\, z\, +\, p\, =\, \text{const}\,$

или:

$q\, +\, \rho\, g\, h\, =\, p_0\, +\, \rho\, g\, z\, =\, \text{const},$

Где је:

$q\, =\, \tfrac12\, \rho\, v^2$ динамички притисак.

У поједностављеном посматрању (поготово ако је флуид гас), притисак је услед тежине стуба флуида у посматраном малом делићу, занемарљиво је мали. На основу тога је реално усвојити: ρ gz = 0. Тада Бернулијева једначина добија једноставнији облик:

$\ p + \frac {\rho\,\ v^2 }{2} =\, \text{constant}\,\quad \longmapsto \quad \ p + \ q =\, \text{const}\,$

Збир статичког и динамичког притиска у свим тачкама струјне цеви је константан број. Ова једначина се још назива и једначином о одржању енергије.

Проток стишљивих флуида

Горње једначине важе за нестишљиве флуиде, међутим могуће је, користећи фундаменталне физичке законе, доћи до једначина који су сличне њима али су примењиве и на стишљиве (бароторопне) флуиде. Постоји много облика Бернулијеве једначине и све су оне аналогне основној Бернулијевој једначини и ослањају се на фундаменталне законе попут Њутнових закона и првог закона термодинамике. Једна од најчешће коришћених једначина за стишљиве флуиде је:

$\frac {v^2}{2}+ \int_{p_1}^p \frac {d\tilde{p}}{\rho(\tilde{p})}\ + \Psi = \text{const}$

Где је:

p притисак

ρ густина течности

v брзина протока

Ψ гравитациони потенцијал.

Види још

• Термодинамика
• Аеродинамика
• Динамика флуида

Спољашње везе

• О кретању флуида

Викимедијина остава има још мултимедијалних датотека везаних за: Бернулијева једначина