Аеродинамика

Аеродинамика (од грч. ἀηρ, aēr, aéros — ваздух, и δύναμις, dynamis — сила) је наука која се бави кретањем ваздуха у односу на чврста тела. Физикалност је потпуно идентична и у супротном случају, при кретању чврстих тела кроз ваздух. Према томе примењеном принципу, релативног кретања, анализа феномена се изводи аналогно случају када тело мирује у струјном пољу ваздуха. Ова замена референтног стања је усвојена у теоријској аеродинамици, али је она уједно и основа већине експерименталних метода, нарочито за испитивања у аеротунелима.
Теорија струјања и физикалност кретања чврстих тела изучавају међусобно дејство флуида и тела. То дејство се одређује у облику потенцијала поља опструјавања, расподеле притиска, сила и момената њиховог међусобног дејства.
Земљина атмосфера представља ваздушни омотач око Земљине кугле. На основу усвојених дефиниција, тај ваздушни омотач се дели на четири слоја. Почев од Земљине површине па навише, слојеви су: тропосфера, стратосфера, јоносфера и ексосфера (која представља границу с међупланетарним простором). Атмосферу карактеришу промене физичких величина притиска, температуре, влажности, густине итд. у функцији висине, годишњег доба и географске ширине и дужине. Усвојене статистичке средње вредности физичких величина су стандардизоване, међународним нормама, у стандард атмосферу. Измерене карактеристике кретања тела кроз ваздух, при конкретним атмосферским условима, се преводе на те услове стандард атмосфере и тако постају референтне за поређење, при анализама.
Шире гледано, кретање тела кроз гасове и течност се изучава у механици флуида

(енгл. John D. Anderson).[1][а]
Подела аеродинамике, као специфичне гране науке, врши се на више начина, с неколико основа. Поједини аеродинамички проблеми се истовремено решавају у више њених грана. Пример је одређивање и коришћење отпора ваздуха. Припада свима деловима, добијеним при подели аеродинамике. Отпор се одређује аналитички и експериментално у свим областима брзина, висина и услова лета и присутан је у свим разматрањима. Припада свима деловима, добијеним при подели аеродинамике. Отпор се одређује аналитички и експериментално у свим областима брзина, висина и услова лета и присутан је у свим разматрањима. Начин поделе аеродинамике може да варира, зависно од искуства и ставова аутора, значи није строго стандардизован. Прилази аутора, у начинима поделе аеродинамике, ипак су међусобно доста слични.
Основе објашњења аеродинамике датирају од Аристотела и Архимеда, у 2. и 3. веку пре нове ере,[2] али развој квантитативне теорије протока ваздуха је почела тек у 18. веку. У 1726. години, Исак Њутн је постао један од утемељивача напредне аеродинамике.[3] Већина раних истраживања у аеродинамици одвијала су се у правцу решења проблема да тело теже од ваздуха лети, што су први демонстрирали браћа Рајт 1903. године. Од тада, је решавана употреба аеродинамике кроз математичке анализе, емпиријске апроксимације, експерименте у аеротунелима, експериментисањем и компјутерским симулацијама је формирана научна основа за кретање тела тежег од ваздуха у облику лета и низа других технологија. Најновији рад у аеродинамици је фокусиран на питања везана за стишљивост током протока, турбуленцију и гранични слој, а ти феномени постају све више рачунски обрадиви.[4]

Утицај брзине, густине и температуре ваздуха на аеродинамичке феномене[уреди | уреди извор]

Лет савремених авиона, сателита и космичких летелица, прошириле су област аеродинамике, до крајњих граница. Специфичности феномена, у оквиру тих граница, основа су за њену поделу и проучавања.[4][5]
Основе аеродинамике[уреди | уреди извор]
Класична аеродинамика изучава део у којем се, већим делом, сматра да је ваздух идеалан флуид. То подразумева да је ваздух потпуно безвискозан, али може бити стишљив и нестишљив. Безвискозност значи да нема тангенцијалног напона између честица ваздуха при њиховом кретању, а ни у односу на површину тела, коју опструјава. Занемаривање вискозности, у одређеном опсегу брзина и висина је допустиво и корисно, за аналитичко изучавање већине феномена у аеродинамици. Реалан ваздух је вискозан и он се, у неким случајевима аналитички обавезно узима у обзир, нпр. при одређивању граничног слоја.
Струјање ваздуха се, у основи, енергетски дефинише с једначинама континуитета и Бернулија.
Посматрајући проток ваздуха, као идеалног флуида, у јединици времена кроз пресеке струјне цеви (1) и (2), добија се:[6][7]
| Ово је једначина континуитета или другачије речено закон о одржању масе: | Где су: |
При струјању ваздуха с малим брзинама, преноси се слаб поремећај између његових честица, готово без измене њиховог растојања. У таквим условима се сматра да је ваздух нестишљив, па је ρ1 = ρ2. Тада једначина континуитета добија једноставан облик:

При усвојеном појму нестишљивог флуида, кретање гасова и течности се разматра на исти начин и не прави се разлика међу њима.
Применом принципа Даламбера, на посматрани мали цилиндрични елеменат флуида дужине dl и константне површине попречног пресека dA добија се једначина кретања:[7][8][9]
На основу скице је очигледна једнакост: dz = dl cos θ. Сређивањем и интегрирањем, једначина кретања добија облик:[9]
Где су:
|
Очигледно да је притисак, услед тежине ваздушног стуба у посматраном малом делићу ваздуха, занемарљиво мали. На основу тога је реално усвојити: ρ g z = 0. Тада једначина Бернулија добија облик:
Збир статичког и динамичког притиска у свим тачкама струјне цеви је константан број. Ова једначина се још назива и једначином о одржању енергије.[8][9]
Увођење у разматрање стишљивости, термодинамичких и других утицаја, усложњава изглед једначина континуитета и Бернулија.
Класична аеродинамика се дели према специфичностима утицаја брзина струјања на стишљивост ваздуха. Те области су одређене интензитетом брзина струјања, поређеним с брзинама ширења звука кроз ваздух. За брзину тела: мању од брзине звука, приближно исту и изнад брзине звука.
Брзина тела, при кретању кроз ваздух (исто, као и брзина ваздуха у односу на тело) је , а брзина звука је . По професору физике Ернесту Маху,[10] уведен је однос брзине лета и брзине звука, као бездимензиони број. Користи се за везу утицаја стишљивости ваздуха на аеродинамичке величине.[11][12]
| Математичка дефиниција Маховог броја: |
Подзвучна (супсонична) аеродинамика[уреди | уреди извор]
Ова област аеродинамике проучава ваздушно струјање у коме у прорачунима може да се занемари утицај стишљивости. Искуствено је та граница постављена до брзина струјања ваздуха близу M = 0,8.
Под кретањем ваздуха се подразумева кретање његових честица, већих од молекула. Путања сваке честице ваздуха представља струјницу. Струјница се може визуелно приказати и уочити ако се убаци дим у ваздух који струји у аеротунелу. Овако дефинисане струјнице ваздуха, опструјавају тело које се креће, у правилном распореду, без промене међусобног растојања при раванском, униформном струјању. Ово поједностављење служи за елементарну математичку дефиницију (симулацију) струјања. При томе се користе једначине Бернулија и континуитета, у претходном поједностављеном облику, с прихватљивом тачношћу. Струјање се реалније моделира ако се посматра просторно (у три димензије), ако се не занемарује вртложење (ротирање честица дуж струјнице) и ако се узима у обзир утицај вискозности на формирање граничног слоја.
Са развојем теоријске аеродинамике, информатичких технологија и нумеричких метода све је мање уведених апроксимација у математичку дефиницију, те су и прорачуни реалнији. С тиме се веродостојније осликава физикалност струјања.[4][13]
Крозвучна (транссонична) аеродинамика[уреди | уреди извор]
Овај део аеродинамике изучава струјање ваздуха у прелазном распону брзина од подзвучних до надзвучних. Грубо је искуствено дефинисан у распону: 0,8 < M < 1,4.
Када се тело креће кроз ваздух, сигнал о његовом присуству се преноси преко честица ваздуха, с једне на следећу, дуж струјнице, брзином звука. При кретању с мањим брзинама, од брзине звука, честице ваздуха имају времена да изменом облика своје путање заобилазе тело, задржавајући тако своје првобитно међусобно растојање и после сигнализиране принуде од присуства тела. При томе се сматра да у струјном пољу, око тела, густина ваздуха остаје иста (нестишљиво струјање). Када је брзина тела већа од брзине звука, при кретању кроз ваздух, његове честице се сударе с телом пре него што стигне сигнал до њих о присуству истог. Тело, при кретању у тим условима, гура честице ваздуха с њихове путање. То ствара грубу принуду и међусобно померање честица ваздуха у струјном пољу, што се даље простире у облику таласа.
У крозвучној области брзина, успостављају се појединачни локални ударни таласи, те нису применљиве методе прорачуна ни за подзвучну нити за надзвучну аеродинамику. У овој области брзина су компликовани аеродинамички прорачуни, приближне тачности, што увек захтева детаљну експерименталну потврду. Режим лета летелица се не задржава дуже, у овој области брзина. Оперативни режими лета летелица су изван тих брзина. То је пролазна област за лет на надзвучним брзинама.[14]

Надзвучна (суперсонична) аеродинамика[уреди | уреди извор]
Ова област аеродинамике је искуствено одређена да важи за распон брзина 1,4 < M < 6.
Струјно поље је с надзвучним брзинама, то јест с косим ударним таласима. С повећањем надзвучних брзина, тела кроз ваздух, повећава се и нагиб косог ударног таласа. Пример је приказан на слици. Дуж граничне линије таласа, преноси се та принуда поремећаја и она је уједно и граница различитог нивоа притиска. Иза ње је нагла промена. После линије предњег је скок, а иза линије задњег ударног таласа је пад притиска (експанзивни талас). Гранична линија таласа се назива Махова линија. У случају тачкастог поремећаја, ствара се Махов конус, чији се полуугао ψ, може одредити математичким релацијама:[12]
Карактеристичан је случај тачкастог поремећаја с брзином, једнаком брзини звука , тада је:
Тада је Махов талас у облику нормалног ударног таласа. Пролазак летелице кроз тај режим, лаички се назива пробијање звучног зида, што је праћено звуком експлозије, због тренутног скока притиска.[12]

Хиперсонична аеродинамика[уреди | уреди извор]

Ову област карактеришу велике брзине, које одговарају бројевима Маха од M ≥ 6. На овим великим брзинама су ударни таласи веома интензивни. У неким случајевима долази и до електро-хемијских промена у ваздушном струјном пољу. Ваздух потпуно престаје да се понаша по законима идеалног (савршеног) гаса. У тим условима брзина, ваздух се мора третирати као реалан гас. Појављују се феномени дисоцијације и јонизације. Поготово су присутне ове појаве у горњим слојевима атмосфере (јоносфера > 80 km), где је ваздух већ добрим делом јонизован. Аеродинамичка истраживања ових феномена се одвијају, првенствено, у одговарајућим аеротунелима. Ове инсталације постоје са симулацијом само великих брзина, а и с реалнијим условима у којима се истовремено симулирају и високе температуре, које прате феномене хиперсоничне аеродинамике. На слици је приказан лабораторијски хиперсонични аеротунел, без симулације високих температура. Инсталиран је у ВТИ-у, Жарково.[15][16]
Аеродинамика слободних молекула[уреди | уреди извор]
На великим висинама, апсолутни притисак ваздуха је драстично умањен а с њиме и густина. Проток који има веома малу густину не може се моделирати коришћењем претпоставке континуума.
У овом случају, свака честица мора бити моделирана засебно. Ако је густина довољно мала, судари између честица могу игнорисати. Без судара, честице не магу утицати једна на другу и међусобно се могу моделирати као независне учеснице у протоку. Ови доприноси се могу сумирати за расподелу притиска и узгона на телу, које се креће кроз ту средину. Сагласно овоме, средњи пут молекула је реда величина тела које се креће кроз ту ваздушну средину. У таквом кретању се молекули ваздуха (гаса) понашају као пројектили који бомбардују површину тела. У оваквим условима је класична аеродинамика, континуалних средина, немоћна. Овде се користе друге методе и технике за прорачуне.[17]
Магнето-аеродинамика[уреди | уреди извор]
При лету у јоносфери са хиперсоничним брзинама, иза одвојеног ударног таласа, на предњем делу тела, постижу се температуре око 10.000 °C. У овим условима, прегрејаног и јонизованог ваздуха јаке електричне проводљивости, појављује се феномен дисоцијације ваздуха. Теоријске и експерименталне методе, у овој области, се преплићу с технологијама акцелератора, плазме и плазма мотора.
Оживљавање истраживања у области магнетне-аеродинамике је изложен многим тешкоћама за брзи развој интердисциплинарних потреба, али показује индикације да постаје нова техничка препрека. Ова дисциплина подмлађена, потпомогнута модерном рачунарском техником и експерименталним иновацијама, открива потенцијал да обезбеди нову димензију за побољшање перформанси летелица. Комбинујући технологију развоја електромагнетике, аеродинамике, као и хемијске кинетике може довести до мултидисциплинарног продора у ваздухопловној науци. Најновија теоријска, рачунарска, и експериментална истраживања у магнетној-аеродинамици подржавају напоре истраживања и синергизам.[18]
Не-Њутнова струјања[уреди | уреди извор]
У питању је струјање вискозног гаса. Њутново струјање подразумева линеарну зависност тангенцијалног напона и градијента међусобне брзине честица гаса. Тај градијент представља константну вискозност. Код не-Њутновог струјања вискозност расте у функцији односа вредности тангенционалног напона и градијента међусобне брзине честица гаса. Ово струјање се зове високо еластично. Постоје и неки пластични флуиди, код којих, после одређених вредности односа тангенционалног напона и градијента брзина, вискозност почне да опада.[19]
Методе истраживања и развоја[уреди | уреди извор]
У аеродинамици се користе аналитичке и експерименталне методе истраживања и развоја. Оне се међусобно преплићу, допуњују и испомажу. Међусобна доминација и предност, ових метода, зависи од врсте проблема у истраживању.
Ова основа за поделу се односи на целу аеродинамику, односно на све њене сегменте.
Прорачунска аеродинамика[уреди | уреди извор]

Аеродинамика је напредовала с развојем механике флуида, термодинамике, нумеричких метода и информатичке технологије. Развијене су снажне методе математичке симулације струјања ваздуха у свим условима, брзине, густине и температуре, с пратећим феноменима. Коришћене су методе и радови: Исака Њутна, Жан д'Аламбера, Жозефа Лагранжа, Пјера Симона Лапласа, Лудвига Прантла, Николаја Жуковског, Теодора фон Кармана, Ериха Трефца, Клода Навјеа, Габријела Стокса, Леонарда Ојлера и других. Пример, у ближој прошлости конструктори авиона су пројектовали аеродинамику крила и подешавали његов спољни облик, сложеним методама приближавања, првенствено користећи парцијалне експерименталне податке. Сада се аеродинамички пројекат крила ради аналитички, помоћу Ојлерових кодова и других ефикасних алата, за задате почетне услове и строге критеријуме оптимизације.
Илустрација аналитичког одређивања и визуелизације расподеле притиска је приказана на слици. Врста боје одговара нивоу притиска, тамноплава најнижем а тамнонаранџаста највишем. Поклапање резултата, са измереним у аеротунелу, је одлично.
У прошлости је један од првих и приоритетнијих задатака нумеричке аеродинамике био изналажење методологије прорачуна аеродинамичке силе, која делује на тело при његовом кретању кроз ваздух. Аеродинамичка сила је последица разлике притиска, због циркулације око несиметричног тела, и утицаја вискозности (трења) ваздуха. Тај утицај се може написати као симболична функција утицајних физичких величина:[10][20]
| Где су: |
Математичким трансформацијама и димензионом анализом, претходне функције, добија се једначина облика:
Сагласно, да је у једначини Бернулија дефинисан динамички притисак, који се у аеродинамици обележава .
Где је , бездимензиони коефицијент аеродинамичке силе. Константан је у области брзина где се може занемарити утицај стишљивости и где је обезбеђена сличност слике опструјавања.
Уобичајено је да се укупна аеродинамичка сила обележава с ,
У принципу, за реалан гас, што је фактички и ваздух, је функција броја Маха због утицаја стишљивости и броја Рејнолдса због утицаја различитости слике опструјавања, што је последица вискозности ваздуха.[21]
Рејнолдсов број је без димензије. Уведен је у бездимензионој анализи и трансформацији опште једначине за аеродинамичку силу, као веза утицајних величина:[22]
Где је , референтна дужина која карактерише величину тела које се креће кроз ваздух. Код авиона се усваја средња аеродинамичка тетива а код ракета пречник трупа.
Аеродинамичка сила делује на неком краку у односу на тежиште тела и на тај начин ствара момент. Резултујући аеродинамички момент је једнак производу аеродинамичке силе и њеног крака до тежишта тела. У бездимензионој анализи за момент се појављује све исто као за аеродинамичку силу, плус референтна дужина, због бездимензионисања крака момента. Референтна дужина , је већ дефинисана у броју .
Израз за резултујући аеродинамички момент је у облику:
Аеродинамичка сила, па и аеродинамички момент, се мењају с положајем тела у односу на правац и брзину струјања ваздуха. Померањем тежишта тела може се пронаћи тачка, у којој се момент не мења без обзира на промену интензитета аеродинамичке силе. Када тело није симетрично, постоји момент сталног интензитета, у односу на ту тачку, независно од вредности аеродинамичке силе, чак и при њеном интензитету једнаком нули. То значи да та тачка лежи на правцу дејства аеродинамичке силе, а постојећи момент константног интензитета је спрег сила, последица несиметричне расподеле притиска. За случај симетричног тела момент ће увек бити једнак нули, у односу на ту тачку, без обзира на интензитет аеродинамичке силе. Та се тачка на телу, назива аеродинамички центар. Резултујући аеродинамички момент, у односу на аеродинамички центар је:
Према дефиницији, да је при резултујућој аеродинамичкој сили једнакој нули, или при њеном краку једнаком нули и на основу линеарне зависности момента од силе, израз за коефицијенат укупног аеродинамичког момента има облик за било који положај тежишта, изван аеродинамичког центра:
Где је , је бездимензиони број, који представља ефекат крака аеродинамичке силе у односу на тежиште тела.[20]


Експериментална аеродинамика[уреди | уреди извор]
Бави се мерењем аеродинамичких параметара и карактеристика.
У аеротунелима[уреди | уреди извор]
Аеродинамички тунели су наменске инсталације за физичку симулацију ваздушног струјања око модела тела, на коме се врше аеродинамичка мерења. Модел је верна копија облика и димензија тела у размери, коју диктира величина радног дела аеротунела.
Модел се уграђује у радни део аеротунела преко мерних уређаја (аеровага), које региструју податке о његовим аеродинамичким оптерећењима, за разне услове опструјавања. Аероваге су некада биле механичке (кинематске) а сада су електронске. Према начину интеграције с моделом, могу бити спољне и унутрашње. Унутрашње се уграђују у тело модела (код авиона у труп). Према могућностима мерења могу, истовремено, мерити више компонената. На пример, шестокомпонентне мере све три силе и сва три момента истовремено. Поред мерења аеродинамичких сила, момената и дериватива стабилности, у аеротунелима се мери и расподела притиска по додирној површини модела с ваздухом а остварује се и фотографише и визуелизација струјног поља.
У аеротунелима се тешко може остварити сличност са стварним условима кретања тела кроз ваздух. Зато се, у случајевима већих разлика, врши корекција резултата, за различиту стишљивост, преко броја Маха, a у случају различите слике опструјавања, с бројем Рејнолдса. Посебно је тешко у аеротунелима постићи Рејнолдсов број истог реда величина као у стварним условима лета, на пример за авион. Практично не постоји радни део аеротунела толиких димензија да може прихватити модел авиона у размери 1:1. То значајно умањује број Re преко смањеног la (с размером), чак и за исту брзину струјања ваздуха. Веома је тешко остварити велики радни део аеротунела (за прихват великих модела) с великим брзинама струјања ваздуха. Кроз компромис се жртвује једно или друго, а најчешће, у некој мери, обоје.
У Србији су изграђени аеротунели и у оперативној су употреби у ВТИ-у, Жарково и на Машинском факултету, ваздухопловном одсеку, у Београду.[23][24]
У лету[уреди | уреди извор]
Испитивања и мерења у лету се првенствено врше у сврху верификације остварених летних карактеристика летелице и њиховог одступања од тактичко-техничких захтева (ТТЗ-а). У оквиру тог процеса се посредно одређују аеродинамичке карактеристике. У току развоја летелице, аналитички и аеротунелски се одређују аеродинамичке карактеристике с којима се прорачунавају летне карактеристике. У лету се мере остварене летне карактеристике и на основу познатих карактеристика погона, масе и инерцијалних момената летелице прорачунски се одређују њене аеродинамичке карактеристике. На овај начин је створена основа за међусобно упоређивање и корекцију свих примењених метода истраживања и мерења у аеродинамици.
Поред верификационих, раде се и наменска истраживачка и развојна испитивања. На пример интеграцијом подвесног терета, преко аероваге, могу се у лету мерити аеродинамички параметри. На томе принципу, може већа, носити мању летелицу или њен модел ради мерења аеродинамичких карактеристика у условима стварног лета. Последњих двадесетак година су коришћени серијски авиони као летеће лабораторије, у сврху испитивања појединих сегмената нових технологија. На те серијске авионе, уграђиване су нпр. електричне команде лета (FLY-BY-WIRE) и истраживани су сви аспекти, посебно стабилност и управљивост, за примену у наредним, новим пројектима.[25][26]
Испитивања, истраживања и мерења у лету се врше у Србији у Ваздухопловноопитном центру.
Примењена аеродинамика у пројектовању летелица[уреди | уреди извор]

Ова подела се односи на групе сродних задатака у пројектима летелица, првенствено авиона.
За анализу опструјавања и за одређивање аеродинамичких сила и расподеле притиска тело се третира као безматеријално са стриктним обликом и геометријом оквашене површине. За одређивање аеродинамичког момента исто то, с тим што се одреди тачка у односу на коју се момент односи. При прорачуну перформанси и еволуција, летелица се замењује с материјалном тачком. За ковит се, у прорачуну, користе и моменти инерције летелице. При анализи и синтези динамичке стабилности, летелица се третира као реално тело, са својом геометријом, масом и моментима инерције.[27][28]
Општа аеродинамика[уреди | уреди извор]

Општа аеродинамика се бави дефиницијом аеродинамичких карактеристика, коефицијената аеродинамичких сила и момената летелица, познатог облика и геометрије. У оквиру ове групе задатака, првенствено се подешава облик и геометрија летелица у циљу побољшања опструјавања и постизања њених бољих аеродинамичких карактеристика.
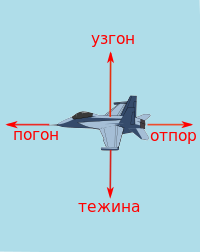
За решавање конкретних задатака, у оквиру пројектовања летелица, није интерес одређивање укупне аеродинамичке силе и момента, већ њихових компонената. Узгон Rz је компонента укупне аеродинамичке силе, нормална на правац брзине кретања. Отпор Rx је компонента у правцу кретања.[27][29] Компонента укупног аеродинамичког момента, која делује око бочне осе, нормалне на правац брзине и на правац узгона, назива се момент пропињања My. Сагласно дефиницији укупне аеродинамичке силе и момента, њихове компоненте се могу написати у облику:[27][28]

Коефицијенти компонената аеродинамичке силе и момента, у општем случају, су функције од нападног угла α, облика тела и бројева Маха (M ) и Рејолдса (Re ) :
Узгон летелице је корисна компонента аеродинамичке силе. Отпор је нежељена неповољност. Упрошћено речено, задатак се своди на минимизацију отпора при постизању потребног узгона. Узгон се остварује с узгонским површинама (крилима), које се уграђују на летелицу за ту функцију.[30] Пресеком крила с равни, паралелном с равни симетрије летелице, добија се аеропрофил. Избором контуре аеропрофила и облика крила утиче се на величину и међусобни однос узгона и отпора истог, за различите услове опструјавања. При томе процесу оптимизације, поред нумеричких метода, користе се и експериментални подаци и експериментална провера остварених решења. Експериментални аеродинамички подаци се најчешће односе за нижи ред величина броја Рејнолдса, у односу на реалне услове лета. Ређи је то случај с Маховим бројем. По потреби се врши поправка података, с бројевима Re и M.
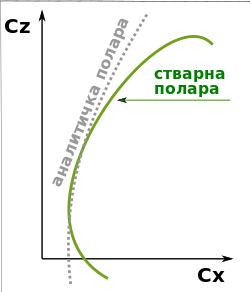
Узгон је у линеарној зависности од нападног угла, све до близу . На нападним угловима, близу критичног, опструјавање није око целог тела (аеропрофила), регуларно. У тим условима ваздушне струјнице не могу стриктно пратити контуру аеропрофила и одвајају (отцепљују) се. Тада престаје линеарна зависност узгона од нападног угла и при даљем повећању истог прираст узгона слаби. Нагло узгон пада на критичном нападном углу (као на приказаном дијаграму). Летелица се не сме довести у тај режим, осим у намерно превученом лету. Највећа постигнута вредност узгона је , односно његов коефицијент се постиже на критичном нападном углу .[31] За исти облик тела при кретању кроз ваздух, мањи је при мањим бројевима Re. Зато се експериментални податак за узгон, из аеротунела, обично измерен при мањем Re, коригује формулом:[32]
Где су индекси 1 у лету а 2 у аеротунелу.
Експонент се аналитички одређује, на основу резултата неколико мерења узгона на различитим бројевима Re.
Отпор се коригује с бројем Re због различитог утицаја вискозности (трења), транслацијом целе криве преко измене његове минималне вредности. Као пример, за узгонске површине се користи корекција:[32]
Квалитетна процена отпора тела (летелице) је основни предуслов за прорачун перформанси лета. Због тога се узимају у процену и прорачун сви утицајни чиниоци, односно доприноси.[33][34]
- Отпор облика, не би постојао да је ваздух стварно невискозан и нестишљив. Тада не би постојала разлика притиска испред и иза тела. Ово уједно говори и о ограничењима примене принципа Даламбера.
- Површинско трење, је допринос услед вискозности ваздуха и стварања трења између честица у граничном слоју, где се честице успоравају интензивније што су ближе површини тела.
- Отпор аеропрофила, је збир два претходна доприноса за дводимензионално струјање.
- Индуковани отпор је допринос утицаја тродимензионалног опструјавања, услед коначног размаха крила летелице. Услед разлике притиска изнад и испод крила, бочно се прелива ваздух с доње на горњу страну, стварајући слободне вртлоге (види се на слици десно). Појављује се само при узгону крила и управном је пропорционалан његовом интензитету. Када се дода овај утицај на претходни отпор аеропрофила, добија се збирни отпор крила, који садржи утицај облика, допринос површинског трења и индукованог отпора.
- Паразитни отпор, је онај који није последица стварања узгона. То су отпор трупа, отпор разних гондола итд.
- Отпор интерференције, је допринос међусобног утицаја близине аеродинамичких тела.
- Таласни отпор, је последица појаве ударних таласа.
- Отпор услед хлађења мотора, се појављује због губитка енергије ваздушних струјница при проласку кроз хладњаке и друга места одвођења топлоте.
Отпор се мења, с променом нападног угла, по приближно параболичној функцији. У близини критичног нападног угла брже расте, а после њега драстично. То је посебно сликовито, ако се прикаже међусобна зависност узгона и отпора. Та међусобна зависност узгона и отпора, графички и аналитички приказана, се назива полара. Она је од кључног значаја за аеродинамичко пројектовање летелица, посебно за одређивање перформанси. Свака тачка на полари се односи на одређени режим лета, с одређеним нападним углом. Могућа је приближна аналитичка дефиниција поларе, с применом начелног, почетног прилаза:
У прорачунима, у завршним фазама развоја пројекта, користи се реалнија, такозвана равнотежна полара. У равнотежној полари је придодат и прираст отпора услед отклоњених командних површина за уравнотежавање летелице, за дотични режим лета.[35]
 |

|

Механика лета[уреди | уреди извор]
Механика лета се односи на сву практичну проблематику карактеристика лета, у процесу развоја и оперативне употребе авиона. Начелно, обухвата перформансе, маневарски лет, превучени лет, стабилност и управљивост. Овде су енциклопедијски дате само неке од елементарних поставки прорачуна, у оквиру те проблематике.
Перформансе[уреди | уреди извор]
- Стационарни режим лета
- Минимална и максимална брзина хоризонталног лета
- Перформансе пењања
- Специјалне перформансе
- Полетање
- Слетање
- Долет и трајање лета
- Перформансе у маневарском лету
- Планирање
- Обрушавање
- Заокрет
- Стационарни
- Нестацоинарни
- Еволуције
- Нагло пењање
- Петља
- Имелман
- Борбени заокрет
- Превртање
- Ваљак
- Ковит[36]
Стационарни хоризонтални и лет у пењању, подразумева равнотежу свих сила које делују на авион при константној брзини.
| Хоризонтални лет дефинишу једначине: | |
| 1) | Где су: |
| 2) |




Трансформацијом се, из претходних једначина, добија потребна брзина за одржање хоризонталног лета, на заданом нападном углу:
У случају занемаривања угла између правца потиска и брзине лета, израз за брзину се поједностављује:
Режим минималне брзине одговара условима лета у првој пресечној тачки дијаграма потребне и расположиве снаге.
У пењању:
Где је , угао између хоризонтале и правца путање лета.
У условима стационарног пењања, нагиб путање је у релацији , при чему се може сматрати . На основу овога се добија, из друге једначине, исти израз за брзину на путањи као у хоризонталном лету.
Множењем прве једначине са брзином , добија се израз за вертикалну брзину пењања:
Где је:
|
Максимална брзина се одређује из услова одређивања режима стационарног хоризонталног лета , у коме се поклапа потребна и расположива максимална снага. Тај режим лета је у другој тачки пресека, на дијаграму потребна и расположива снага.
Ово су примери полазних поставки прорачуна једноставнијих перформанси, са прихватљивим упрошћењима. Сличан прилаз је и за прорачун осталих.
Без обзира што је, у прошлости, прорачун перформанси авиона на овај начин давао задовољавајуће резултате, сада постоји велика количина направљеног софтвера за прецизније њихово одређивање, без апроксимација.[37]
Превучени лет[уреди | уреди извор]
Лет авиона с нападним углом,назива се превучени лет. Већ је речено да се минимална брзина, у стационарном хоризонталном лету, постиже при . Даљим повећањем нападног угла, узгон нагло пада, с чиме престаје и регуларни лет. Тада авион пада у ковит. На левом и десном крилу, најчешће, несиметрично се губи узгон. Та асиметрија изазива ротацију авиона око све три осе.[38]

Стабилност и управљивост[уреди | уреди извор]
Авион може да промени свој правац кретања на неколико начина. Пре свега, да се креће нагоре или спушта доле. Ово се постиже променом узгона на хоризонталном репу, преко отклањања његовог крмила. Следеће је ваљање стварањем асиметрије узгона крила, преко отклона крилаца, која се диференцијално отклањају као део излазне ивице крајева крила. Такође и скретање с правца помоћу крмила правца, које се налази на вертикалном репу авиона. Ове командне површине су интегрисане у систему команди лета авиона.[39]
Раван симетрије дели авион на два, пресликана, дела (леви и десни). Симетрични лет авиона је без бочног нагиба и без клизања. Тада се вектор брзине лета поклапа с равни симетрије авиона. У таквом симетричном кретању је симетрична и расподела притиска, на левој и десној страни авиона. На основу тога, аеродинамичке силе и момент делују у равни симетрије авиона. Ово је тако звано уздужно кретање авиона. У проблематици стабилности се разматра издвојено, пошто не изазива појаву бочне силе и моменте ваљања и скретања. Стабилност у уздужном кретању се назива уздужна стабилност.
Ваљање и скретање авиона су у међусобној зависности („куплују“ се). У томе кретању се разматра попречно-смерна стабилност. При томе кретању вектор брзине није у равни симетрије авиона, с њом заклапа угао клизања . Угао β изазива појаву бочне силе Ry, момент ваљања Mx и момент скретања Mz, као што нападни угао изазива силу узгона Rz, силу отпора Rx и момент пропињања My.


За разјашњење проблематике стабилности сваког тела, па и авиона, потребно је објаснити појам поремећаја. То је принуда, која авион изводи из равнотежног стања. Та принуда може бити услед управљања авионом, од стране пилота, услед одбацивања терета, удара ветра итд.[40][41]
Статичка стабилност[уреди | уреди извор]
Статичка стабилност изучава равнотежу сила и момената, који делују на авион, пре и после поремећаја стања мировања. При томе се не узимају у обзир силе и моменти у функцији времена. Статички је стабилан авион, када га прираст аеродинамичких сила и момената, изазван с поремећајем, враћа у претходни положај. Статички је нестабилан авион када га прираштај аеродинамичких сила и момената, изазван поремећајем, удаљава од почетног стања. Статички је неутралан авион код кога поремећај не изазива никакве прираштаје аеродинамичких момената.
На основу теорије линеарности, у домену малих поремећаја, могу се одвојено разматрати уздужна и попречно-смерна статичка стабилност. Прилази су слични, заснивају се на услову равнотеже аеродинамичких сила и момената.
Уздужна статичка стабилност се решава с полазном поставком равнотеже аеродинамичког момента пропињања авиона, добијеног сабирањем појединачних доприноса делова авиона.[41][42][43]
Уздужна равнотежа авиона, одговара пресечној тачки између линеарне функције и апсцисе (погледајте дијаграм).
Где су скраћенице:
|
|
Сасвим је довољно, за илустрацију, приказати као пример, само принцип одређивања статичке стабилности с једноставним моделом доприноса од узгона крила и хоризонталног, репа на уздужну равнотежу авиона.[тражи се извор]
Где је:
- – апсолутна удаљеност између тежишта авиона до аеродинамичког центра крила. Дељењем ове величине с la добија се бездимензионо релативно растојање, припремљено за коришћење у бездимензионој једначини уздужне равнотеже.
- – апсолутна удаљеност између тежишта авиона и аеродинамичког центра хоризонталног репа
- – волумен хоризонталног репа
- – ефикасност крмила хоризонталног репа, константан је број, за конкретну геометрију.
- – отклон крмила хоризонталног репа
- – је коефицијент момента пропињања авиона, усвојено је једноставније, Cm
Градијент линеарне функције Cm = f(Cz) се може одредити из једначине равнотеже авиона, што значи, градијент у пресечној тачки дотичне функције с апсцисом.

Где су:
- – градијент узгона хоризонталног репа
- – градијент узгона крила
Положај тежишта, у којој је статичка уздужна стабилност неутрална, назива се неутрална тачка. Неутрална тачка се обележава с N0. По својој дефиницији, фактички представља аеродинамички центар укупног авиона. Заменом приказаних, веза добија се погодан израз за градијент момента пропињања с променом узгона авиона.
Ово релативно растојање између замишљеног положаја тежишта у неутралној тачки (N0), коме одговара неутрална стабилност, и стварног положаја тежишта авиона , назива се резерва стабилности.[44][45]
За статички стабилне авионе је увек тежиште испред неутралне тачке, односно, тада је негативног предзнака. Код ранијих, класичних ловачких и акробатских авиона, резерва стабилности се кретала у домену:
Крмило хоризонталног лета служи за уздужно управљање авионом. Његовим отклањањем се остварује потребан допринос момента, за уравнотежење авиона при лету на изабраном узгону, односно с изабраном брзином.
или у другом облику

Ефикасност крмила , за остварење момента пропињања, потребног за уравнотежење авиона на режиму лета с жељеном брзином, може се одредити аналитички и експериментално у аеротунелу. Мерењем, у аеротунелу, функције коефицијента момента пропињања од коефицијента узгона, за вариране отклоне крмила, добија се фамилија линија (функција), као на приказаној илустрацији. Пресечна тачка сваке линије Cm = f(Cz) с ординатом, представља Cm, који одговара заданом отклону δh. То су довољни подаци за одређивање , као константе за задату геометрију. На исти начин се одређује и коефицијенат тримовања , с тим што се при томе очитавају пресечне тачке са апсцисом.
При развоју авиона је посебно важно одредити потребне отклоне у полетању, слетању и у екстремном маневру.

Хоризонтални реп, при уравнотежењу авиона, смањује укупни узгон и повећава отпор, што се неповољно одражава на перформансе. Та неповољност, посебно долази до изражаја при надзвучном лету. При надзвучном струјању се неутрална тачка N0 драстично помера уназад, чак за 0,2 la, за толико се повећава и резерва стабилности. Последица тога је и одговарајући равнотежни отклон крмила висине, што значи и прираст отпора. Савременим прилазима пројектовања се то превазилази с увођењем неутралне и негативне статичке уздужне стабилности. Стабилност се обезбеђује уређајима за стабилизацију. Конфигурација с стабилизујућом површином испред крила (систем canard), као на Новом авиону, је повољнија. Принципијелан утицај уравнотежавајућег узгона хоризонталног репа и canard-а, на укупни узгон авиона, приказан је на слици.[42][46]
Динамичка стабилност[уреди | уреди извор]

Динамичка стабилност изучава равнотежу свих сила и момената, независних и зависних од времена, после поремећаја тренутног положаја авиона. Динамички је стабилан авион ако се довољно брзо, после поремећаја, врати и смири у свој првобитни положај. Брзина тог прелазног процеса је дефинисана ваздухопловним нормама, према категоријама авиона. Раније, класичне конфигурације борбених авиона, нису биле проблематичне за испуњење потребних услова и прописа стабилности и управљивости. Савременији авиони, при лету с крозвучним и надзвучним брзинама значајно мењају своје аеродинамичке карактеристике, за рачун постизања већих брзина и ношења већег променљивог терета су потпуно изменили конфигурацију, с неповољним утицајем на стабилност и управљивост. Посебно је неповољан утицај стишљивости ваздуха, на већим брзинама, на стабилност авиона. Развојем паралелних научних грана аутоматског управљања, електронике, рачунарске технологије и техника мерења захтеви се могу, у потпуности, испунити за све конфигурације. Неповољни утицај повећања брзина и нових концепција авиона на аеродинамички и инерциони допринос на динамичку стабилност се умањује пригушивачима, аутопилотима и другим ускладницима, према жељи пројектанта. Увођењем електричних команди лета (FLY-BY-WIRE), створени су услови за неограничене могућности обликовања одговора авиона на поремећај.
Полазна основа за динамичку стабилност је услов равнотеже за свих шест степени слободе кретања авиона. Под претпоставком врло малих померања, односно малих поремећаја у односу на равнотежни услов лета, угаоне брзине p (око x осе), q (око y осе) и r (око z осе) услед поремећаја су мале, те се њихови међусобни производи могу занемарити.[47]
Леве стране једначина су спољне силе и спољни моменти а десне су силе инерције и моменти услед инерције.
Покретни координатни систем се може везати за авион на два начина. Један је када су његове осе уједно и осе тела, тако што се x поклапа са уздужном осом трупа. Други је када се x оса поклапа са вектором брзине . У њему се осе x и z незнатно закрећу у односу на авион, у току његовог лета, с променом нападног угла. Координатни систем лета је практичан, пошто је у њему и компонента брзине w = 0, где је γ = θ - α, што је видљиво из илустрације на слици. У координатном систему лета се претходне једначине равнотеже упрошћавају:
У домену линеарне теорије, односно малих поремећаја, нема последичног прираста спољних сила и момента у равни симетрије, од поремећаја с малом уздужном ротацијом (ваљањем) и бочном транслацијом авиона, као и обрнуто. На основу тога се кретање авиона, са шест степени слободе, може делити на два одвојена облика.[47][48] Уздужно у правцу x и z, с ротацијом око y осе и попречно-смерно у правцу y, с ротацијом око x и z оса.
Уздужно кретање, с држаном палицом (крмило хор. репа се помера са сервопокретачем неповратног дејства), одређују једначине:
| Претходни систем диференцијалних једначина садржи три променљиве: |
Прираштај сила и момената, после поремећаја, може се математички дефинисати развојем Тејлоровог реда, с наведеним променљивим величинама. При томе се, у условима малих поремећаја, чланови вишег реда занемарују, а парцијални изводи првог реда се сматрају да су линеарни.[47]
| Уздужни лет дефинишу једначине: |
|
Бездимензионисањем и математичким трансформацијама долази се до карактеристичне једначине четвртог степена.[47]
Где су:
- – полупречник инерције авиона, око „y“ осе
- – параметар за бездимензионисање времена
- – бездимензиони параметар
- – бездимензионо време
- – комплексна или реална констана, за променљиве, у релацији
- су константе, почетне вредности, променљивих у тренутку поремећаја
Ово су независни чланови карактеристичне једначине. Они дефинишу динамику авиона.
су изводи аеродинамичких карактеристика, по променљивима и по брзинама променљивих, у уздужном кретању. Називају се деривативи стабилности, константни су под истим условима као и основни аеродинамички коефицијенти.[47]
Решење карактеристичне једначине се, за авионе, најчешће своди на два комплексна пара. Један дугопериодични а други краткопериодични. Дугопериодично кретање се назива фугоидно. Њега пилот лако коригује, те није никада проблематично. Краткопериодично је проблематично ако нема довољно пригушење. Поред тога што оптерећује пилота и структуру, смањује и борбене могућности авиона. Посебно је непријатно при лету авиона, с таквим карактеристикама одговора, кроз „узбуркану атмосферу“. Мешање пилота може бити ризично, пошто може, својим кашњењем с реакцијом, ненамерно продубљавати осцилације и довести авион у критичну опасност.[49][50]
Попречно-смерно кретање, с држаном палицом и педалама (крмило правца и крилца се померају са сервопокретачима неповратног дејства), одређују преостале три једначине:

Развојем претходних једначина с променљивим β, Ψ и Φ, добија се слична карактеристична једначина четвртог степена. Њено решење је слично као за уздужно кретање. Бочне осцилације, кратког периода, могу у неким случајевима бити неповољне због слабог пригушења. Ове спрегнуте осцилације, кратког периода, називају се „Холандско ваљање“ – „Дач–рол“ (енгл. Dutch roll).
То је кратко периодично спрегнуто (купловано) осциловање око Z и X оса, као на слици десно.
Одговор авиона зависи, поред његових динамичких карактеристика, од врсте и облика поремећаја. При усклађењу одговора авиона, у процесу оптимизације, се методама анализе и синтезе узимају у обзир сви утицајни фактори. У затворено коло динамике се укључују карактеристике пилота (човека), команди лета (са свим ускладницима), сервопокретача и авиона. Динамика затвореног кола укупног система се детаљно анализира на све типичне облике поремећаја и усклађује се, све док се не добију жељени одговори у оквиру норми и прописа.[49][51]
 |
 |
.
Напомене[уреди | уреди извор]
- ^ Џон Андерсон
„ То је невероватно да и данас, после 100 година након првог лета браће Рајт, групе инжењера, научника, пилота и осталих ваздухопловних стручњака још увек жучно расправљају о томе како авион са крилом генерише узгон? Пуно има различитих објашњења, и ако се сва заснивају на једноставним принципима.[1] ”
Види још[уреди | уреди извор]
Референце[уреди | уреди извор]
- ^ а б "The actual velocity over the top of an airfoil is much faster than that predicted by the "Longer Path" theory and particles moving over the top arrive at the trailing edge before particles moving under the airfoil."Center, Glenn Research (15. 3. 2006). „Incorrect Lift Theory”. NASA. Приступљено 12. 8. 2010.
- ^ Anderson 1997.
- ^ Newton, I. (1726). Philosophiae Naturalis Principia Mathematica, Book II.
- ^ а б в „Welcome to the Beginner's Guide to Aerodynamics Image of jet airplane” (на језику: (језик: енглески)). grc.nasa. Архивирано из оригинала 15. 07. 2012. г. Приступљено 14. 6. 2014. „Welcome to the Beginner's Guide to Aerodynamics Image of jet airplane”
- ^ Драговић 1992, стр. 21.
- ^ „Continuity Equation” (на језику: (језик: енглески)). princeton. Приступљено 14. 6. 2014. „Continuity Equation”
- ^ а б Рендулић 1960, стр. 28–30.
- ^ а б „MECANIQUE DES FLUIDES” (на језику: (језик: француски)). Архивирано из оригинала 26. 01. 2014. г. Приступљено 22. 4. 2018. „MECANIQUE DES FLUIDES”
- ^ а б в „Bernoulli's equation” (на језику: (језик: енглески)). grc.nasa. Архивирано из оригинала 31. 05. 2014. г. Приступљено 14. 6. 2014. „Bernoulli's equation”
- ^ а б Rendulić 1960, стр. 14–15.
- ^ „Mach Number” (на језику: (језик: енглески)). desktop.aero. Архивирано из оригинала 14. 12. 2011. г. Приступљено 14. 6. 2014. „Mach Number”
- ^ а б в „Mach Number – nasa” (на језику: (језик: енглески)). grc.nasa. Архивирано из оригинала 10. 04. 2006. г. Приступљено 14. 6. 2014. „Mach Number – nasa”
- ^ Rendulić 1960, стр. 35–131.
- ^ „Transonic Aerodynamics” (PDF) (на језику: (језик: енглески)). dept.aoe.vt.edu. Архивирано из оригинала (PDF) 20. 10. 2016. г. Приступљено 14. 6. 2014. „Transonic Aerodynamics”
- ^ „Hypersonic Aerodynamics Index” (на језику: (језик: енглески)). grc.nasa. Архивирано из оригинала 25. 09. 2014. г. Приступљено 14. 6. 2014. „Hypersonic Aerodynamics Index”
- ^ Mason, W. H. „Some Hypersonic Aerodynamics” (PDF) (на језику: (језик: енглески)). dept.aoe.vt.edu. Приступљено 14. 6. 2014. „Some Hypersonic Aerodynamics”
- ^ „Free Molecule Aerodynamics” (PDF) (на језику: (језик: енглески)). Архивирано из оригинала 14. 07. 2014. г. Приступљено 22. 4. 2018. „Free Molecule Aerodynamics”
- ^ Shang, J. S. (јануар 2001). „Recent research in magneto-aerodynamics”. Progress in Aerospace Sciences (на језику: (језик: енглески)). 37 (1): 1—20. Bibcode:2001PrAeS..37....1S. doi:10.1016/S0376-0421(00)00015-4. Приступљено 15. 6. 2014. „Recent research in magneto-aerodynamics”
- ^ „Non-Newtonian fluid” (на језику: (језик: енглески)). princeton. Архивирано из оригинала 27. 7. 2014. г. Приступљено 15. 6. 2014. „Non-Newtonian fluid”
- ^ а б „Dimensionless Groups” (на језику: (језик: енглески)). desktop.aero. Архивирано из оригинала 13. 12. 2012. г. Приступљено 15. 6. 2014. „Dimensionless Groups”
- ^ „Dimensionless Forces” (на језику: (језик: енглески)). desktop.aero. Архивирано из оригинала 14. 12. 2011. г. Приступљено 30. 11. 2013. „Dimensionless Forces”
- ^ Дефиниција Рејнолдсовог броја
- ^ „АЕРОДИНАМИЧКА ЛАБОРАТОРИЈА” (на језику: [непоуздан извор?]). vti.mod.gov. Приступљено 15. 6. 2014. „АЕРОДИНАМИЧКА ЛАБОРАТОРИЈА”
- ^ „Flow Regimes” (на језику: (језик: енглески)). physics.info. Приступљено 15. 6. 2014. „Flow Regimes”
- ^ Sane, Sanjay P. (12. 8. 2003). „The aerodynamics of insect flight” (PDF). The Journal of Experimental Biology (на језику: (језик: енглески)). jeb.biologists. 206 (Pt 23): 4191—4308. PMID 14581590. S2CID 17453426. doi:10.1242/jeb.00663. Приступљено 15. 6. 2014. „The aerodynamics of insect flight”
- ^ „Research Group: Aerodynamics and Flight Mechanics” (на језику: (језик: енглески)). southampton. Приступљено 15. 6. 2014. „Research Group: Aerodynamics and Flight Mechanics”
- ^ а б в „Theory of Flight” (на језику: (језик: енглески)). mit. Приступљено 15. 6. 2014. „Theory of Flight”
- ^ а б „Aircraft - Four Fundamental Aerodynamic Forces” (на језику: (језик: енглески)). science.jrank. Приступљено 15. 6. 2014. „Aircraft - Four Fundamental Aerodynamic Forces”
- ^ „What lift” (на језику: (језик: енглески)). grc.nasa. Архивирано из оригинала 09. 03. 2009. г. Приступљено 15. 6. 2014. „What lift”
- ^ „Dimensionless Forces” (на језику: (језик: енглески)). desktop.aero. Архивирано из оригинала 14. 12. 2011. г. Приступљено 15. 6. 2014. „Dimensionless Forces”
- ^ „Wings at High Angles of Attack” (на језику: (језик: енглески)). desktop. Архивирано из оригинала 11. 10. 2012. г. Приступљено 17. 6. 2014. „Wings at High Angles of Attack”
- ^ а б Rendulić 1960, стр. 248–253
- ^ „Desktop Aeronautics = Desktop Aeronautics =” (на језику: (језик: енглески)). desktopaero. Приступљено 17. 6. 2014.
- ^ „Aerodynamics” (на језику: (језик: енглески)). desktop.aero. јануар 2007. Архивирано из оригинала 8. 1. 2014. г. Приступљено 17. 6. 2014. „Aerodynamics:”
- ^ „Aerodynamic Characteristics” (на језику: (језик: енглески)). lissys.demon. Приступљено 17. 6. 2014. „Aerodynamic Characteristics”
- ^ „Tailspin: The Pilots' Terror” (на језику: (језик: енглески)). history.nasa. Приступљено 24. 6. 2014. „Tailspin: The Pilots' Terror”
- ^ Rendulić 1987, стр. 87.
- ^ Rendulić 1987, стр. 527–561.
- ^ „how aeroplane change their direction?” (на језику: (језик: енглески)). answersforpilots. Архивирано из оригинала 30. 09. 2011. г. Приступљено 17. 6. 2014. „how aeroplane change their direction?”
- ^ Bernard Etkin; Lloyd Duff Reid (новембар 1995). „Stability and Control” (на језику: (језик: енглески)). eu.wiley. Приступљено 17. 6. 2014. „Stability and Control”
- ^ а б „STATIC LONGITUDINAL STABILITY” (на језику: (језик: енглески)). iitk.ac.in. Архивирано из оригинала 17. 07. 2015. г. Приступљено 17. 6. 2014. „STATIC LONGITUDINAL STABILITY”
- ^ а б Rendulić 1987, стр. 285–359.
- ^ „Longitudinal Static Stability” (PDF) (на језику: (језик: енглески)). flightlab. 2009. Приступљено 17. 6. 2014. „Longitudinal Static Stability”
- ^ Perkins, C.D., Some Theoretical Developments in Aeroplane Static Longitudinal Stability and Contro AAF TR 5167, 1944.
- ^ Механика лета, 1987. године др Златко Рендулић
- ^ „Canard Aircraft” (на језику: (језик: енглески)). desktop.aero. Архивирано из оригинала 11. 5. 2013. г. Приступљено 17. 6. 2014. „Canard Aircraft”
- ^ а б в г д Ненадовић 1972, стр. 274.
- ^ Perkins, C.D., Hage, r.E. Aeroplane Performance Stability and Control, John Wiley, New York, 1950.
- ^ а б в „Dynamic Stability” (на језику: (језик: енглески)). adg.stanford. Архивирано из оригинала 23. 11. 2014. г. Приступљено 17. 6. 2014. „Dynamic Stability”
- ^ „Longitudinal Dynamic Stability” (PDF) (на језику: (језик: енглески)). flightlab. Приступљено 17. 6. 2014. „Longitudinal Dynamic Stability”
- ^ Ненадовић 1972, стр. 562.
Литература[уреди | уреди извор]
- Anderson, John David (1997). A History of Aerodynamics and its Impact on Flying Machines. New York, NY: Cambridge University Press. ISBN 978-0-521-45435-3.
- Newton, I. (1726). Philosophiae Naturalis Principia Mathematica, Book II. Beograd.
- Rendulić, Zlatko (1960). Aerodinamika. Beograd.
- Rendulić, Zlatko (1987). Механика лета. Beograd.
- Драговић, Томислав (1992). Аеродинамика. Beograd.
- Милошевић, Владимир (2008). Теорија летења. Beograd.
- Ненадовић, Мирослав (1972). Стабилност и управљивост, други део. Beograd.
- Transonic Aerodinamiks, Nord Holland 1986.g., J. Cool
- Аеродинамика, Москва 1980. године, Н. Краснов
- Примењена Аеродинамика, Техничка књига, Беогад 1948. године, Проф. др. Светополк Пивко, дипл. инж.
- Perkins, Courtland Davis; Hage, Robert E. (1950). Aeroplane Performance Stability and Control. New York: John Wiley.
- Perkins, C.D., Some Theoretical Developments in Aeroplane Static Longitudinal Stability and Control AAF TR 5167, 1944.
- Perkins, C.D., Walkowicz, T.F. Stability and Control Flight Test Methods, AAF TR 5242, 1942.
- Burns, B.R.A., Fly-by-wire and Control configured Vehicles-reward and risks, The Aeronatical Journal No 775, febr. 1975.
Спољашње везе[уреди | уреди извор]
- „Welcome to the Beginner's Guide to Aerodynamics”. Архивирано на сајту Wayback Machine (15. јул 2012)



































































































































