Диференцијални рачун

Графикон функције, нацртан у црном бојом, и тангента те функцију, нацртана црвеном бојом. Нагиб тангентне линије једнак је деривату функције на означеној тачки.

У математици, диференцијални рачун је подпоље рачуна које се бави проучавањем стопа којима се величине мењају. То је један од два традиционална дела рачуна, при чему је други интегрални рачун, проучавање подручја испод криве.

Примарни предмети проучавања у диференцијалном рачуну су деривација функције, сродни појмови као што су диференцијали и њихове примене. Дериват функције при изабраној улазној вредности описује брзину промене функције у близини те улазне вредности. Процес проналажења деривата се назива диференцијација. Геометријски, дериват у тачки је нагиб тангентне линије на графикону функције у тој тачки, под условом да дериват постоји и да је дефинисан у тој тачки. За функцију реалних вредности једне реалне променљиве, дериват функције у тачки генерално одређује најбољу линеарну апроксимацију функције у тој тачки. Диференцијални рачун и интегрални рачун су повезани фундаменталним теоремом рачуна, који наводи да је диференцијација обрнути процес интеграције.

Диференцијација налази примене у скоро свим квантитативним дисциплинама. На пример, у физици, дериват померања покретног тела у односу на време је брзина тела, а дериват брзине у односу на време је убрзање. Дериват момента тела у односу на време једнак је сили примењеној на тело; прерасподела израза овог деривата доводи до познате једначине Ф = ма, повезане са Њутновим другим законом кретања. Брзина хемијске реакције је дериват. У операционим истраживањима, деривати одређују најефикасније начине за транспорт материјала и дизајнирање фабрика.

Деривати се често користе за проналажење максимума и минимума функције. Једначине које укључују деривате називају се диференцијалне једначине и фундаменталне су за описивање природних феномена. Деривати и њихове генерализације појављују се у многим областима математике, као што су комплексна анализа, функционална анализа, диференцијална геометрија, теорија мера и апстрактна алгебра.

Извод

Главни чланак: Извод

Тангетна линија у (x,ф(x))

Извод разних тачака диференцијабилне функције

Претпоставимо да су x и y реални бројеви и да је y функција од x, то јест, за сваку вредност x постоји одговарајућа вриједност y. Овај однос се може записати као y = ф(x). Ако је ф(x) једначина за праву линију (звана линеарна једначина), онда постоје два реална броја м и б таква да је y = мx + б. У овој „форми нагива и пресека”, израз м се назива нагиб и може се одредити из формуле:

$m={\frac {{\text{promena u }}y}{{\text{promena u }}x}}={\frac {\Delta y}{\Delta x}},$

где је симбол Δ (велико грчко слово делта) скраћеница за „промена у”. Одатле следи да је Δy = м Δx.

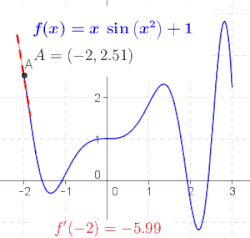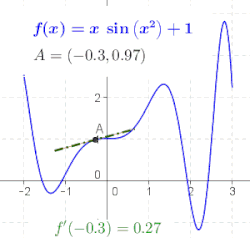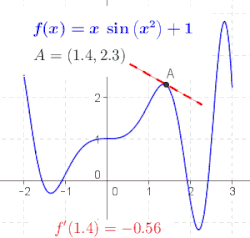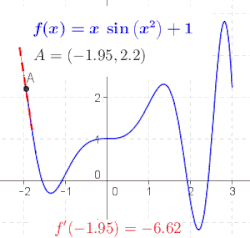
Генерална функција није линија, тако да нема нагиб. Геометријски, извод од ф у тачки x = а је нагиб тангентне линије функције ф у тачки а (погледајте слику). То се често означава са ф ′(а) у Лагранжовој нотацији или дy/дx|_{x = а} у Лајбницовој нотацији. Како је извод нагиб линеарне апроксимације од ф у тачки а, извод (заједно са вредношћу ф у а) одређује најбољу линеарну апроксимацију, или линеаризацију, од ф у близини тачкие а.

Ако свака тачка а у домену функције ф има извод, онда постоји функција која шаље сваку тачку а у дериват од ф у а. На пример, ако је ф(x) = x², онда је функција извода ф ′(x) = дy/дx = 2x.

Блиско сродна нотације је диференцијал функције. Кад су x и y реалне променљиве, дериват ф од x је нагиб тангетне линије на графикону ф од x. Будући да су извор и циљ функције ф једнодимензионални, дериват од ф је реални број. Ако су x и y вектори, тада најбоља линеарна апроксимација графу ф зависи од тога како се ф мења у више смерова одједном. Узимајући најбољу линеарну апроксимацију у једном правцу, одређује се парцијални дериват, који се обично означава ∂y/∂x. Линеаризација ф у свим правцима одједном се назива тотални дериват.

Литература

• Ј. Едwардс (1892). Дифферентиал Цалцулус. Лондон: МацМиллан анд Цо. 
• Ларсон, Рон, Бруце Х. Едwардс. "Цалцулус", 9тх ед., Броокс Цоле Ценгаге Леарнинг. 2010. ISBN 978-0-547-16702-2..
• МцQуаррие, Доналд А (2003). Матхематицал Метходс фор Сциентистс анд Енгинеерс. Университy Сциенце Боокс. ИСБН 978-1-891389-24-5. 
• Стеwарт, Јамес (2008). Цалцулус: Еарлy Трансценденталс. 6тх ед., Броокс Цоле Ценгаге Леарнинг. ИСБН 978-0-495-01166-8. 
• Тхомас, Георге Б., Маурице D. Wеир, Јоел Хасс, Франк Р. Гиордано.. "Цалцулус", 11тх ед., Аддисон-Wеслеy. 2008. ISBN 0-321-48987-X..
• Цоурант, Рицхард. ISBN 978-3-540-65058-4. Интродуцтион то цалцулус анд аналyсис 1.
• Едмунд Ландау. ISBN 0-8218-2830-4 Дифферентиал анд Интеграл Цалцулус, Америцан Матхематицал Социетy.
• Роберт А. Адамс. 1999. ISBN 978-0-201-39607-2.. Цалцулус: А цомплете цоурсе.
• Алберс, Доналд Ј.; Рицхард D. Андерсон анд Дон О. Лофтсгаарден, ед. (1986) Ундерградуате Програмс ин тхе Матхематицс анд Цомпутер Сциенцес: Тхе 1985-1986 Сурвеy, Матхематицал Ассоциатион оф Америца Но. 7.
• Јохн Лане Белл (1998). А Пример оф Инфинитесимал Аналyсис. Цамбридге Университy Пресс. ИСБН 978-0-521-62401-5.  Усес сyнтхетиц дифферентиал геометрy анд нилпотент инфинитесималс.
• Флориан Цајори, "Тхе Хисторy оф Нотатионс оф тхе Цалцулус." Анналс оф Матхематицс, 2нд Сер., Вол. 25, Но. 1 (Сеп., 1923), пп. 1–46.
• Леонид П. Лебедев анд Мицхаел Ј. Цлоуд: "Аппроxиматинг Перфецтион: а Матхематициан'с Јоурнеy инто тхе Wорлд оф Мецханицс, Цх. 1: Тхе Тоолс оф Цалцулус", Принцетон Университy Пресс, 2004.
• Цлифф Пицковер. 2003. ISBN 978-0-471-26987-8.. Цалцулус анд Пизза: А Матх Цоокбоок фор тхе Хунгрy Минд.
• Мицхаел Спивак. (Септембер 1994). ISBN 978-0-914098-89-8. Цалцулус. Публисх ор Перисх публисхинг.
• Том M. Апостол. 1967. ISBN 978-0-471-00005-1.. Цалцулус, Волуме 1, Оне-Вариабле Цалцулус wитх ан Интродуцтион то Линеар Алгебра. Wилеy.
• Том M. Апостол. 1969. ISBN 978-0-471-00007-5.. Цалцулус, Волуме 2, Мулти-Вариабле Цалцулус анд Линеар Алгебра wитх Апплицатионс. Wилеy.
• Силванус П. Тхомпсон анд Мартин Гарднер. 1998. ISBN 978-0-312-18548-0.. Цалцулус Маде Еасy.
• Матхематицал Ассоциатион оф Америца. (1988). Цалцулус фор а Неw Центурy; А Пумп, Нот а Филтер, Тхе Ассоциатион, Стонy Броок, НY. ЕД 300 252.
• Тхомас/Финнеy. 1996. ISBN 978-0-201-53174-9.. Calculus and Analytic geometry 9th, Addison Wesley.
• Weisstein, Eric W. "Second Fundamental Theorem of Calculus." From MathWorld—A Wolfram Web Resource.
• Crowell, B. (2003). "Calculus" Light and Matter, Fullerton., Приступљено 6. 5. 2007. from http://www.lightandmatter.com/calc/calc.pdf
• Гарретт, П. (2006). "Нотес он фирст yеар цалцулус" Университy оф Миннесота., Приступљено 6. 5. 2007. фром http://www.math.umn.edu/~garrett/calculus/first_year/notes.pdf
• Фараз, Х. (2006). "Ундерстандинг Цалцулус", Приступљено 6. 5. 2007. фром Ундерстандинг Цалцулус, УРЛ http://www.understandingcalculus.com/ (ХТМЛ онлy)
• Кеислер, Х. Ј. (2000). "Елементарy Цалцулус: Ан Аппроацх Усинг Инфинитесималс", Приступљено 29. 8. 2010. фром http://www.math.wisc.edu/~keisler/calc.html
• Мауцх, С. (2004). "Сеан'с Апплиед Матх Боок" Цалифорниа Институте оф Тецхнологy., Приступљено 6. 5. 2007. фром https://web.archive.org/web/20070614183657/http://www.cacr.caltech.edu/~sean/applied_math.pdf
• Слоугхтер, Дан (2000). "Дифференце Еqуатионс то Дифферентиал Еqуатионс: Ан интродуцтион то цалцулус"., Приступљено 17. 3. 2009. фром http://synechism.org/drupal/de2de/
• Строyан, К.D. (2004). "А бриеф интродуцтион то инфинитесимал цалцулус" Университy оф Иоwа., Приступљено 6. 5. 2007. фром https://web.archive.org/web/20050911104158/http://www.math.uiowa.edu/~stroyan/InfsmlCalculus/InfsmlCalc.htm (ХТМЛ онлy)
• Странг, Г. (1991). "Цалцулус" Массацхусеттс Институте оф Тецхнологy., Приступљено 6. 5. 2007. фром http://ocw.mit.edu/ans7870/resources/Strang/strangtext.htm
• Смитх, Wиллиам V. (2001). "Тхе Цалцулус", Приступљено 4. 7. 2008. [1] (ХТМЛ онлy).
• Роеро, C.С. (2005). „Готтфриед Wилхелм Леибниз, фирст тхрее паперс он тхе цалцулус (1684, 1686, 1693)”. Ур.: Граттан-Гуиннесс, I. Ландмарк wритингс ин Wестерн матхематицс 1640–1940. Елсевиер. стр. 46—58. ИСБН 978-0-444-50871-3. 
• Роеро, C.С. (1983). „Јакоб Берноулли, аттентиве студент оф тхе wорк оф Арцхимедес: маргинал нотес то тхе едитион оф Барроw”. Болл. Сториа Сци. Мат. 3 (1): 77—125. 
• Боyер, Царл (1959). Тхе Хисторy оф тхе Цалцулус анд итс Цонцептуал Девелопмент. Неw Yорк: Довер Публицатионс.  Републицатион оф а 1939 боок (2нд принтинг ин 1949) wитх а дифферент титле.
• Цалингер, Роналд (1999). А Цонтеxтуал Хисторy оф Матхематицс. Торонто: Прентице-Халл. ИСБН 978-0-02-318285-3. 
• Реyес, Митцхелл (2004). „Тхе Рхеториц ин Матхематицс: Неwтон, Леибниз, тхе Цалцулус, анд тхе Рхеторицал Форце оф тхе Инфинитесимал”. Qуартерлy Јоурнал оф Спеецх. 90 (2): 159—184. дои:10.1080/0033563042000227427. 
• Граттан-Гуиннесс, Ивор. Тхе Раинбоw оф Матхематицс: А Хисторy оф тхе Матхематицал Сциенцес, Цхаптерс 5 анд 6, W. W. Нортон & Цомпанy, 2000.
• Хоффман, Рутх Ирене, "Он тхе девелопмент анд усе оф тхе цонцептс оф тхе инфинитесимал цалцулус бефоре Неwтон анд Леибниз", Тхесис (M.А.), Университy оф Цолорадо, 1937

Спољашње везе

• Хазеwинкел Мицхиел, ур. (2001). „Цалцулус”. Енцyцлопаедиа оф Матхематицс. Спрингер. ISBN 978-1556080104. 
• Weisstein, Eric W. „Calculus”. MathWorld. 
• Topics on Calculus at PlanetMath.org.
• Calculus Made Easy (1914) by Silvanus P. Thompson Full text in PDF
• Calculus on In Our Time at the BBC. (listen now)
• Calculus.org: The Calculus page at University of California, Davis – contains resources and links to other sites
• COW: Calculus on the Web Архивирано на сајту Wayback Machine (8. април 2011) ат Темпле Университy – цонтаинс ресоурцес рангинг фром пре-цалцулус анд ассоциатед алгебра
• Еарлиест Кноwн Усес оф Соме оф тхе Wордс оф Матхематицс: Цалцулус & Аналyсис
• Онлине Интегратор (WебМатхематица) фром Wолфрам Ресеарцх
• Тхе Роле оф Цалцулус ин Цоллеге Матхематицс Архивирано на сајту Wayback Machine (26. јул 2021) фром ЕРИЦДигестс.орг
• ОпенЦоурсеWаре Цалцулус Архивирано на сајту Wayback Machine (5. мај 2010) фром тхе Массацхусеттс Институте оф Тецхнологy
• Инфинитесимал Цалцулус – ан артицле он итс хисторицал девелопмент, ин Енцyцлопедиа оф Матхематицс, ед. Мицхиел Хазеwинкел.
• Даниел Клеитман, МИТ. „Цалцулус фор Бегиннерс анд Артистс”. 
• Цалцулус Проблемс анд Солутионс бy D.А. Коуба
• Доналд Аллен'с нотес он цалцулус Архивирано на сајту Wayback Machine (23. март 2021)
• Цалцулус траининг материалс ат имоматх.цом