Формула пертле
Формула пертле, или алгоритам претле, је математицки алгоритам који се користи за израчунавање површине једноставног многоугла чија темена су одређена уређеним паром у равни.[1] Укрштеним множењем одговарајућих координата добија се поврсина која обухвата многоугао, и одузме је од многоугла који га окрузује да би се одредила површина многоугла унутра. Зове се формула пертле због констаног укрштеног множења за координате које састављају многоугао, као везање пертле.[1] Понекад се зове и метод пертла. Такође, позната је и као Гаусова површинска формула, по Карл Фридрих Гаусу. Користи се у геометрији и шумарству,[2] између осталих области. Такође је позната и као геометрова формула.[3]
Формула се мозе приказати на следећи начин:
где
- А је површина многоугла,
- н је број страница многоугла, анд
- (xи, yи), и = 1, 2,..., н су темена многоугла.
где xн+1 = x1 и x0 = xн, односно yн+1 = y1 и y0 = yн.
Ако су тачке означене супротно од смера казаљки на сату, онда изнад детерминанте су позитивне и абсолутне заграде могу бити изостављене;[3] Ако су тачке означене у смеру казаљки на сату, детерминанте ће бити негативне. Ово је зато што се формула може гледати као посебан случај Гринове теореме.
Примери[уреди | уреди извор]
Морају бити познате тачке у Картезијановој равни. На пример, гледамо троугао са координатама {(2, 1), (4, 5), (7, 8)}. Узмемо прву x-вредност и помнозимо је са другом y-вредношћу, онда узмемо другу x-вредност и помнозимо је са трецом y-вредношћу, и поновимо, и опет поновимо, док не урадимо то за сваку тачку. Ово се може дефинисати формулом:[6]
где xи и yи представљају вредности за респективне координате. Ова формула је само проширање оне која је дата горе за случај н = 3. Коришћењем ње, може се видети да је површина троугла једнака половини апсолутне вредности од 10 + 32 + 7 − 4 − 35 − 16, што је једнако 3. Број варијабла зависи од броја стрница многоугла. На пример, петоугао ће бити дефинисан до x5 анд y5:
Четвороугао ће бити дефинисан до x4 анд y4:
Комплекснији примери[уреди | уреди извор]
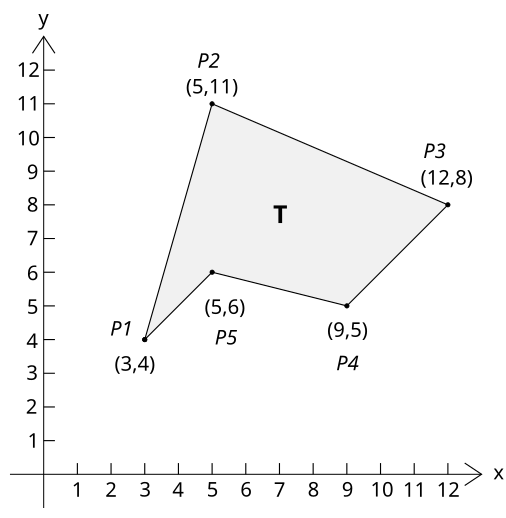
Посматрамо многоугао дефинисан тачкама (3,4), (5,11), (12,8), (9,5), анд (5,6), и илустровам у следећем диаграму:
Површина овог многоугла је:
Објашњење имена[уреди | уреди извор]
Разлог зашто се ова формула зове формула пертле је због честог начина који се користи за њено израчунавање. Овај начин користи матрице. Као пример, гледамо троугао са теменима (2,4), (3,−8), анд (1,2). Онда конструишемо следећу матрицу тако што “ходамо око” троугла и заврћавамо са почетном тачком.[7]
Прво, нацртамо дијагонално доле и ка десно (као што је приказано),
и помножимо два броја повезана дијагоналом, а онда додамо све производе: (2 × −8) + (3 × 2) + (1 × 4) = −6. Урадимо исто са дијагоналама ка доле и лево (приказано доле са претходним дијагоналама):
(4 × 3) + (−8 × 1) + (2 × 2) = 8. Онда, одузмемо ова два броја и узмемо апсолутну вредност разлике: |−6 − 8| = 14. Када поделимо ово са 2 добијемо површину: 7. Овакво организовање бројева чини формулу лакшом за памћење и процењивање. Са свим нацртаним дијагоналама, матрица личи на ципелу са пертлама, што је довело до оваквог имена.
Референце[уреди | уреди извор]
- ^ а б Дахлке, Карл. „Схоелаце Формула”. Приступљено 9. 6. 2008.
- ^ а б Претзсцх, Ханс (2009). Форест Дyнамицс, Гроwтх анд Yиелд: Фром Меасуремент то Модел. Спрингер Сциенце & Бусинесс Медиа. стр. 232—. ИСБН 978-3-540-88307-4.
- ^ а б Браден, Барт (1986). „Тхе Сурвеyор’с Ареа Формула” (ПДФ). Тхе Цоллеге Матхематицс Јоурнал. 17 (4): 326—337. дои:10.2307/2686282. Архивирано из оригинала (ПДФ) 5. 11. 2003. г.
- ^ Схоелаце Тхеорем Архивирано на сајту Wayback Machine (14. мај 2014), Арт оф Проблем Солвинг Wики.
- ^ Wеисстеин, Ериц W. „Полyгон Ареа”. Wолфрам МатхWорлд. Приступљено 24. 7. 2012.
- ^ Рхоад, Рицхард; Георге Милаускас; Роберт Wхиппле (1991). Геометрy фор Ењоyмент анд Цхалленге (неw изд.). МцДоугал Литтелл. стр. 717–718. ISBN 0-86609-965-4.
- ^ IMSA JHMC Guide, Page. 10 "Shoelace" by Cindy Xi






![{\displaystyle {\begin{aligned}\mathbf {A} &={1 \over 2}|3\times 11+5\times 8+12\times 5+9\times 6+5\times 4\\&{}\qquad {}-4\times 5-11\times 12-8\times 9-5\times 5-6\times 3|\\[10pt]&={60 \over 2}=30\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/276683f8e2bba28ac9b98349225ed869479d7813)
