Formula pertle
Formula pertle, ili algoritam pretle, je matematicki algoritam koji se koristi za izračunavanje površine jednostavnog mnogougla čija temena su određena uređenim parom u ravni.[1] Ukrštenim množenjem odgovarajućih koordinata dobija se povrsina koja obuhvata mnogougao, i oduzme je od mnogougla koji ga okruzuje da bi se odredila površina mnogougla unutra. Zove se formula pertle zbog konstanog ukrštenog množenja za koordinate koje sastavljaju mnogougao, kao vezanje pertle.[1] Ponekad se zove i metod pertla. Takođe, poznata je i kao Gausova površinska formula, po Karl Fridrih Gausu. Koristi se u geometriji i šumarstvu,[2] između ostalih oblasti. Takođe je poznata i kao geometrova formula.[3]
Formula se moze prikazati na sledeći način:
gde
- A je površina mnogougla,
- n je broj stranica mnogougla, and
- (xi, yi), i = 1, 2,..., n su temena mnogougla.
gde xn+1 = x1 i x0 = xn, odnosno yn+1 = y1 i y0 = yn.
Ako su tačke označene suprotno od smera kazaljki na satu, onda iznad determinante su pozitivne i absolutne zagrade mogu biti izostavljene;[3] Ako su tačke označene u smeru kazaljki na satu, determinante će biti negativne. Ovo je zato što se formula može gledati kao poseban slučaj Grinove teoreme.
Primeri
[уреди | уреди извор]Moraju biti poznate tačke u Kartezijanovoj ravni. Na primer, gledamo trougao sa koordinatama {(2, 1), (4, 5), (7, 8)}. Uzmemo prvu x-vrednost i pomnozimo je sa drugom y-vrednošću, onda uzmemo drugu x-vrednost i pomnozimo je sa trecom y-vrednošću, i ponovimo, i opet ponovimo, dok ne uradimo to za svaku tačku. Ovo se može definisati formulom:[6]
gde xi i yi predstavljaju vrednosti za respektivne koordinate. Ova formula je samo proširanje one koja je data gore za slučaj n = 3. Korišćenjem nje, može se videti da je površina trougla jednaka polovini apsolutne vrednosti od 10 + 32 + 7 − 4 − 35 − 16, što je jednako 3. Broj varijabla zavisi od broja strnica mnogougla. Na primer, petougao će biti definisan do x5 and y5:
Četvorougao će biti definisan do x4 and y4:
Kompleksniji primeri
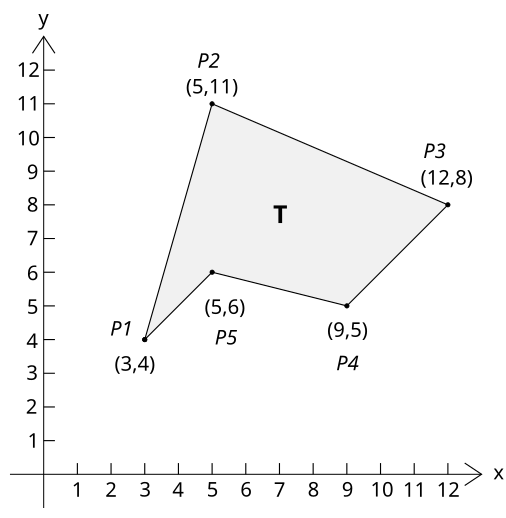
[уреди | уреди извор]Posmatramo mnogougao definisan tačkama (3,4), (5,11), (12,8), (9,5), and (5,6), i ilustrovam u sledećem diagramu:
Površina ovog mnogougla je:
Objašnjenje imena
[уреди | уреди извор]Razlog zašto se ova formula zove formula pertle je zbog čestog načina koji se koristi za njeno izračunavanje. Ovaj način koristi matrice. Kao primer, gledamo trougao sa temenima (2,4), (3,−8), and (1,2). Onda konstruišemo sledeću matricu tako što “hodamo oko” trougla i zavrćavamo sa početnom tačkom.[7]
Prvo, nacrtamo dijagonalno dole i ka desno (kao što je prikazano),
i pomnožimo dva broja povezana dijagonalom, a onda dodamo sve proizvode: (2 × −8) + (3 × 2) + (1 × 4) = −6. Uradimo isto sa dijagonalama ka dole i levo (prikazano dole sa prethodnim dijagonalama):
(4 × 3) + (−8 × 1) + (2 × 2) = 8. Onda, oduzmemo ova dva broja i uzmemo apsolutnu vrednost razlike: |−6 − 8| = 14. Kada podelimo ovo sa 2 dobijemo površinu: 7. Ovakvo organizovanje brojeva čini formulu lakšom za pamćenje i procenjivanje. Sa svim nacrtanim dijagonalama, matrica liči na cipelu sa pertlama, što je dovelo do ovakvog imena.
Reference
[уреди | уреди извор]- ^ а б Dahlke, Karl. „Shoelace Formula”. Приступљено 9. 6. 2008.
- ^ а б Pretzsch, Hans (2009). Forest Dynamics, Growth and Yield: From Measurement to Model. Springer Science & Business Media. стр. 232—. ISBN 978-3-540-88307-4.
- ^ а б Braden, Bart (1986). „The Surveyor’s Area Formula” (PDF). The College Mathematics Journal. 17 (4): 326—337. doi:10.2307/2686282. Архивирано из оригинала (PDF) 5. 11. 2003. г.
- ^ Shoelace Theorem Архивирано на сајту Wayback Machine (14. мај 2014), Art of Problem Solving Wiki.
- ^ Weisstein, Eric W. „Polygon Area”. Wolfram MathWorld. Приступљено 24. 7. 2012.
- ^ Rhoad, Richard; George Milauskas; Robert Whipple (1991). Geometry for Enjoyment and Challenge (new изд.). McDougal Littell. стр. 717–718. ISBN 0-86609-965-4.
- ^ IMSA JHMC Guide, Page. 10 "Shoelace" by Cindy Xi






![{\displaystyle {\begin{aligned}\mathbf {A} &={1 \over 2}|3\times 11+5\times 8+12\times 5+9\times 6+5\times 4\\&{}\qquad {}-4\times 5-11\times 12-8\times 9-5\times 5-6\times 3|\\[10pt]&={60 \over 2}=30\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/276683f8e2bba28ac9b98349225ed869479d7813)
