Хипербола
- За стилску фигуру, погледајте Хипербола (књижевност)

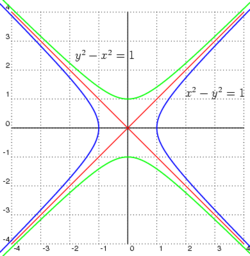
Хипербола (старогрч. ύπερβολή, претеривање) у математици је алгебарска крива другог реда у равни, дата следећом једначином: . Састоји се из два симетрична дела, има два фокуса и две асимптоте дате једначином . Тачка пресека асимптота представља центар симетрије хиперболе. Хипербола, заједно са параболом и елипсом, представља три типа конусних пресека. Конусни пресеци се добијају у пресеку равни са конусном површином (конусна површина се протеже у оба правца).
Хиперболе настају на много начина:
- као крива која представља функцију и у Декартовој равни,[1]
- као стаза коју прати сенка врха сунчаног сата,
- као облик отворене орбите (за разлику од затворене елиптичне орбите), као што је орбита свемирске летелице током замаха планете уз помоћ гравитације или, уопштеније, било које свемирске летелице која премашује брзину бекства најближе планете,
- као путања комете са једном појавом (оне која путује пребрзо да би се икада вратила у Сунчев систем),
- као путања расејања субатомске честице (на коју делују одбојне уместо привлачне силе, али принцип је исти),
- у радио навигацији, када се може одредити разлика између растојања до две тачке, али не и саме удаљености,
и тако даље.
Свака грана хиперболе има два крака који постају равнији (доња кривина) даље од центра хиперболе. Дијагонално супротни кракови, по један из сваке гране, теже у лимиту ка заједничкој линији, која се назива асимптота та два крака. Дакле, постоје две асимптоте, чији је пресек у центру симетрије хиперболе, што се може сматрати тачком огледала око које се свака грана одражава да би формирала другу грану. У случају криве асимптоте су две координатне осе.[1]
Хиперболе деле многа аналитичка својства елипсе као што су ексцентрицитет, фокус и директрису. Обично се кореспонденција може направити само са променом предзнака у неком термину. Многи други математички објекти имају своје порекло у хиперболи, као што су хиперболички параболоиди (површине седла), хиперболоиди („корпе за отпатке“), хиперболична геометрија (прослављена нееуклидска геометрија Лобачевског), хиперболичке функције (sinh, cosh, tanh, итд) , и жировекторски простори (геометрија предложена за употребу у релативистичкој и у квантној механици која није Еуклидска).
Етимологија и историја[уреди | уреди извор]
Реч „хипербола“ потиче од грчке речи ὑπερβολή, што значи „премашено“ или „претерано“, од чега потиче и енглески израз hyperbole. Хиперболе је открио Менехм у својим истраживањима проблема удвостручавања коцке, али су тада назване пресеци тупих конуса.[2] Верује се да је термин хипербола сковао Аполоније из Перге (око 262–190. п. н. е.) у свом делу о конусним пресецима, Коникама.[3] Називи друга два општа конусна пресека, елипса и парабола, потичу од одговарајућих грчких речи за „недостатак“ и „примењен“; сва три назива су позајмљена из раније питагорејске терминологије која се односила на поређење странице правоугаоника фиксне површине са датим сегментом линије. Правоугаоник може да се „примени“ на сегмент (што значи да има једнаку дужину), да буде краћи од сегмента или да премаши сегмент.[4]
Дефиниције[уреди | уреди извор]
Као локус тачака[уреди | уреди извор]


Хипербола се може геометријски дефинисати као скуп тачака (локус тачака) у Еуклидовој равни:
Хипербола је скуп тачака, такав да је за било коју тачку скупа апсолутна разлика растојања на две фиксне тачке (жаришта) константна, обично се означава са [5]
Средња тачка сегмента линије који спаја фокусе назива се центар хиперболе.[6] Линија која пролази кроз жаришта назива се главна оса. Оно садржи врхове , који имају растојање до центра. Удаљеност од фокуса до центра се назива жижна удаљеност или линеарни ексцентрицитет. Количник је ексцентрицитет .
Једначина се може посматрати на другачији начин (погледајте дијаграм):
Ако је круг са средином и полупречником , тада је растојање тачке десне гране до круга једнако растојању до фокуса :
се назива кружна директриса (повезана са фокусом ) хиперболе.[7][8] Да би се добила лева грана хиперболе, мора се користити кружна директриса сродна за . Ово својство не треба мешати са дефиницијом хиперболе уз помоћ директрисе (линије) испод.
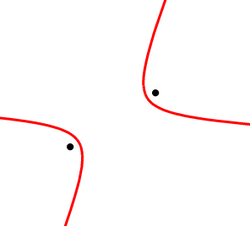
Хипербола са једначином y = A/x[уреди | уреди извор]


црвена: A = 1; магента: A = 4; плава: A = 9
Ако је 'xy-координатни систем ротиран око почетка за угао и нове координате су додељене, тада је .
Правоугаона хипербола (чије су полуосе једнаке) има нову једначину . Решавање за даје
Дакле, у систему xy-координата график функције са једначином
- је правоугаона хипербола у потпуности у првом и трећем квадранту са
- координатне осе као асимптоте,
- права као главна оса,
- центар и полу-оса
- врхови
- полу-конусни пресек и полупречник закривљености на врховима
- линеарни ексцентрицитет и ексцентрицитет
- тангента у тачки
Ротација оригиналне хиперболе за доводи до правоугаоне хиперболе у потпуности у другом и четвртом квадранту, са истим асимптотама, центар, конусни пресек, полупречник закривљености на врховима, линеарни ексцентрицитет и ексцентрицитет као у случају ротације , са једначином
- полуосе
- права као главна оса,
- темена
Померање хиперболе са једначином тако да је нови центар , даје нову једначину
а нове асимптоте су и .
Параметри облика остају непромењени.
Својства директрисе[уреди | уреди извор]

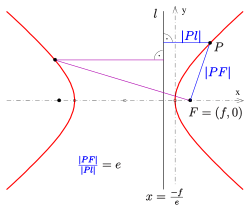
Две праве на удаљености од центра и паралелно са малом осом називају се директрисе хиперболе (погледајте дијаграм).
За произвољну тачку хиперболе количник удаљености до једног фокуса и до одговарајуће директрисе (погледајте дијаграм) је једнак ексцентрицитету:
Доказ за пар следи из чињенице да и задовољавају једначину
Други случај се доказује аналогно.

Инверзна изјава је такође тачна и може се користити за дефинисање хиперболе (на начин сличан дефиницији параболе):
За било коју тачку (фокус), било која права (директриса) није кроз и било који реални број са скуп тачака (локус тачака), за који је количник растојања до тачке и до праве је
- је хипербола.
(Избор даје параболу и ако је елипсу.)
- Доказ
Нека је и претпоставимо да је тачка на кривој. Директриса има једначину . Са , релација производи једначине
- and
Замена даје
Ово је једначина елипсе () или параболе () или хипербола (). Сви ови недегенерисани конуси имају заједничко порекло као врх (види дијаграм).
Ако је , уведите нове параметре тако да је , а онда горња једначина постаје
што је једначина хиперболе са центром , x-осом као главном осом и главном/споредном полуосом .
Једначине хиперболе[уреди | уреди извор]
Параметарска једначине хиперболе је:
У Декартовом координатном систему, хипербола се описује једначином:
Особине[уреди | уреди извор]
Постоје две важне особине фокуса хиперболе :
- За сваку тачку хиперболе Р, важи (d је растојање):
Ово својство омогућава и следећу дефиницију хиперболе: Геометријско место тачака у равни, за које је апсолутна вредност разлике растојања од било које тачке до две фиксне тачке у истој равни (два фокуса), константна. - Тангента на сваку тачку хиперболе Р представља бисектрису .
Дужина лука[уреди | уреди извор]
Дужина лука хиперболе нема елементаран израз. Горња половина хиперболе може се параметризовати као
Тада се интеграл који даје дужину лука од до може израчунати као:
Након употребе замене , ово се такође може представити коришћењем непотпуног елиптичког интеграла друге врсте са параметром :
Користећи само реалне бројеве, ово постаје[9]
где је непотпуни елиптички интеграл прве врсте са параметром и је Гудерманова функција.[10]
Референце[уреди | уреди извор]
- ^ а б Oakley (1944, стр. 17)
- ^ Heath, Sir Thomas Little (1896), „Chapter I. The discovery of conic sections. Menaechmus”, Apollonius of Perga: Treatise on Conic Sections with Introductions Including an Essay on Earlier History on the Subject, Cambridge University Press, стр. xvii—xxx.
- ^ Boyer, Carl B.; Merzbach, Uta C. (2011), A History of Mathematics, Wiley, стр. 73, ISBN 9780470630563, „It was Apollonius (possibly following up a suggestion of Archimedes) who introduced the names "ellipse" and "hyperbola" in connection with these curves.”
- ^ Eves, Howard (1963), A Survey of Geometry (Vol. One), Allyn and Bacon, стр. 30—31
- ^ Protter & Morrey (1970, стр. 308–310)
- ^ Protter & Morrey (1970, стр. 310)
- ^ Apostol, Tom M.; Mnatsakanian, Mamikon A. (2012), New Horizons in Geometry, The Dolciani Mathematical Expositions #47, The Mathematical Association of America, стр. 251, ISBN 978-0-88385-354-2
- ^ The German term for this circle is Leitkreis which can be translated as "Director circle", but that term has a different meaning in the English literature (see Director circle).
- ^ Carlson, B. C. (2010), „Elliptic Integrals”, Ур.: Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
- ^ Gudermann, Christoph (1833). Theorie der Potenzial- oder cyklisch-hyperbolischen Functionen [Theory of Potential- or Circular-Hyperbolic Functions] (на језику: немачки). G. Reimer.
Литература[уреди | уреди извор]
- Kazarinoff, Nicholas D. (2003), Ruler and the Round, Mineola, N.Y.: Dover, ISBN 0-486-42515-0
- Oakley, C. O., Ph.D. (1944), An Outline of the Calculus, New York: Barnes & Noble
- Protter, Murray H.; Morrey, Charles B., Jr. (1970), College Calculus with Analytic Geometry (2nd изд.), Reading: Addison-Wesley, LCCN 76087042
- Woodhouse, N. M. J. (2003), Special Relativity, London: Springer, стр. 71, ISBN 978-1-85233-426-0
- Abramowitz, Milton; Stegun, Irene A., ур. (1972), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover Publications, ISBN 978-0-486-61272-0
- Rickey, V. Frederick; Tuchinsky, Philip M. (1980). „An application of geography to mathematics: History of the integral of the secant” (PDF). Mathematics Magazine. 53 (3): 162—166. doi:10.1080/0025570X.1980.11976846.
- Ringermacher, Harry I.; Mead, Lawrence R. (2009). „A new formula describing the scaffold structure of spiral galaxies”. Monthly Notices of the Royal Astronomical Society. 397 (1): 164—171. doi:10.1111/j.1365-2966.2009.14950.x
 .
. - Robertson, John S. (1997). „Gudermann and the simple pendulum”. The College Mathematics Journal. 28 (4): 271—276. JSTOR 2687148. doi:10.2307/2687148.
- Romakina, Lyudmila N. (2018). „The inverse Gudermannian in the hyperbolic geometry”. Integral Transforms and Special Functions. 29 (5): 384—401. doi:10.1080/10652469.2018.1441296.
- Roy, Ranjan; Olver, Frank W. J. (2010), „4. Elementary Functions”, Ур.: Olver, Frank W. J.; et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
- Sala, Kenneth L. (1989). „Transformations of the Jacobian amplitude function and its calculation via the arithmetic-geometric mean” (PDF). SIAM Journal on Mathematical Analysis. 20 (6): 1514—1528. doi:10.1137/0520100.
Спољашње везе[уреди | уреди извор]
- Информације о хиперболи
- Hazewinkel Michiel, ур. (2001). „Hyperbola”. Encyclopaedia of Mathematics. Springer. ISBN 978-1556080104.
- Apollonius' Derivation of the Hyperbola at Convergence
- Frans van Schooten: Mathematische Oeffeningen, 1659
- Weisstein, Eric W. „Хипербола”. MathWorld.






















































































![{\displaystyle s=ib{\Biggr [}E\left(iv\,{\Biggr |}\,1+{\frac {a^{2}}{b^{2}}}\right){\Biggr ]}_{\operatorname {arcosh} {\frac {x_{2}}{a}}}^{\operatorname {arcosh} {\frac {x_{1}}{a}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f5d0c6796e5b98e06e3a1823868ff218bade95d)
![{\displaystyle s=b\left[F\left(\operatorname {gd} v\,{\Biggr |}-{\frac {a^{2}}{b^{2}}}\right)-E\left(\operatorname {gd} v\,{\Biggr |}-{\frac {a^{2}}{b^{2}}}\right)+{\sqrt {1+{\frac {a^{2}}{b^{2}}}\tanh ^{2}v}}\,\sinh v\right]_{\operatorname {arcosh} {\tfrac {x_{1}}{a}}}^{\operatorname {arcosh} {\tfrac {x_{2}}{a}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11d1ab93c8a700748cb97ea55602b710787b1250)
