Нормални мод

Различити нормални модови у 1Д-решетки.

Нормални мод једног осцилујућег система је начин кретања у коме се сви делови система крећу синусоидно на истој фреквенцији. Фреквенције нормалних модова система су познате као природне или резонантне фреквенције. Један физички објекат, као што је зграда, мост или молекул, поседује скуп нормалних модова (и кореспондирајућих фреквенција) које су зависне од његове структуре и састава.

Нормални модови механичких система су једно-фреквентна решења једначина кретања. Најгенералније кретање система је суперпозиција његових нормалних модова. Модови су названи нормални зато што они могу да се крећу независно. Екситација једног мода неће никад проузроковати кретање другог мода. У многим системима то је еквивалентно редуковању колекције здружених осцилација у скуп раздвојених ефективних осцилатора.

Уобичајено је да се користи систем састављен од тела и опруге у илустровању еластичних структура. Када је такав систем побуђен на једној од његових природних фреквенција, све масе у његовом саставу се крећу на истој фреквенцији. Фазе тих маса су исте, тако да оне све пролазе кроз еквилибријум и максималну аплитуду истовремено. Практични значај тога се може илустровати моделом зграде. Ако земљотрес побуди систем близо једне од природних фреквенција, померање једног спрата у односу на други - у зависности оф мода - може бити максималан. Очевидно, зграде могу да поднесу оваква померања до одређене тачке. Моделовање зграда путем налажења њихових нормалних модова је један лак начин да се провери безбедност грађевинског дизајна. Концепт нормалиних модова исто тако налази примену у таласној теорији, оптици, квантној механици, и молекуларној динамици.

Пулсирање у нормалном моду

Спрегнути осцилатори

Посматрајмо два еквивалентана тела (која нису под утицајем гравитације), једнаких маса M, која су повезана са три опруге, свака од којих има константу опруге К. Тела су повезана на следећи начин:

где су крајње тачке фиксиране и не могу се померити. Ми ћемо користити x₁(т) да означимо хоризонтано померање леве масе, и x₂(т) да означимо померање десне масе. Ако обележимо други извод од x(т) у односу на време са ${\ddot {x}}$, једначине кретања су:

$M{\ddot {x}}_{1}=-Kx_{1}+K(x_{2}-x_{1})\,\!$

$M{\ddot {x}}_{2}=-Kx_{2}+K(x_{1}-x_{2})\,\!$

Пошто очекујемо осцилаторно кретање, можемо користити:

$x_{1}(t)=A_{1}e^{i\omega t}\,\!$

$x_{2}(t)=A_{2}e^{i\omega t}\,\!$

Замена ових израза у једначине кретања даје:

$-\omega ^{2}MA_{1}e^{i\omega t}=-2KA_{1}e^{i\omega t}+KA_{2}e^{i\omega t}\,\!$

$-\omega ^{2}MA_{2}e^{i\omega t}=KA_{1}e^{i\omega t}-2KA_{2}e^{i\omega t}\,\!$

Еxпонцијални фактор је заједнички у свим сабирцима, тако да се једначине могу поједноставити:

$(\omega ^{2}M-2K)A_{1}+KA_{2}=0\,\!$

$KA_{1}+(\omega ^{2}M-2K)A_{2}=0\,\!$

Или у матричној репресентацији:

${\begin{bmatrix}\omega ^{2}M-2K&K\\K&\omega ^{2}M-2K\end{bmatrix}}{\begin{pmatrix}A_{1}\\A_{2}\end{pmatrix}}=0$

Да би ова једначина имала нетривијална решења, лева матрица мора бити сингуларна, тако да је детерминанта те матрице једнака нули:

$(\omega ^{2}M-2K)^{2}-K^{2}=0\,\!$

Решавајући по $\omega$, добијају се два решења:

$\omega _{1}={\sqrt {\frac {K}{M}}},$

$\omega _{2}={\sqrt {\frac {3K}{M}}}.$

Ако заменимо ω₁ у матрицу и решимо за (А₁, А₂), добијамо (1, 1). Ако заменимо ω₂, добијамо (1, −1). (Ови вектори су својствени вектори, и фреквенције су својствене вредности.)

Први нормални мод је:

${\begin{pmatrix}x_{1}(t)\\x_{2}(t)\end{pmatrix}}=c_{1}{\begin{pmatrix}1\\1\end{pmatrix}}\cos {(\omega _{1}t+\phi _{1})}$

То одговара ситуацији где се обе масе крећу у истом смеру. Због тога, фреквенција је иста као да су масе повезане чврстом цеви.

Други нормални мод је:

${\begin{pmatrix}x_{1}(t)\\x_{2}(t)\end{pmatrix}}=c_{2}{\begin{pmatrix}1\\-1\end{pmatrix}}\cos {(\omega _{2}t+\phi _{2})}$

То је слућај где се масе крећу у супротним смеровима, док је центар масе стационаран. Генерално решење је суперпозиција нормалних модова где су ц₁, ц₂, φ₁, и φ₂, одређени почетним условима проблема.

Демонстрирани процес се може генералисати користећи формализам Лагранжеве механике или Хамилтонове механике.

Стационарни таласи

Стационарни талас је континуална форма нормалног мода. У стојећем таласу, сви просторни елементи (и.е. (x, y, з) координате) осцилују на истој фреквенцији и фази (достижући еквилибријску тачку заједно), али имају различите амплитуде.

Општи облик стојећег таласа је:

$\Psi (t)=f(x,y,z)(A\cos(\omega t)+B\sin(\omega t))$

где ƒ(x, y, з) представља зависност амплитуде од локације, и цос\син су осцилације у функцији времена.

Физички, стојећи таласи се формирају интерференцијом (суперпозицијом) таласа и њихових рефлекција (мада се може казати и супротно; да је кретање таласа суперпозиција стационарних таласа). Геометријски облик средине одређује облик интерференције, и стога одређује ƒ(x, y, з) форму стојећег таласа. Ова просторна зависност се назива нормални мод.

Обично, проблеми са континуираном зависношћу од (x, y, з) немају коначан број нормалних модова, него имају бесконачно много нормалних модова. Ако је проблем ограничен (тј. ако је дефинисан на коначном просторном сегменту) онда постоји пребројиво много (дискретно бесконачно) нормалних модова (који су обично нумерисани са н = 1, 2, 3, ...). Ако проблем није ограничен, постоји континуалан спектар нормалних модова.

Дозвољене фреквенције су зависне од нормалних модова, као и од физичких константи проблема (густина, напон, притисак, итд. ) који одређују фазну брзину таласа. Скуп свих могућих нормалних фреквенција се зове фреквенциски спектар. Обично је свака фреквенција модулисана амплитудом на којој је настала, што ствара графикон [спектралне снаге] осцилација.

У музичком смислу, нормални модови вибрационог инструмента (гудачке жице, ваздушна цев, бубњеви, етц.) се зову "хармоници" или "виши хармоници".

Еластична чврста тела

Види: Ајнштајново чврсто тело и Дебајев модел

У сваком чврстом телу на било којој температури, примарне честице (тј. атоми или молекуле) нису стационарни, него вибрирају око средишних позиција. Карактеристика изолационих материјала да не спроводе топлотну енергију је скоро искључиво заснован на овим вибрацијама. Многе физичке особине чврстих тела (као што је еластични модул) могу се предвидети ако су познате фреквенције на којима честице осцилују. Најједноставнија претпоставка (по Ајнштајну) је да све честице осцилују око својих средњих позиција на накој природној фреквенцији ν. То је еквивалентно претпоставци да сви атоми вибрирају независно на фреквенцији ν. Ајнштајн је исто тако претпоставио да су дозвољена енергетска стања тих осцилација хармоници, или интегрални производ од хν. Спектар таласних форми се може математички описати користећи Фуријеве редове синусоидних густинских флуктуација (или термалних фотона).

Фундаментална фреквенција и првих шест хармоника вибрирајуће нити. Математика таласне пропагације у кристалним чврстим телима се састоји од третирања хармоника као да су идеални Фуријеови редови синусоидних густинских флуктуација (или атомских таласа).

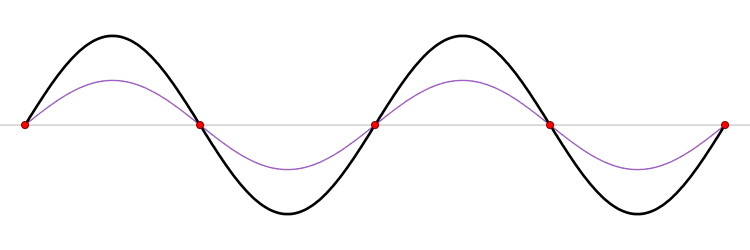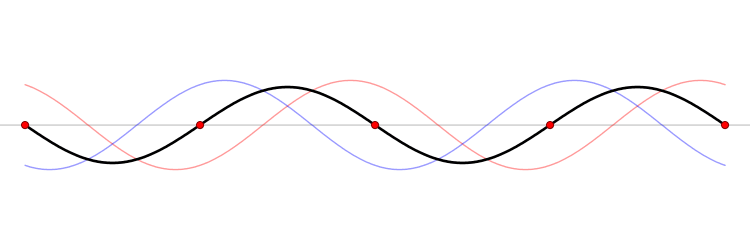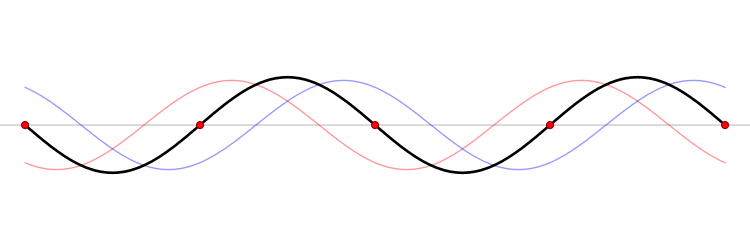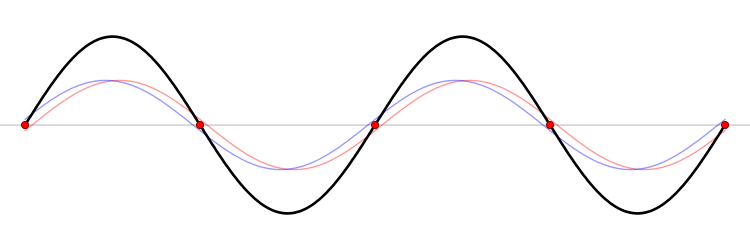
Дебај је касније увидео да је сваки осцилатор стално и интиматно спрегнут са суседним осцилаторима. С тим на уму, и замењујући Ањштајнове идентичне неспрегнуте осцилаторе са истим бројем спрегнутих осцилатора, Дебај је повезао еластичне вибрације једно-димензионалног чврстих тела са бројем специјалних вибрационих модова растегнуте нити (видите слику). Ћист тоне најнижег нивоа или фреквенције се назива фундаментални тон, а умношци те фреквенције се зову виши хармоници. Он је доделио једном осцилаторy фреквенцију фундаменталне вибрације целог чврстог тела. Осталим осцилаторима је доделио хармоничке фреквенције које су релативне у односу на фундаменталну фреквенцију, тако да је највиша фреквенција ограничена кретањем најмање примарне целине.

Нормални модови вибрација кристала су у упшеном смислу суперпозиције многих хармоника, где сваки има одговарајућу амплитуду и фазу. Више таласне дужине (ниже фреквенције) фотона су еквивалентне акустичним вибрацијама. Обе врсте таласа, лонгитудални и транверзални, се могу пропагирати кроз чврста тела, док се у принципу, само лонгитудални таласи преносе у течностима.

У лонгитудалном (или акустичком) моду, померање честица око њихових еквилибриских позиција је коинсидентно са пропагационим правцем таласа. Механички лонгитудални таласи се могу сматрати компресивним таласима. У трансверзалним (или оптичким) модовима, индивидуалне честице се крећу перпендикуларно на правац пропагације таласа.

Са гледишта квантне теорије, средња енергија нормалног вибрационог мода кристала са карактеристичном фреквенцијом υ је:

$E(v)={\frac {1}{2}}hv+{\frac {hv}{e^{hv/kt}-1}}$

Члан (1/2)хυ представља "енергију нулте тачке", или енергију коју ће један осцилатор имати у апсолутној нули. Е (ν ) постаје класична вредност кТ на високим температурама.

$E(v)=kT\left[1+{\frac {1}{12}}{\frac {hv^{2}}{kT}}+O\left({\frac {hv}{kT}}\right)^{4}+\ldots \right]$

Ентропија по нормалном моду је:

${\begin{aligned}S\left(v\right)&=\int _{0}^{T}{\frac {d}{dT}}E\left(v\right){\frac {dT}{T}}\\&={\frac {E\left(v\right)}{T}}-k\log \left(1-e^{-{\frac {hv}{kT}}}\right)\\\end{aligned}}$

Слободна енергија је:

$F(v)=E-TS=kT\log \left(1-e^{-{\frac {hv}{kT}}}\right)$

која, за кТ >> хν, кежи ка:

$F(v)=kT\log \left({\frac {hv}{kT}}\right)$

Да би смо израчунали унутрашњу енергију и специфицичну топлоту, морамо да знамо број нормалних вибрационих модова фреквенције између вредности ν и ν + дν. Ако дозволимо том броју да буде ф (ν)дν, и будући да је тотални број нормалних модова 3Н, функција ф (ν) је дата са:

$\int f(v)dv=3N$

Решавајући интеграл се преко свих фреквенција кристала, добија се унутраншња енергија, У:

$U=\int f(v)E(v)dv$

Квантна механика

У квантној механици, стање $\ |\psi \rangle$ система се описује таласном функцијом $\ \psi (x,t)$ која је решење Шредингерове једначине. Квадрат апсолутне вредности од $\ \psi$ ,и.е.

$\ P(x,t)=|\psi (x,t)|^{2}$

је вероватноћа налажења честице у месту x у времену т. Обично, ова једначина описује неку врсту потенцијала, у ком случају таласна функција се разлаже у суперпозицију енергетских квантних стања, која осцилују са фреквенцијом $\omega =E_{n}/\hbar$. На тај начин се може написати:

$|\psi (t)\rangle =\sum _{n}|n\rangle \left\langle n|\psi (t=0)\right\rangle e^{-iE_{n}t/\hbar }$

Еиген стања имају физичка значења, и нису само ортонормиране базе. Кад се енергија система мери, таласна функција се своди у једно од својих еиген стања, и тако се таласна функција честице описује чистим еиген стањем које одговара мереној енергији.

Види још

• Специфични типови:
  • Лонгитудални мод
  • Трансверзни мод
• Физичке апликације:
  • Таласи
  • Оптика
  • Хармонијски осцилатори
  • Вибрациона спектроскопија
  • Квантна теорија
    • Шредингерова једначина
    • Таласна функција
    • Мерења у квантној механици
  • Хармоничне серије (музика)
  • Сеизмологија
  • Против земљотресни енжињеринг
  • Мод облика
  • Собна акустика
• Математички алати:
  • Линеарна алгебра
  • Еиген вектори
  • Диференцијалне једначине
  • Фуријеова анализа
  • Стурм–Лиоувилле теорија
  • Проблем Граничних Вредноти

Спољашње везе

• Симулација спрегнутих осцилатора.
• Симулација нормалних модова канапа, бубња, анд шипке.
• Фотограпија шоље кафе која вибрира на фреквенцији нормалног мода