Кирхофови закони
Кирхофови закони су две једначине које описују однос струје и напона у електричним колима. Први пут су описане 1845. године од стране Густаф Кирхофа.[1][2] Ове једначине су наставак радова Георга Ома и претходили су радовима Максвела.[3] Имају широку примену у електротехници и називају се Кирхофовим правилима или Кирхофови законима.[4]
Оба Кирхофова закона се могу схватити као облик Максвелових једначина у границама ниских фреквенција — уобичајеног назива 'DC' кола.[5][6] Ови закони служе као прва апроксимација за наизменична кола.[7]
Први Кирхофов закон[уреди | уреди извор]

Назива се још и Кирхофов струјни закон.
У сталном струјном пољу распоред електричних наелектрисања у простору је временски непроменљив. На место покретних наелектрисања која напусте запремину долази иста количина нових покретних наелектрисања. Количина наелектрисања која се улије у чвор мора да буде једнака количини која за исто време отекне из чвора.
Ово је Закон континуитета за наелектрисање:
Ако релацију поделимо временом , добијамо за струју:
- или
Струја је позитивна уколико је усмерена ка чвору или негативна уколико напушта чвор.
- .
Једначина важи и за комплексне вредности струје:
Ограничења[уреди | уреди извор]
Први Кирхофов закон, у свом уобичајеном облику, зависи од претпоставке да струја тече само у проводницима, и да кад год струја тече у један крај проводника, одмах истиче на други крај. Ово није безбедна претпоставка за наизменична кола. Могуће је коришћење облика Првог Кирхофовог закона разматрајући "паразитске капацитивности" које су распоређене дуж проводника.[тражи се извор] Али ово доста одудара од једноставности Првог Кирхофовог закона и чини касније описано тополошко посматрање електричних кола немогућим. Значајни прекршаји Првог Кирхофовог закона могу да настану[тражи се извор] на само 60Hz, што није висока фреквенција.
Другим речима, Први Кирхофов закон је важећи само уколико је укупно наелектрисање, , константно у разматраном опсегу. Када се разматра проблем у коначном опсегу, могуће је мењати густину наелектрисања. Пошто се наелектрисање одржава, ово може само да се деси због протока наелектрисања у коначном опсегу. Овај проток представља струју мреже и Први Кирхофов закон је прекршен.
Формално, из запреминског интеграла једначине континуитета струје,
где је вектор густине струје и је запремина области.
Конвертујући запремински интеграл у површински интеграл коришћењем теореме дивергенције
Одатле,
Десна страна се губи уколико је временски независан. Ако се практично сва налазе у малим областима, нпр. проводне жице, онда се лева страна интерпретира као сума дискретних струја и Први Кирхофов закон важи, под условом да важи .
Посебан случај где Први Кирхофов закон није тачан је струја улази једну плочу кондензатора. Да бисмо илустровали ову тачку, замислите једну затворену површину око те плоче, струја улази кроз површину, али не излази, кршећи Први Кирхофов закон. Свакако, струја кроз затворену површину око целог кондензатор ће задовољавати Први Кирхофов Закон, јер струја која улази у једну плочу кондензатора излази кроз другу, а то је углавном све што је важно у анализи кола. Међутим постоји проблем када се разматра само једна плоча. Други чест пример је струја која улази у антену радио предајника, али не излази из истог (Џонсон и Грејем).
Максвел је представио концепт заменских струја како би објаснио ову ситуацију. Струја која се улива у плочу кондензатора је једнака брзини акумулације наелектрисања, и слично, једнака брзини промене електричног флукса (СИ систем јединица за обе мере, електрични флукс и наелектрисање, су Кулони).[8] Ова брзина промене флукса, , је оно што је Максвел назвао заменским струјама ;
Ако се укључе заменске струје, Први Кирхофов закон се још једном потврђује. Заменске струје нису праве струје, по томе што се не састоје од померајућих наелектрисања; треба их посматрати више као фактор корекције који чини Први Кирхофов закон важећим. У случају кондензаторске плоче, права струја која улази у плочу се тачно поништава са заменском струјом која напушта плочу, и путује ка супротној плочи.
Ово такође може да се изрази преко количина векторских поља преко дивергенције Амперовог закона са Максвеловом корекцијом, и комбинујући Гаусов закон, добија се:
Ово је просто једначина одржавања наелектрисања (у интегралној форми, она говори да је струја која тече од затворене површине једнака брзини губитака наелектрисања унутар ограничене запремине (теорема дивергенције). Кирхофов први закон је еквивалентан тврдњи да је дивергенција струје 0, тачна за временску непроменљиву , или увек тачна ако се укључи заменска струја са .
Коришћење[уреди | уреди извор]
Матрична верзија Првог Кирхофовог закона је основа већине програма за симулацију електричних кола, као што је СПАЈС. Први Кирхофов закон комбинован са Омовим законом се користи у анализи чворова.
Други Кирхофов закон[уреди | уреди извор]
Назива се још и Кирхофов напонски закон.
У свакој струјној контури разгранатог кола алгебарски збир напона на свим отпорима једнак је алгебарском збиру свих електромоторних сила у тој контури. Ово постаје јасније када се сагледа да је поларитет напона на отпорима супротан поларитету извора напона, па збир даје нулу.
Математички изражено ово је:
За комплексне вредности напона важи:
Овај закон се заснива на једном од Максвелових једначина (Максвел - Фарадејев закон индукције) у коме се наводи да је пад напона око једне затворене контуре једнак стопи промене флукса који сече ту контуру. Вредност флукса зависи од захваћене области контуре и јачине магнетног поља. Други Кирхофов закон каже да је вредност напона те контуре једнака нули. Максвелове једначине нам говоре да ће напон контуре бити мали уколико је захваћена област контуре мала, магнетно поље је слабо, и/или магнетно поље се полако мења.
Рутинске инжењерске операције - као што је коришћење коаксијалног кабла и увијених парица - могу да се користи да се смање лутајућа магнетна поља. Коришћењем ових техника се ствара средина, где други Кирхофов закон постаје користан за апроксимације у истим ситуацијама у којима је његова примена била непрецизна пре коришћења ових мера.
Ограничења[уреди | уреди извор]
Други Кирхофов закон се заснива на претпоставци да не постоји променљиво магнетно поље које утиче на затворену контуру . Ово није безбедна претпоставка за наизменична кола. У присуству променљивог магнетног поља, електрично поље није конзервативно векторско поље. Због тога, електрично поље не може бити градијент неког потенцијала. Тј., интеграл електричног поља око контуре није једнак нули, што директно противречи Првом Кирхофовом закону.
Могуће је спасити форму Другог Кирхофовог закона разматрајући паразитске индуктивности (укључујући међусобне индукције) које се налазе дуж проводника. Оне се третирају као замишљени елементи кола који производе пад напона једнак брзини промене флукса. Али, овај поступак доста одскаче од једноставности Другог Кирхофовог закона и онемогућава посматрање кола као тополошке шеме.
Уопштење[уреди | уреди извор]
У једносмерним колима, пад напона око било које контуре је једнак нули. Ово укључује и замишљене контуре које се налазе произвољно у простору -- нису ограничене контурама које сачињавају елементи кола и проводници. При малим фреквенцијама, ово је последица Фарадејевог закона индукције (који је један од Максвелових једначина).
Ово има практичну примену у ситуацијама које користе "статички електрицитет".
Тополошке шеме електричних кола[уреди | уреди извор]
У апроксимације које су довеле до Кирхофових закона спада и идеја да физички и геометријски распоред елемената у колу није битан. Топологија је једина битна ставка и одређена је распоредом проводника и елемената кола који су повезани на чворове. Такво коло се може третирати чворовима и гранама у теорији графова. Другим речима, Кирхофови закони кажу да је дозвољено третирати електрична кола само као чисту шему. Ово је веома корисно и моћно поједностављивање.
Овај принцип ради добро у подручју једносмерних струја, али то је само прва апроксимација за наизменична кола. За веће снаге, високе прецизности, и/или високе фреквенције рада, јавља се одступање од Кирхофових закона. Не може се занемарити физички и геометријски распоред кола, јер одређује величину паразитне капацитивности и индуктивности.
Пример[уреди | уреди извор]
Претпоставимо постојање електричне мреже која се састоји од два извора напона и три отпорника:
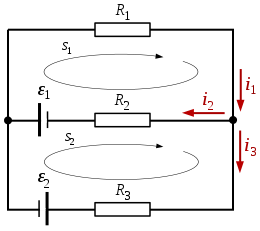
Према првом Кирхофовом закону имамо
Други Кирхофов закон се примењује на затвореној контури s1 и даје
Други Кирхофов закон се примењује на затвореној контури s2 и даје
Тако добијамо линеаран систем једначина :
Под претпоставком
решење је
има негативан знак, што значи да је смер супротан претпостављеном правцу (правац дефинисан на слици ).
Види још[уреди | уреди извор]
Референце[уреди | уреди извор]
- ^ Oldham, Kalil T. Swain (2008). The doctrine of description: Gustav Kirchhoff, classical physics, and the "purpose of all science" in 19th-century Germany (Ph. D.). University of California, Berkeley. стр. 52. Docket 3331743.
- ^ Oldham, Kalil T. Swain (2008). The doctrine of description: Gustav Kirchhoff, classical physics, and the "purpose of all science" in 19th-century Germany (Ph. D.). University of California, Berkeley. стр. 52. Docket 3331743.
- ^ Jackson 1975
- ^ Griffiths, David J (1999). Introduction to electrodynamics (Third изд.). Prentice Hall. ISBN 978-0-13-805326-0.
- ^ Hampshire, Damian P. (29. 10. 2018). „A derivation of Maxwell's equations using the Heaviside notation”. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 376 (2134). Bibcode:2018RSPTA.37670447H. ISSN 1364-503X. PMC 6232579
 . PMID 30373937. arXiv:1510.04309
. PMID 30373937. arXiv:1510.04309  . doi:10.1098/rsta.2017.0447.
. doi:10.1098/rsta.2017.0447.
- ^ David J. Griffiths (1999). „4.2.2”. Introduction to Electrodynamics
 (third изд.). Prentice Hall. ISBN 9780138053260.
(third изд.). Prentice Hall. ISBN 9780138053260.
- ^ Morrison 1986
- ^ Littlejohn, Robert (јесен 2007). „Gaussian, SI and Other Systems of Units in Electromagnetic Theory” (PDF). Physics 221A, University of California, Berkeley lecture notes. Архивирано из оригинала (PDF) 11. 07. 2012. г. Приступљено 6. 5. 2008.
Литература[уреди | уреди извор]
- Griffiths, David J (1999). Introduction to electrodynamics (Third изд.). Prentice Hall. ISBN 978-0-13-805326-0.
- Jackson, J. D. (1975). Classical Electrodynamics (3rd изд.). ISBN 978-0-471-43132-9.
- Morrison, Ralph (1986). Grounding and Shielding Techniques in Instrumentation. Wiley-Interscience. ISBN 978-0-471-83805-0.
- Paul, Clayton R. (2001). Fundamentals of Electric Circuit Analysis. John Wiley & Sons. ISBN 978-0-471-37195-3.
- Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6th ed.). Brooks/Cole. ISBN 978-0-534-40842-8.
- Tipler, Paul (2004). Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics (5th ed.). W. H. Freeman. ISBN 978-0-7167-0810-0.
- Graham, Martin; Johnson, Howard (2002). High-speed signal propagation : advanced black magic (10. printing. изд.). Upper Saddle River, NJ: Prentice Hall PTR. ISBN 978-0-13-084408-8.
- Milton, Kimball; Schwinger, J. (18. 6. 2006). Electromagnetic Radiation: Variational Methods, Waveguides and Accelerators. Springer Science & Business Media. ISBN 978-3-540-29306-4.
Спољашње везе[уреди | уреди извор]
- Divider Circuits and Kirchhoff's Laws chapter from Lessons In Electric Circuits Vol 1 DC free ebook and Lessons In Electric Circuits series.






























