Коцка — разлика између измена
Исправљене словне грешке |
. |
||
| Ред 1: | Ред 1: | ||
{{Short description|Чврсти предмет са шест једнаких квадратних лица}} |
|||
{{друго значење2|Коцка}} |
{{друго значење2|Коцка}} |
||
[[Датотека:Hexahedron.gif|мини|200п|Коцка]] |
[[Датотека:Hexahedron.gif|мини|200п|Коцка]] |
||
'''Коцка''' (правилни хексаедар, од {{јез-грч|hexáedron}} - тело са шест површина) је један од пет [[Правилни полиедри|правилних полиедара]]. Омеђена је са шест страница, [[квадрат]]них [[површ]]и спојених тако да образују [[геометријско тело|тело]] са дванаест [[дуж]]и (ивица) и осам темена. Коцка је специјалан случај [[квадар|квадра]] коме су све странице једнаке. Посебне врсте коцке за играње јесу [[коцка (игра)|коцкице]] и [[Рубикова коцка]]. |
'''Коцка''' (правилни хексаедар, од {{јез-грч|hexáedron}} - тело са шест површина) је један од пет [[Правилни полиедри|правилних полиедара]]. Омеђена је са шест страница, [[квадрат]]них [[површ]]и спојених тако да образују [[геометријско тело|тело]] са дванаест [[дуж]]и (ивица) и осам темена. Коцка је специјалан случај [[квадар|квадра]] коме су све странице једнаке. Посебне врсте коцке за играње јесу [[коцка (игра)|коцкице]] и [[Рубикова коцка]]. |
||
| Ред 39: | Ред 41: | ||
|} |
|} |
||
== Ортогоналне пројекције == |
|||
== Напомене == |
|||
{{рут}} |
|||
The ''cube'' has four special [[orthogonal projection]]s, centered, on a vertex, edges, face and normal to its [[vertex figure]]. The first and third correspond to the A<sub>2</sub> and B<sub>2</sub> [[Coxeter plane]]s. |
|||
{|class=wikitable width=360 |
|||
|+ Orthogonal projections |
|||
|- |
|||
!Centered by |
|||
!Face |
|||
!Vertex |
|||
|- align=center |
|||
!Coxeter planes |
|||
|'''B<sub>2</sub>'''<BR>[[File:2-cube.svg|100px]] |
|||
|'''A<sub>2</sub>'''<BR>[[File:3-cube t0.svg|100px]] |
|||
|- align=center |
|||
!Projective<BR>symmetry |
|||
|[4] |
|||
|[6] |
|||
|- |
|||
!Tilted views |
|||
|[[File:Cube t0 e.png|100px]] |
|||
|[[File:Cube t0 fb.png|100px]] |
|||
|} |
|||
== Сферно поплочавање == |
|||
The cube can also be represented as a [[spherical tiling]], and projected onto the plane via a [[stereographic projection]]. This projection is [[Conformal map|conformal]], preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane. |
|||
{|class=wikitable |
|||
|- align=center valign=top |
|||
|[[File:Uniform tiling 432-t0.png|160px]] |
|||
|[[File:Cube stereographic projection.svg|160px]] |
|||
|- |
|||
![[Orthographic projection]] |
|||
![[Stereographic projection]] |
|||
|} |
|||
== Декартове координате == |
|||
For a cube centered at the origin, with edges parallel to the axes and with an edge length of 2, the [[Cartesian coordinates]] of the vertices are |
|||
:(±1, ±1, ±1) |
|||
while the interior consists of all points (''x''<sub>0</sub>, ''x''<sub>1</sub>, ''x''<sub>2</sub>) with −1 < ''x''<sub>''i''</sub> < 1 for all ''i''. |
|||
== Уједначене боје и симетрија == |
|||
[[File:Octahedral subgroup tree.png|thumb|[[Octahedral symmetry]] tree]] |
|||
The cube has three uniform colorings, named by the colors of the square faces around each vertex: 111, 112, 123. |
|||
The cube has four classes of symmetry, which can be represented by [[vertex-transitive]] coloring the faces. The highest octahedral symmetry O<sub>h</sub> has all the faces the same color. The [[Dihedral symmetry in three dimensions|dihedral symmetry]] D<sub>4h</sub> comes from the cube being a solid, with all the six sides being different colors. The prismatic subsets D<sub>2d</sub> has the same coloring as the previous one and D<sub>2h</sub> has alternating colors for its sides for a total of three colors, paired by opposite sides. Each symmetry form has a different [[Wythoff symbol]]. |
|||
{|class="wikitable" |
|||
|- align=center |
|||
!Name |
|||
!Regular<BR>hexahedron |
|||
!Square prism |
|||
!Rectangular<BR>trapezoprism |
|||
![[Rectangular cuboid|Rectangular<BR>cuboid]] |
|||
![[Rhombus|Rhombic]]<BR>prism |
|||
!Trigonal<BR>[[trapezohedron]] |
|||
|- align=center |
|||
![[Coxeter-Dynkin diagram|Coxeter<BR>diagram]] |
|||
|{{CDD|node_1|4|node|3|node}} |
|||
|{{CDD|node_1|4|node|2|node_1}} |
|||
|{{CDD|node_1|4|node_h|2x|node_h}} |
|||
|{{CDD|node_1|2|node_1|2|node_1}} |
|||
|{{CDD|node_1|2|node_f1|2x|node_f1}} |
|||
|{{CDD|node_fh|2x|node_fh|6|node}} |
|||
|- align=center |
|||
![[Schläfli symbol|Schläfli<BR>symbol]] |
|||
|{4,3} |
|||
|{4}×{ }<BR>rr{4,2} |
|||
|s<sub>2</sub>{2,4} |
|||
|{ }<sup>3</sup><BR>tr{2,2} |
|||
|{ }×2{ } |
|||
| |
|||
|- align=center |
|||
![[Wythoff symbol|Wythoff<BR>symbol]] |
|||
|3 | 4 2 |
|||
|4 2 | 2 |
|||
| |
|||
|2 2 2 | |
|||
| |
|||
| |
|||
|- align=center |
|||
![[List of spherical symmetry groups|Symmetry]] |
|||
|O<sub>h</sub><br>[4,3]<BR>(*432) |
|||
|D<sub>4h</sub><br>[4,2]<BR>(*422) |
|||
|D<sub>2d</sub><br>[4,2<sup>+</sup>]<BR>(2*2) |
|||
|colspan=2|D<sub>2h</sub><br>[2,2]<BR>(*222) |
|||
|D<sub>3d</sub><br>[6,2<sup>+</sup>]<BR>(2*3) |
|||
|- align=center |
|||
!Symmetry<BR>order |
|||
|24 |
|||
|16 |
|||
|8 |
|||
|colspan=2|8 |
|||
|12 |
|||
|- align=center |
|||
!Image<br>(uniform<BR>coloring) |
|||
|[[Image:Hexahedron.png|80px]]<br>(111) |
|||
|[[Image:Tetragonal prism.png|80px]]<br>(112) |
|||
|[[File:Cube rotorotational symmetry.png|80px]]<BR>(112) |
|||
|[[Image:Uniform polyhedron 222-t012.png|80px]]<br>(123) |
|||
|[[File:Cube_rhombic_symmetry.png|80px]]<BR>(112) |
|||
|[[File:Trigonal trapezohedron.png|80px]]<br>(111), (112) |
|||
|} |
|||
== Геометријски односи == |
|||
[[File:The 11 cubic nets.svg|thumb|250px|right|The 11 nets of the cube.]] |
|||
[[File:Stone Dice 17.JPG|right|thumb|150px|These familiar six-sided [[dice]] are cube-shaped.]] |
|||
A cube has eleven [[net (polyhedron)|nets]] (one shown above): that is, there are eleven ways to flatten a hollow cube by cutting seven edges.<ref>{{mathworld |urlname=Cube |title=Cube}}</ref> To color the cube so that no two adjacent faces have the same color, one would need at least three colors. |
|||
The cube is the cell of [[cubic honeycomb|the only regular tiling of three-dimensional Euclidean space]]. It is also unique among the Platonic solids in having faces with an even number of sides and, consequently, it is the only member of that group that is a [[zonohedron]] (every face has point symmetry). |
|||
The cube can be cut into six identical [[square pyramid]]s. If these square pyramids are then attached to the faces of a second cube, a [[rhombic dodecahedron]] is obtained (with pairs of coplanar triangles combined into rhombic faces). |
|||
== Повезани полиедри == |
|||
[[Image:Dual Cube-Octahedron.svg|thumb|200px|right|The dual of a cube is an [[octahedron]], seen here with vertices at the center of the cube's square faces.]] |
|||
[[File:Hemicube.svg|200px|thumb|The [[Hemicube (geometry)|hemicube]] is the 2-to-1 quotient of the cube.]] |
|||
The quotient of the cube by the [[Antipodal point|antipodal]] map yields a [[projective polyhedron]], the [[Hemicube (geometry)|hemicube]]. |
|||
If the original cube has edge length 1, its [[dual polyhedron]] (an [[octahedron]]) has edge length <math>\scriptstyle \sqrt{2}/2</math>. |
|||
The cube is a special case in various classes of general polyhedra: |
|||
{|class=wikitable |
|||
!Name!!Equal edge-lengths?!!Equal angles?!!Right angles? |
|||
|- |
|||
|'''Cube'''||'''Yes'''||'''Yes'''||'''Yes''' |
|||
|- |
|||
|[[Rhombohedron]]||Yes||Yes||No |
|||
|- |
|||
|[[Cuboid]]||No||Yes||Yes |
|||
|- |
|||
|[[Parallelepiped]]||No||Yes||No |
|||
|- |
|||
|[[quadrilateral]]ly faced hexahedron||No||No||No |
|||
|} |
|||
The vertices of a cube can be grouped into two groups of four, each forming a regular [[tetrahedron]]; more generally this is referred to as a [[demicube]]. These two together form a regular [[polyhedral compound|compound]], the [[stella octangula]]. The intersection of the two forms a regular octahedron. The symmetries of a regular tetrahedron correspond to those of a cube which map each tetrahedron to itself; the other symmetries of the cube map the two to each other. |
|||
===In uniform honeycombs and polychora=== |
|||
It is an element of 9 of 28 [[convex uniform honeycomb]]s: |
|||
{|class=wikitable width=500 |
|||
|- align=center valign=top |
|||
|[[Cubic honeycomb]]<br>{{CDD|node_1|4|node|3|node|4|node}}<br>{{CDD|node_1|4|node|4|node|2|node_1|infin|node}} |
|||
|[[Truncated square prismatic honeycomb]]<br>{{CDD|node_1|4|node_1|4|node|2|node_1|infin|node}} |
|||
|[[Snub square prismatic honeycomb]]<br>{{CDD|node_h|4|node_h|4|node_h|2|node_1|infin|node}} |
|||
|[[Elongated triangular prismatic honeycomb]] |
|||
|[[Gyroelongated triangular prismatic honeycomb]] |
|||
|- align=center |
|||
|[[File:Partial cubic honeycomb.png|100px]] |
|||
|[[File:Truncated square prismatic honeycomb.png|100px]] |
|||
|[[File:Snub square prismatic honeycomb.png|100px]] |
|||
|[[File:Elongated triangular prismatic honeycomb.png|100px]] |
|||
|[[File:Gyroelongated triangular prismatic honeycomb.png|100px]] |
|||
|- align=center |
|||
|[[Cantellated cubic honeycomb]]<br>{{CDD|node|4|node_1|3|node|4|node_1}} |
|||
|[[Cantitruncated cubic honeycomb]]<br>{{CDD|node|4|node_1|3|node_1|4|node_1}} |
|||
|[[Runcitruncated cubic honeycomb]]<br>{{CDD|node_1|4|node|3|node_1|4|node_1}} |
|||
|[[Runcinated alternated cubic honeycomb]]<br>{{CDD|nodes_10ru|split2|node|4|node_1}} |
|||
|- align=center |
|||
|[[File:HC A5-A3-P2.png|100px]] |
|||
|[[File:HC A6-A4-P2.png|100px]] |
|||
|[[File:HC A5-A2-P2-Pr8.png|100px]] |
|||
|[[File:HC A5-P2-P1.png|100px]] |
|||
|} |
|||
It is also an element of five four-dimensional [[uniform polychora]]: |
|||
{|class=wikitable width=500 |
|||
|- align=center |
|||
|[[Tesseract]]<br>{{CDD|node_1|4|node|3|node|3|node}} |
|||
|[[Cantellated 16-cell]]<br>{{CDD|node|4|node_1|3|node|3|node_1}} |
|||
|[[Runcinated tesseract]]<br>{{CDD|node_1|4|node|3|node|3|node_1}} |
|||
|[[Cantitruncated 16-cell]]<br>{{CDD|node|4|node_1|3|node_1|3|node_1}} |
|||
|[[Runcitruncated 16-cell]]<br>{{CDD|node_1|4|node|3|node_1|3|node_1}} |
|||
|- align=center |
|||
|[[File:4-cube t0.svg|100px]] |
|||
|[[File:24-cell t1 B4.svg|100px]] |
|||
|[[File:4-cube t03.svg|100px]] |
|||
|[[File:4-cube t123.svg|100px]] |
|||
|[[File:4-cube t023.svg|100px]] |
|||
|} |
|||
== Референце == |
|||
{{reflist}} |
{{reflist}} |
||
== Литература == |
|||
{{Refbegin|30em}} |
|||
* {{cite book | author= Anthony Pugh | year= 1976 | title= Polyhedra: A visual approach | publisher= University of California Press Berkeley | location= California | isbn= 0-520-03056-7 }} |
|||
* Љиљана Петрушевски - Полиедри |
|||
* Cromwell, P.;''Polyhedra'', CUP hbk (1997), pbk. (1999). |
|||
* {{cite book| author1 = Grünbaum, B. | authorlink1 = Branko Grünbaum | chapter = Polyhedra with Hollow Faces |
|||
| editor1 = Tibor Bisztriczky | editor2 = Peter McMullen |
|||
| editor3 = Rolf Schneider |display-editors = 3 | editor4 = A Weiss |
|||
| title = Proceedings of the NATO Advanced Study Institute on Polytopes: Abstract, Convex and Computational |
|||
| year = 1994| publisher = Springer | location = |isbn= 978-94-010-4398-4| pages = 43–70 |
|||
| url = http://link.springer.com/chapter/10.1007/978-94-011-0924-6_3}} |
|||
* Grünbaum, B.; Are your polyhedra the same as my polyhedra? ''Discrete and comput. geom: the Goodman-Pollack festschrift'', ed. Aronov et al. Springer (2003) pp. 461–488.'' ([http://www.math.washington.edu/~grunbaum/Your%20polyhedra-my%20polyhedra.pdf pdf] {{Wayback|url=http://www.math.washington.edu/~grunbaum/Your%20polyhedra-my%20polyhedra.pdf |date=20160803160413 }}) |
|||
* [[Joseph Louis François Bertrand|Bertrand, J.]] (1858). Note sur la théorie des polyèdres réguliers, ''Comptes rendus des séances de l'Académie des Sciences'', '''46''', pp. 79–82. |
|||
* Haeckel, E. (1904). ''[[Kunstformen der Natur]]''. Available as Haeckel, E. ''Art forms in nature'', Prestel USA (1998), {{isbn|3-7913-1990-6}}, or online at https://web.archive.org/web/20090627082453/http://caliban.mpiz-koeln.mpg.de/~stueber/haeckel/kunstformen/natur.html |
|||
*Smith, J. V. (1982). ''Geometrical And Structural Crystallography''. John Wiley and Sons. |
|||
* [[Duncan MacLaren Young Sommerville|Sommerville, D. M. Y.]] (1930). ''An Introduction to the Geometry of n Dimensions.'' E. P. Dutton, New York. (Dover Publications edition, 1958). Chapter X: The Regular Polytopes. |
|||
*[[H.S.M. Coxeter|Coxeter, H.S.M.]]; Regular Polytopes (third edition). Dover Publications Inc. {{isbn|0-486-61480-8}} |
|||
* {{cite journal |authorlink=Hassler Whitney |first=Hassler |last=Whitney |title=Congruent graphs and the connectivity of graphs |url=https://archive.org/details/sim_american-journal-of-mathematics_1932-01_54_1/page/150 |journal=Amer. J. Math. |volume=54 |issue=1 |pages=150–168 |year=1932 |jstor=2371086 |doi=10.2307/2371086|hdl=10338.dmlcz/101067 }} |
|||
* {{citation |
|||
| last1 = Blind | first1 = Roswitha |
|||
| last2 = Mani-Levitska | first2 = Peter |
|||
| doi = 10.1007/BF01830678 |
|||
| issue = 2–3 |
|||
| journal = [[Aequationes Mathematicae]] |
|||
| mr = 921106 |
|||
| pages = 287–297 |
|||
| title = Puzzles and polytope isomorphisms |
|||
| volume = 34 |
|||
| year = 1987}} |
|||
* {{citation |
|||
| last = Kalai | first = Gil | authorlink = Gil Kalai |
|||
| doi = 10.1016/0097-3165(88)90064-7 |
|||
| issue = 2 |
|||
| journal = [[Journal of Combinatorial Theory]] | series = Ser. A |
|||
| mr = 964396 |
|||
| pages = 381–383 |
|||
| title = A simple way to tell a simple polytope from its graph |
|||
| volume = 49 |
|||
| year = 1988}} |
|||
* {{cite journal |first=Volker |last=Kaibel |first2=Alexander |last2=Schwartz |url=http://eprintweb.org/S/authors/All/ka/Kaibel/16 |title=On the Complexity of Polytope Isomorphism Problems |journal=[[Graphs and Combinatorics]] |volume=19 |issue=2 |pages=215–230 |year=2003 |arxiv=math/0106093 |doi=10.1007/s00373-002-0503-y |url-status=dead |archiveurl=https://web.archive.org/web/20150721175904/http://eprintweb.org/S/authors/All/ka/Kaibel/16 |archivedate=2015-07-21 }} |
|||
* {{Cite book | last1 = Büeler | first1 = B. | last2 = Enge | first2 = A. | last3 = Fukuda | first3 = K. | doi = 10.1007/978-3-0348-8438-9_6 | chapter = Exact Volume Computation for Polytopes: A Practical Study | title = Polytopes — Combinatorics and Computation | pages = 131 | year = 2000 | isbn = 978-3-7643-6351-2 | pmid = | pmc = }} |
|||
* {{citation |
|||
| last = Yao | first = Andrew Chi Chih | authorlink = Andrew Yao |
|||
| doi = 10.1145/322276.322289 |
|||
| issue = 4 |
|||
| journal = [[Journal of the ACM]] |
|||
| mr = 677089 |
|||
| pages = 780–787 |
|||
| title = A lower bound to finding convex hulls |
|||
| volume = 28 |
|||
| year = 1981}}; {{citation |
|||
| last = Ben-Or | first = Michael |
|||
| contribution = Lower Bounds for Algebraic Computation Trees |
|||
| doi = 10.1145/800061.808735 |
|||
| pages = 80–86 |
|||
| title = Proceedings of the Fifteenth Annual ACM Symposium on Theory of Computing (STOC '83) |
|||
| year = 1983}} |
|||
* {{citation |
|||
| last1 = Cundy | first1 = H. Martyn | author1-link = Martyn Cundy |
|||
| last2 = Rollett | first2 = A. P. |
|||
| edition = 2nd |
|||
| location = Oxford |
|||
| mr = 0124167 |
|||
| publisher = Clarendon Press |
|||
| title = Mathematical Models |
|||
| year = 1961}}. |
|||
* {{citation |
|||
| last1 = Gailiunas | first1 = P. |
|||
| last2 = Sharp | first2 = J. |
|||
| doi = 10.1080/00207390500064049 |
|||
| issue = 6 |
|||
| journal = International Journal of Mathematical Education in Science and Technology |
|||
| pages = 617–642 |
|||
| title = Duality of polyhedra |
|||
| volume = 36 |
|||
| year = 2005}}. |
|||
* {{citation |
|||
| last = Grünbaum | first = Branko | authorlink = Branko Grünbaum |
|||
| editor1-last = Aronov | editor1-first = Boris | editor1-link = Boris Aronov |
|||
| editor2-last = Basu | editor2-first = Saugata |
|||
| editor3-last = Pach | editor3-first = János | editor3-link = János Pach |
|||
| editor4-last = Sharir | editor4-first = Micha | editor4-link = Micha Sharir |
|||
| contribution = Are your polyhedra the same as my polyhedra? |
|||
| doi = 10.1007/978-3-642-55566-4_21 |
|||
| mr = 2038487 |
|||
| pages = 461–488 |
|||
| publisher = Springer | location = Berlin |
|||
| series = Algorithms and Combinatorics |
|||
| title = Discrete and Computational Geometry: The Goodman–Pollack Festschrift |
|||
| volume = 25 |
|||
| year = 2003| citeseerx = 10.1.1.102.755| isbn = 978-3-642-62442-1 }}. |
|||
* {{citation |
|||
| last = Grünbaum | first = Branko | authorlink = Branko Grünbaum |
|||
| doi = 10.1016/j.disc.2005.09.037 |
|||
| issue = 3–5 |
|||
| journal = [[Discrete Mathematics (journal)|Discrete Mathematics]] |
|||
| mr = 2287486 |
|||
| pages = 445–463 |
|||
| title = Graphs of polyhedra; polyhedra as graphs |
|||
| volume = 307 |
|||
| year = 2007}}. |
|||
* {{citation |
|||
| last1 = Grünbaum | first1 = Branko | author1-link = Branko Grünbaum |
|||
| last2 = Shephard | first2 = G. C. | author2-link = Geoffrey Colin Shephard |
|||
| editor-last = Senechal | editor-first = Marjorie | editor-link = Marjorie Senechal |
|||
| contribution = Duality of polyhedra |
|||
| doi = 10.1007/978-0-387-92714-5_15 |
|||
| isbn = 978-0-387-92713-8 |
|||
| mr = 3077226 |
|||
| pages = 211–216 |
|||
| publisher = Springer | location = New York |
|||
| title = Shaping Space: Exploring polyhedra in nature, art, and the geometrical imagination |
|||
| year = 2013}}. |
|||
* {{citation| first=Magnus | last=Wenninger | authorlink=Magnus Wenninger | title=Dual Models | publisher=Cambridge University Press | year=1983 | isbn=0-521-54325-8 | mr = 0730208}}. |
|||
* {{citation |
|||
| last1 = Barvinok | first1 = Alexander |
|||
| isbn = 0821829688 |
|||
| publisher = American Mathematical Soc. | location = Providence |
|||
| title = A course in convexity |
|||
| year = 2002}} |
|||
{{refend}} |
|||
== Спољашње везе == |
== Спољашње везе == |
||
{{Commonscat|Cube}} |
{{Commonscat|Cube}} |
||
*{{mathworld |urlname=Cube |title=Cube}} |
|||
*[https://web.archive.org/web/20071009235233/http://polyhedra.org/poly/show/1/cube Cube: Interactive Polyhedron Model]* |
|||
*[http://www.mathopenref.com/cubevolume.html Volume of a cube], with interactive animation |
|||
*[http://www.software3d.com/Cube.php Cube] (Robert Webb's site) |
|||
{{полиедри}} |
{{полиедри}} |
||
Верзија на датум 20. јул 2022. у 20:49

Коцка (правилни хексаедар, од грч. hexáedron - тело са шест површина) је један од пет правилних полиедара. Омеђена је са шест страница, квадратних површи спојених тако да образују тело са дванаест дужи (ивица) и осам темена. Коцка је специјалан случај квадра коме су све странице једнаке. Посебне врсте коцке за играње јесу коцкице и Рубикова коцка.
Уопштење
Коцка K у простору Rn се може дефинисати помоћу једне тачке A = (a1, ..., an) из Rn, дужине ивице коцке a, као и са n вектора v1, ..., vn који чине једну позитивно оријентисану ортонормирану базу Rn. Рецимо да је свака ивица коцке K паралелна са тачно једним различитим вектором те базе, као и да тачка A представља почетак координатног система кога граде ови вектори.
Свака тачка X = (x1, ..., xn) коцке K онда може бити представљена на следећи начин:
Уколико се за векторе v1, ..., vn узму вектори који чине канонску базу Rn, добија се:
Формуле
Следе неке од чешће коришћених формула које се везују за коцку.

| Површина | |
| Запремина | |
| Мала дијагонала[1] | |
| Велика дијагонала | |
| Полупречник уписане сфере | |
| Полупречник описане сфере |
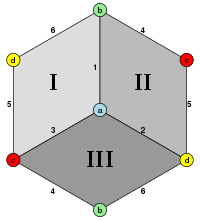
Ортогоналне пројекције
Један корисник управо ради на овом чланку. Молимо остале кориснике да му допусте да заврши са радом. Ако имате коментаре и питања у вези са чланком, користите страницу за разговор.
Хвала на стрпљењу. Када радови буду завршени, овај шаблон ће бити уклоњен. Напомене
|
The cube has four special orthogonal projections, centered, on a vertex, edges, face and normal to its vertex figure. The first and third correspond to the A2 and B2 Coxeter planes.
| Centered by | Face | Vertex |
|---|---|---|
| Coxeter planes | B2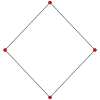
|
A2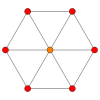
|
| Projective symmetry |
[4] | [6] |
| Tilted views | 
|

|
Сферно поплочавање
The cube can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.

|

|
| Orthographic projection | Stereographic projection |
|---|
Декартове координате
For a cube centered at the origin, with edges parallel to the axes and with an edge length of 2, the Cartesian coordinates of the vertices are
- (±1, ±1, ±1)
while the interior consists of all points (x0, x1, x2) with −1 < xi < 1 for all i.
Уједначене боје и симетрија

The cube has three uniform colorings, named by the colors of the square faces around each vertex: 111, 112, 123.
The cube has four classes of symmetry, which can be represented by vertex-transitive coloring the faces. The highest octahedral symmetry Oh has all the faces the same color. The dihedral symmetry D4h comes from the cube being a solid, with all the six sides being different colors. The prismatic subsets D2d has the same coloring as the previous one and D2h has alternating colors for its sides for a total of three colors, paired by opposite sides. Each symmetry form has a different Wythoff symbol.
| Name | Regular hexahedron |
Square prism | Rectangular trapezoprism |
Rectangular cuboid |
Rhombic prism |
Trigonal trapezohedron |
|---|---|---|---|---|---|---|
| Coxeter diagram |
||||||
| Schläfli symbol |
{4,3} | {4}×{ } rr{4,2} |
s2{2,4} | { }3 tr{2,2} |
{ }×2{ } | |
| Wythoff symbol |
3 | 4 2 | 4 2 | 2 | 2 2 2 | | |||
| Symmetry | Oh [4,3] (*432) |
D4h [4,2] (*422) |
D2d [4,2+] (2*2) |
D2h [2,2] (*222) |
D3d [6,2+] (2*3) | |
| Symmetry order |
24 | 16 | 8 | 8 | 12 | |
| Image (uniform coloring) |
 (111) |
 (112) |
 (112) |
 (123) |
 (112) |
 (111), (112) |
Геометријски односи


A cube has eleven nets (one shown above): that is, there are eleven ways to flatten a hollow cube by cutting seven edges.[2] To color the cube so that no two adjacent faces have the same color, one would need at least three colors.
The cube is the cell of the only regular tiling of three-dimensional Euclidean space. It is also unique among the Platonic solids in having faces with an even number of sides and, consequently, it is the only member of that group that is a zonohedron (every face has point symmetry).
The cube can be cut into six identical square pyramids. If these square pyramids are then attached to the faces of a second cube, a rhombic dodecahedron is obtained (with pairs of coplanar triangles combined into rhombic faces).
Повезани полиедри

The quotient of the cube by the antipodal map yields a projective polyhedron, the hemicube.
If the original cube has edge length 1, its dual polyhedron (an octahedron) has edge length .
The cube is a special case in various classes of general polyhedra:
| Name | Equal edge-lengths? | Equal angles? | Right angles? |
|---|---|---|---|
| Cube | Yes | Yes | Yes |
| Rhombohedron | Yes | Yes | No |
| Cuboid | No | Yes | Yes |
| Parallelepiped | No | Yes | No |
| quadrilaterally faced hexahedron | No | No | No |
The vertices of a cube can be grouped into two groups of four, each forming a regular tetrahedron; more generally this is referred to as a demicube. These two together form a regular compound, the stella octangula. The intersection of the two forms a regular octahedron. The symmetries of a regular tetrahedron correspond to those of a cube which map each tetrahedron to itself; the other symmetries of the cube map the two to each other.
In uniform honeycombs and polychora
It is an element of 9 of 28 convex uniform honeycombs:
It is also an element of five four-dimensional uniform polychora:
| Tesseract |
Cantellated 16-cell |
Runcinated tesseract |
Cantitruncated 16-cell |
Runcitruncated 16-cell |

|

|
|

|

|
Референце
Литература
- Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7.
- Љиљана Петрушевски - Полиедри
- Cromwell, P.;Polyhedra, CUP hbk (1997), pbk. (1999).
- Grünbaum, B. (1994). „Polyhedra with Hollow Faces”. Ур.: Tibor Bisztriczky; Peter McMullen; Rolf Schneider; et al. Proceedings of the NATO Advanced Study Institute on Polytopes: Abstract, Convex and Computational. Springer. стр. 43—70. ISBN 978-94-010-4398-4.
- Grünbaum, B.; Are your polyhedra the same as my polyhedra? Discrete and comput. geom: the Goodman-Pollack festschrift, ed. Aronov et al. Springer (2003) pp. 461–488. (pdf Архивирано на сајту Wayback Machine (3. август 2016))
- Bertrand, J. (1858). Note sur la théorie des polyèdres réguliers, Comptes rendus des séances de l'Académie des Sciences, 46, pp. 79–82.
- Haeckel, E. (1904). Kunstformen der Natur. Available as Haeckel, E. Art forms in nature, Prestel USA (1998), ISBN 3-7913-1990-6, or online at https://web.archive.org/web/20090627082453/http://caliban.mpiz-koeln.mpg.de/~stueber/haeckel/kunstformen/natur.html
- Smith, J. V. (1982). Geometrical And Structural Crystallography. John Wiley and Sons.
- Sommerville, D. M. Y. (1930). An Introduction to the Geometry of n Dimensions. E. P. Dutton, New York. (Dover Publications edition, 1958). Chapter X: The Regular Polytopes.
- Coxeter, H.S.M.; Regular Polytopes (third edition). Dover Publications Inc. ISBN 0-486-61480-8
- Whitney, Hassler (1932). „Congruent graphs and the connectivity of graphs”. Amer. J. Math. 54 (1): 150—168. JSTOR 2371086. doi:10.2307/2371086. hdl:10338.dmlcz/101067.
- Blind, Roswitha; Mani-Levitska, Peter (1987), „Puzzles and polytope isomorphisms”, Aequationes Mathematicae, 34 (2–3): 287—297, MR 921106, doi:10.1007/BF01830678
- Kalai, Gil (1988), „A simple way to tell a simple polytope from its graph”, Journal of Combinatorial Theory, Ser. A, 49 (2): 381—383, MR 964396, doi:10.1016/0097-3165(88)90064-7
- Kaibel, Volker; Schwartz, Alexander (2003). „On the Complexity of Polytope Isomorphism Problems”. Graphs and Combinatorics. 19 (2): 215—230. arXiv:math/0106093
 . doi:10.1007/s00373-002-0503-y. Архивирано из оригинала 2015-07-21. г.
. doi:10.1007/s00373-002-0503-y. Архивирано из оригинала 2015-07-21. г. - Büeler, B.; Enge, A.; Fukuda, K. (2000). „Exact Volume Computation for Polytopes: A Practical Study”. Polytopes — Combinatorics and Computation. стр. 131. ISBN 978-3-7643-6351-2. doi:10.1007/978-3-0348-8438-9_6.
- Yao, Andrew Chi Chih (1981), „A lower bound to finding convex hulls”, Journal of the ACM, 28 (4): 780—787, MR 677089, doi:10.1145/322276.322289; Ben-Or, Michael (1983), „Lower Bounds for Algebraic Computation Trees”, Proceedings of the Fifteenth Annual ACM Symposium on Theory of Computing (STOC '83), стр. 80—86, doi:10.1145/800061.808735
- Cundy, H. Martyn; Rollett, A. P. (1961), Mathematical Models (2nd изд.), Oxford: Clarendon Press, MR 0124167.
- Gailiunas, P.; Sharp, J. (2005), „Duality of polyhedra”, International Journal of Mathematical Education in Science and Technology, 36 (6): 617—642, doi:10.1080/00207390500064049.
- Grünbaum, Branko (2003), „Are your polyhedra the same as my polyhedra?”, Ур.: Aronov, Boris; Basu, Saugata; Pach, János; Sharir, Micha, Discrete and Computational Geometry: The Goodman–Pollack Festschrift, Algorithms and Combinatorics, 25, Berlin: Springer, стр. 461—488, CiteSeerX 10.1.1.102.755
 , ISBN 978-3-642-62442-1, MR 2038487, doi:10.1007/978-3-642-55566-4_21.
, ISBN 978-3-642-62442-1, MR 2038487, doi:10.1007/978-3-642-55566-4_21. - Grünbaum, Branko (2007), „Graphs of polyhedra; polyhedra as graphs”, Discrete Mathematics, 307 (3–5): 445—463, MR 2287486, doi:10.1016/j.disc.2005.09.037.
- Grünbaum, Branko; Shephard, G. C. (2013), „Duality of polyhedra”, Ур.: Senechal, Marjorie, Shaping Space: Exploring polyhedra in nature, art, and the geometrical imagination, New York: Springer, стр. 211—216, ISBN 978-0-387-92713-8, MR 3077226, doi:10.1007/978-0-387-92714-5_15.
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 0-521-54325-8, MR 0730208.
- Barvinok, Alexander (2002), A course in convexity, Providence: American Mathematical Soc., ISBN 0821829688
Спољашње везе
- Weisstein, Eric W. „Cube”. MathWorld.
- Cube: Interactive Polyhedron Model*
- Volume of a cube, with interactive animation
- Cube (Robert Webb's site)

![{\displaystyle X:A+\sum _{k=1}^{n}{\alpha _{k}\cdot v_{k}},\;\alpha _{k}\in [0,a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/380751fa9a749c3c609e8846bc9c586d879f2f3c)
![{\displaystyle X:\{x_{i}\in [a_{i},a_{i}+a],\;i=1,...,n\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a7ba7957df315f44f34500dc4ec4d2b7277d41c)