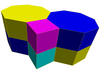
Коцка

Коцка (правилни хексаедар, од грч. hexáedron - тело са шест површина) је један од пет правилних полиедара. Омеђена је са шест страница, квадратних површи спојених тако да образују тело са дванаест дужи (ивица) и осам темена. Коцка је специјалан случај квадра коме су све странице једнаке. Посебне врсте коцке за играње јесу коцкице и Рубикова коцка.

Уопштење[уреди | уреди извор]

Коцка K у простору Rⁿ се може дефинисати помоћу једне тачке A = (a₁, ..., a_n) из Rⁿ, дужине ивице коцке a, као и са n вектора v₁, ..., v_n који чине једну позитивно оријентисану ортонормирану базу Rⁿ. Рецимо да је свака ивица коцке K паралелна са тачно једним различитим вектором те базе, као и да тачка A представља почетак координатног система кога граде ови вектори.

Свака тачка X = (x₁, ..., x_n) коцке K онда може бити представљена на следећи начин:

X:A+\sum _{k=1}^{n}{\alpha _{k}\cdot v_{k}},\;\alpha _{k}\in [0,a]

Уколико се за векторе v₁, ..., v_n узму вектори који чине канонску базу Rⁿ, добија се:

X:\{x_{i}\in [a_{i},a_{i}+a],\;i=1,...,n\}

Формуле[уреди | уреди извор]

Следе неке од чешће коришћених формула које се везују за коцку.

Важнији елементи коцке

Површина	$P=6a^{2}\,$
Запремина	$V=a^{3}\,$
Мала дијагонала^[1]	$d=a{\sqrt {2}}$
Велика дијагонала	$D=a{\sqrt {3}}$
Полупречник уписане сфере	$r_{u}={\frac {a}{2}}$
Полупречник описане сфере	$r_{o}={\frac {D}{2}}=a{\frac {\sqrt {3}}{2}}$

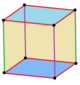
Ортогоналне пројекције[уреди | уреди извор]

Коцка има четири посебне ортогоналне пројекције, центриране, на темену, ивицама, лицу и нормално на њену фигуру темена. Први и трећи одговарају A₂ и B₂ Коксетеровим равнима.

Ортогоналне пројекције
Центриране са	Лице	Теме
Коксетерове равни	B₂	A₂
Пројективноа симетрија	[4]	[6]
Нагнути погледи

Сферно поплочавање[уреди | уреди извор]

Коцка се такође може представити као сферна плочица, и пројектована на раван путем стереографске пројекције. Ова пројекција је конформна, чува углове, али не и површине или дужине. Праве на сфери се пројектују као кружни лукови на раван.

Ортографска пројекција	Стереографска пројекција

Декартове координате[уреди | уреди извор]

За коцку са центром у координатном пореклу, са ивицама паралелним са осама и са дужином ивице од 2, картезијанске координате врхова су

(±1, ±1, ±1)

док се унутрашњост састоји од свих тачака (x₀, x₁, x₂) са −1 < x_i < 1 за свако i.

Уједначене боје и симетрија[уреди | уреди извор]

Стабло октаедарске симетрије

Коцка има три уједначене обојења, назване бојама квадрата око сваког темена: 111, 112, 123.

Коцка има четири класе симетрије, које се могу представити темено-транзитивним бојењем лица. Највиша октаедарска симетрија O_h има сва лица исте боје. Диедрална симетрија D_4h долази од тога што је коцка чврста, са свих шест страна различите боје. Призматични подскуп D_2d има истo обојење као и претходни, а D_2h има наизменичне боје за своје стране за укупно три боје, упарене са супротних страна. Сваки облик симетрије има другачији Витофов симбол.

Име	Регуларни хексаедар	Квадратна призма	Правоугаона трапезопризма	Правоугаони кубоид	Ромбна призма	Тригонални трапезоедар
Коксетеров дијаграм
Шафлијев симбол	{4,3}	{4}×{ } rr{4,2}	s₂{2,4}	{ }³ tr{2,2}	{ }×2{ }
Вајтофов симбол	3 \| 4 2	4 2 \| 2		2 2 2 \|
Симетрија	O_h [4,3] (*432)	D_4h [4,2] (*422)	D_2d [4,2⁺] (2*2)	D_2h [2,2] (*222)		D_3d [6,2⁺] (2*3)
Ред симетрије	24	16	8	8		12
Слика (једнобразно обојење)	(111)	(112)	(112)	(123)	(112)	(111), (112)

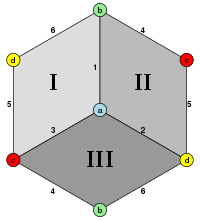
Геометријски односи[уреди | уреди извор]

Једанаест мрежа коцке.

Ове познате шестостране коцкице су кубоидног облика.

Коцка има једанаест мрежа (једна приказана изнад): то јест, постоји једанаест начина да се шупља коцка спљошти сечењем седам ивица.^[2] Да би се обојила коцку тако да ниједна суседна лица нема исту боју, требале би најмање три боје.

Коцка је ћелија јединог правилног поплочавања тродимензионалног еуклидског простора. Такође је јединствен међу Платоновим телима по томе што има лица са парним бројем страна и, сходно томе, једини је члан те групе који је зоноедар (свако лице има тачку симетрију).

Коцка се може исећи на шест идентичних квадратних пирамида. Ако се ове квадратне пирамиде затим причврсте на лица друге коцке, добија се ромбични додекаедар (са паровима компланарних троуглова комбинованих у ромбичне површине).

Повезани полиедри[уреди | уреди извор]

Дуал коцке је октаедар, који се овде види са врховима у центру квадратних страна коцке.

Хемикуб је коефицијент 2 према 1 коцке.

Количник коцке са Антиподалом мапом даје пројективни полиедар, хемикуб.

Ако оригинална коцка има дужину ивице 1, њен двоструки полиедар (октаедар) има дужину ивице $\scriptstyle {\sqrt {2}}/2$ .

Коцка је посебан случај у различитим класама општих полиедара:

Име	Једнаке дужине ивица?	Једнаки углови?	Прави углови?
Коцка	Да	Да	Да
Ромбоедар	Да	Да	Не
Кубоид	Не	Да	Да
Паралелепипед	Не	Да	Не
четвороугаоно окренут хексаедар\|Не	Не	Не

Темена коцке се могу груписати у две групе по четири, од којих свака формира правилан тетраедар; уопштеније, ово се назива демикуб. Ова два заједно формирају правилно спајање, стела октангула. Пресек ова два формира правилан октаедар. Симетрије правилног тетраедра одговарају симетрији коцке која сваки тетраедар пресликава на себе; остале симетрије коцке пресликавају то двоје једно на друго.

Једнолично саће и полихори[уреди | уреди извор]

То је елемент од 9 од 28 конвексног једноликог саћа:

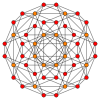
Кубично саће	Одсечено квадратно призматично саће	Окресани квадратно призматично саће	Издужено троугласто призматично саће	Жироиздужено троугласто призматично саће

Кантелирано кубно саће	Кантизарубљено кубично саће	Рансизарубљено кубично саће	Рансинирано наизменично кубично саће

Такође је елемент пет четвородимензионалних униформних полихора:

Тесеракт	Кантелирана 16-ћелија	Рансинирани тесеракт	Кантизарубљена 16-ћелија	Рансизарубљена 16-ћелија

Референце[уреди | уреди извор]

^ Некада се мала дијагонала обележава са d, а велика са D. Овде је мала обележена са d₁, а велика са d₂, да би се избегла вишезначност са теменом D.
^ Weisstein, Eric W. „Cube”. MathWorld.

Литература[уреди | уреди извор]

Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7.
Љиљана Петрушевски - Полиедри
Cromwell, P.;Polyhedra, CUP hbk (1997), pbk. (1999).
Grünbaum, B. (1994). „Polyhedra with Hollow Faces”. Ур.: Tibor Bisztriczky; Peter McMullen; Rolf Schneider; et al. Proceedings of the NATO Advanced Study Institute on Polytopes: Abstract, Convex and Computational. Springer. стр. 43—70. ISBN 978-94-010-4398-4.
Grünbaum, B.; Are your polyhedra the same as my polyhedra? Discrete and comput. geom: the Goodman-Pollack festschrift, ed. Aronov et al. Springer (2003) pp. 461–488. (pdf Архивирано на сајту Wayback Machine (3. август 2016))
Bertrand, J. (1858). Note sur la théorie des polyèdres réguliers, Comptes rendus des séances de l'Académie des Sciences, 46, pp. 79–82.
Haeckel, E. (1904). Kunstformen der Natur. Available as Haeckel, E. Art forms in nature, Prestel USA (1998), ISBN 3-7913-1990-6, or online at https://web.archive.org/web/20090627082453/http://caliban.mpiz-koeln.mpg.de/~stueber/haeckel/kunstformen/natur.html
Smith, J. V. (1982). Geometrical And Structural Crystallography. John Wiley and Sons.
Sommerville, D. M. Y. (1930). An Introduction to the Geometry of n Dimensions. E. P. Dutton, New York. (Dover Publications edition, 1958). Chapter X: The Regular Polytopes.
Coxeter, H.S.M.; Regular Polytopes (third edition). Dover Publications Inc. ISBN 0-486-61480-8
Whitney, Hassler (1932). „Congruent graphs and the connectivity of graphs”. Amer. J. Math. 54 (1): 150—168. JSTOR 2371086. doi:10.2307/2371086. hdl:10338.dmlcz/101067.
Blind, Roswitha; Mani-Levitska, Peter (1987), „Puzzles and polytope isomorphisms”, Aequationes Mathematicae, 34 (2–3): 287—297, MR 921106, doi:10.1007/BF01830678
Kalai, Gil (1988), „A simple way to tell a simple polytope from its graph”, Journal of Combinatorial Theory, Ser. A, 49 (2): 381—383, MR 964396, doi:10.1016/0097-3165(88)90064-7
Kaibel, Volker; Schwartz, Alexander (2003). „On the Complexity of Polytope Isomorphism Problems”. Graphs and Combinatorics. 19 (2): 215—230. arXiv:math/0106093 . doi:10.1007/s00373-002-0503-y. Архивирано из оригинала на датум 2015-07-21.
Büeler, B.; Enge, A.; Fukuda, K. (2000). „Exact Volume Computation for Polytopes: A Practical Study”. Polytopes — Combinatorics and Computation. стр. 131. ISBN 978-3-7643-6351-2. doi:10.1007/978-3-0348-8438-9_6.
Yao, Andrew Chi Chih (1981), „A lower bound to finding convex hulls”, Journal of the ACM, 28 (4): 780—787, MR 677089, doi:10.1145/322276.322289 ; Ben-Or, Michael (1983), „Lower Bounds for Algebraic Computation Trees”, Proceedings of the Fifteenth Annual ACM Symposium on Theory of Computing (STOC '83), стр. 80—86, doi:10.1145/800061.808735
Cundy, H. Martyn; Rollett, A. P. (1961), Mathematical Models (2nd изд.), Oxford: Clarendon Press, MR 0124167 .
Gailiunas, P.; Sharp, J. (2005), „Duality of polyhedra”, International Journal of Mathematical Education in Science and Technology, 36 (6): 617—642, doi:10.1080/00207390500064049 .
Grünbaum, Branko (2003), „Are your polyhedra the same as my polyhedra?”, Ур.: Aronov, Boris; Basu, Saugata; Pach, János; Sharir, Micha, Discrete and Computational Geometry: The Goodman–Pollack Festschrift, Algorithms and Combinatorics, 25, Berlin: Springer, стр. 461—488, CiteSeerX 10.1.1.102.755 , ISBN 978-3-642-62442-1, MR 2038487, doi:10.1007/978-3-642-55566-4_21 .
Grünbaum, Branko (2007), „Graphs of polyhedra; polyhedra as graphs”, Discrete Mathematics, 307 (3–5): 445—463, MR 2287486, doi:10.1016/j.disc.2005.09.037 .
Grünbaum, Branko; Shephard, G. C. (2013), „Duality of polyhedra”, Ур.: Senechal, Marjorie, Shaping Space: Exploring polyhedra in nature, art, and the geometrical imagination, New York: Springer, стр. 211—216, ISBN 978-0-387-92713-8, MR 3077226, doi:10.1007/978-0-387-92714-5_15 .
Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 0-521-54325-8, MR 0730208 .
Barvinok, Alexander (2002), A course in convexity, Providence: American Mathematical Soc., ISBN 0821829688

Спољашње везе[уреди | уреди извор]

Weisstein, Eric W. „Cube”. MathWorld.
Cube: Interactive Polyhedron Model*
Volume of a cube, with interactive animation
Cube (Robert Webb's site)

[1] Некада се мала дијагонала обележава са d, а велика са D. Овде је мала обележена са d₁, а велика са d₂, да би се избегла вишезначност са теменом D.

[2] Weisstein, Eric W. „Cube”. MathWorld.

[1]

[2]