Zlatni presek

${\frac {a+b}{a}}={\frac {a}{b}}$

Zlatni pravougaonik (u ružičastom) sa dužom stranom a i kraćom stranom side b, kada je postavljen pored kvadrata dužine a, proizvešće geometrijsku sličnost zlatnog pravougaonika sa dužom stranom a + b i kraćom stranom a. Ovo ilustruje odnos ${\frac {a+b}{a}}={\frac {a}{b}}\equiv \varphi$.

U matematici dve veličine su u zlatnom odnosu, ako je odnos između dve veličine jednak odnosu sume te dve vrednosti naspram veće vrednosti. Slika na desnoj strani ilustruje geometrijski odnos. Algebarski, za količine a i b i a > b > 0,

${\frac {a+b}{a}}={\frac {a}{b}}\ {\stackrel {\text{def}}{=}}\ \varphi ,$

grčko slovo fi ($\varphi$ ili $\phi$) predstavlja konstantu. Njena vrednost je:

$\varphi ={\frac {1+{\sqrt {5}}}{2}}=1.6180339887\ldots .$  A001622

Zlatni odnos ima i naziv zlatni presek (latinski: sectio aurea).. Ostali nazivi uključuju krajnja i srednja razmera, ekstremni odnos, središnji presek, zlatna proporcija, i zlatni broj. Sectio divina lat. (izgovor: sekcio divina). Božanstveni presjek. Ovaj odnos duži primjenjen na predmetima, slikama itd. izaziva poseban estetski doživljaj – dopadanje, pa otuda i naziv „Božanski presjek“.

Zlatni odnos se pojavljuje u nekim šablonima u prirodi, uključujući phyllotaxis (spiralno ređanje listova) i u drugim delovima biljaka.

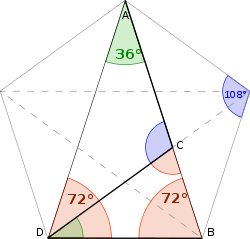
Matematičari još od Euklida su proučavali svojstva zlatnog odnosa, uključujući pojavljivanje u dimenzijama pravilnog petougla i u zlatnom pravougaoniku, koji može da se podeli u kvadrat i još jedan pravougaonik istog odnosa.

Istorija

Teorija zlatnog preseka započeta je u antici, a svoj procvat imala je u renesansi kada su umetnici, matematičari, fizičari i astrolozi tražili savršenstvo u kompozicijama poznatih struktura.

Herodot (484. - 424. p. n. e.) je zapisao: „Jedan egipatski sveštenik govoreći o obliku Keopsove piramide spomenuo mi je da je kvadrat nad njenom visinom jednak površini bočnog trougla.”

Matematička piramida

$v={\frac {a}{2}}{\sqrt {\varphi }}$

$b={\frac {a}{2}}{\sqrt {\varphi +2}}$

$\alpha =\operatorname {arctg} {\sqrt {\varphi }}$

$\beta =\operatorname {arctg} {\sqrt {\frac {\varphi }{2}}}$

Grčki kipar Fidije u V veku p. n. e. primenio je zlatni presek u dizajnu svojih skulptura i gradnji Partenona. Platon (grčki filozof, V i IV vek pne) u „Timoteju” opisuje pet pravilnih geometrijskih tela kao osnovu harmonične strukture sveta. Zlatni presek igra ključnu ulogu u dimenzijama i oblikovanju nekih od ovih tela. Pitagorejci (oko 500. godine p. n. e.) dolaze do jednog od najvažnijih otkrića u matematici: dijagonala i stranica kvadrata (pravilnog petougla) su nesamerljive.

Zlatni trougao unutar zlatnog trougla

${\frac {d}{a_{5}}}=\varphi$

Grčki matematičar Euklid prvi je ovaj broj uočio i matematički izrazio. Oko 300 godina p. n. e. napisao je knjigu „Elementi” u kojoj navodi prvu zabeleženu definiciju zlatnog preseka.

Data dužina se može podeliti tako da pravougaonik obuhvaćen celom dužinom i jednim odsečkom, bude jednak kvadratu na drugom odsečku.

$a(a-x)=x^{2}$

$x^{2}+ax-a^{2}=0$

$x={\frac {-1+{\sqrt {5}}}{2}}a$

Sva znanja starih Grka objedinio je rimski arhitekta Marko Vitruvije u delu De architectura libri decem ili Deset knjiga o arhitekturi, posvećenom imperatoru Avgustu. Pisao je o simetriji hramova, a njihove proporcije upoređuje s razmerama čovečijeg tela. Vitruvije je ucrtao ljudsko telo u kružnicu, što je kasnije ponovo interpretirao Leonardo Da Vinči. Luka Pačoli (1446–1510) štampao je u Veneciji 1509. delo De divina proportione, koje je imalo veliki uticaj i nakon kojeg zlatni presek doživljava pravu renesansu. U njemu opisuje harmonijske osobine „božanske razmere”. Knjigu je ilustrovao Leonardo da Vinči.

Martin Om je 1835. godine u drugom izdanju udžbenika Die reine Elementar - Mathematik (Čista elementarna matematika) prvi put koristi termin zlatni presek. Oznaku $\varphi$ je 1909. predložio američki matematičar Mark Bar u čast slavnog starogrčkog kipara Fidije (480–430. p. n. e.)

Proračun

Binarni	1.1001111000110111011...
Dekadni	1.6180339887498948482...  A001622
Heksadecimalni	1.9E3779B97F4A7C15F39...
Verižni razlomak	$1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}}}$
Algebarski oblik	${\frac {1+{\sqrt {5}}}{2}}$
Beskonačni red	${\frac {13}{8}}+\sum _{n=0}^{\infty }{\frac {(-1)^{(n+1)}(2n+1)!}{(n+2)!n!4^{(2n+3)}}}$

Dve veličine a i b su u zlatnom odnosu φ ako

${\frac {a+b}{a}}={\frac {a}{b}}=\varphi .$

Jedan metod za pronalaženje vrednosti φ je sa rešavanjem leve strane. Uprošćavanjem razlomka i zamenom u b/a = 1/φ,

${\frac {a+b}{a}}=1+{\frac {b}{a}}=1+{\frac {1}{\varphi }}.$

Stoga je,

$1+{\frac {1}{\varphi }}=\varphi .$

Množenjem sa φ daje

$\varphi +1=\varphi ^{2}$

koje može da se izrazi kao

${\varphi }^{2}-\varphi -1=0.$

Korišćenjem formule za rešavanje kvadratne jednačine, dobijaju se dva rešenja:

$\varphi ={\frac {1+{\sqrt {5}}}{2}}=1.61803\,39887\dots$

i

$\varphi ={\frac {1-{\sqrt {5}}}{2}}=-0.6180\,339887\dots$

Zato što je φ odnos između dve pozitivne vrednosti, φ je uvek pozitivna vrednost:

$\varphi ={\frac {1+{\sqrt {5}}}{2}}=1.61803\,39887\dots$.

Algebra

Iracionalnost

Zlatni odnos je iracionalan broj. Ispod su dva kratka dokaza o iracionalnosti:

Kontradikcija izrazu u najnižoj vrednosti

Da je φ racionalan broj, onda bi bio omer stranama pravougaonika sa celim stranama (pravougaonik koji obuhvata ceo dijagram). Ali bi takođe bio i odnos celobrojnih strana manjeg pravougaonika (desni deo dijagrama) dobijen brisanjem kvadrata. Sekvenca smanjenja celobrojne vrednosti dužine stranice formirane brisanjem kvadrata ne može večno trajati jer celi brojevi imaju donje granice, stoga φ ne može biti racionalan.

Podsetimo se da:

celina je duži deo plus kraći deo;

celina je duži deo kao što je duži deo na kraći deo.

Ako celinu imenujemo sa n a duži deo sa m, onda druga izjava postaje:

n je prema m isto kao što je m prema n − m,

ili, algebarski

${\frac {n}{m}}={\frac {m}{n-m}}.\qquad (*)$

Tvrditi da je φ racionalan znači da je φ odnos n/m gde su n i m celi brojevi. Možemo reći i da n/m imaju najniže vrednosti i da su n i m pozitivni brojevi. Ali ako je razlomak n/m u najnižim vrednostima, onda se identitet obeležava sa (*) za gornju jednačinu m/(n − m) koja i dalje poseduje najniže vrednosti. To je kontradikcija koja proizlazi iz tvrdnje da je φ racionalan.

Izvod iz iracionalnosti broja √5

Još jedan kratak dokaz — verovatno poznatiji — gde iracionalnost zlatnog odnosa koristi zatvorenost racionalnih brojeva kod sabiranja i množenja. Ako je $\textstyle {\frac {1+{\sqrt {5}}}{2}}$ racionalan, onda je i $\textstyle 2\left({\frac {1+{\sqrt {5}}}{2}}\right)-1={\sqrt {5}}$ takođe racionalan, što je protivrečno činjenici da je kvadratni koren od ne-kvadrata prirodnog broja iracionalan.

Najmanji polinom

Zlatni odnos je takođe i algebarski broj a čak i algebarski ceo broj (kompleksan broj koji je koren unarnog polinoma). Najmanji polinom glasi:

$x^{2}-x-1$

Zbog člana sa stepenom 2, ovaj polinom u stvari ima dva korena, i druga vrednost je srodnik zlatnom odnosu.

Srodnik zlatnog preseka

Druga korena vrednost najmanjeg polinoma x² - x - 1 je

$-{\frac {1}{\varphi }}=1-\varphi ={\frac {1-{\sqrt {5}}}{2}}=-0.61803\,39887\dots .$

Apsolutna vrednost ove količine (≈ 0.618) odgovara dužini odnosa u obrnutom smeru (dužina kraće strane u odnosu na dužu stranu, b/a), ponekad poznata pod imenom srodnik zlatnog preseka. Označava se velikim slovom fi ($\Phi$):

$\Phi ={1 \over \varphi }=\varphi ^{-1}=0.61803\,39887\ldots .$

Vidi još

• Zlatni pravougaonik

Literatura

• Livio, Mario (2002). The Golden Ratio: The Story of Phi, The World's Most Astonishing Number. New York: Broadway Books. ISBN 978-0-7679-0815-3. 
• Livio, Mario (2003) [2002]. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number (First trade paperback izd.). New York City: Broadway Books. ISBN 978-0-7679-0816-0. 
• Stakhov, Alexey P.; Olsen, Scott (2009). The Mathematics of Harmony: From Euclid to Contemporary Mathematics and Computer Science. Singapore: World Scientific Publishing. ISBN 978-981-277-582-5. 
• Doczi, György (2005) [1981]. The Power of Limits: Proportional Harmonies in Nature, Art, and Architecture. Boston: Shambhala Publications. ISBN 1-59030-259-1. 
• Huntley, H. E. (1970). The Divine Proportion: A Study in Mathematical Beauty. New York: Dover Publications. ISBN 0-486-22254-3. 
• Joseph, George G. (2000) [1991]. The Crest of the Peacock: The Non-European Roots of Mathematics (New izd.). Princeton, NJ: Princeton University Press. ISBN 0-691-00659-8. 
• Sahlqvist, Leif (2008). Cardinal Alignments and the Golden Section: Principles of Ancient Cosmography and Design (3rd Rev. izd.). Charleston, SC: BookSurge. ISBN 1-4196-2157-2. 
• Schneider, Michael S. (1994). A Beginner's Guide to Constructing the Universe: The Mathematical Archetypes of Nature, Art, and Science. New York: HarperCollins. ISBN 0-06-016939-7. 
• Scimone, Aldo (1997). La Sezione Aurea. Storia culturale di un leitmotiv della Matematica. Palermo: Sigma Edizioni. ISBN 978-88-7231-025-0. 
• Walser, Hans (2001) [Der Goldene Schnitt 1993]. The Golden Section. Peter Hilton trans. Washington, DC: The Mathematical Association of America. ISBN 0-88385-534-8. 
• Olsen, Scott (2006). The Golden Section: Nature's Greatest Secret. Glastonbury: Wooden Books. str. 3. ISBN 978-1-904263-47-0. 
• Van Mersbergen, Audrey M., Rhetorical Prototypes in Architecture: Measuring the Acropolis with a Philosophical Polemic, Communication Quarterly, Vol. 46, 1998 ("a 'Golden Rectangle' has a ratio of the length of its sides equal to 1:1.61803+. The Parthenon is of these dimensions.")
• Livio, Mario. „The Golden Ratio in Art: Drawing heavily from The Golden Ratio” (PDF). str. 6. Pristupljeno 11. 9. 2019. 
• Le Corbusier, The Modulor, p. 35, as cited in Padovan, Richard, Proportion: Science, Philosophy, Architecture (1999), p. 320. Taylor & Francis. ISBN 978-0-419-22780-9.: "Both the paintings and the architectural designs make use of the golden section".

Spoljašnje veze

• Hazewinkel Michiel, ur. (2001). „Golden ratio”. Encyclopaedia of Mathematics. Springer. ISBN 978-1556080104. 
• "Golden Section" by Michael Schreiber, Wolfram Demonstrations Project, 2007.
• Golden Section in Photography: Golden Ratio, Golden Triangles, Golden Spiral
• Weisstein, Eric W. „Golden Ratio”. MathWorld. 
• „Researcher explains mystery of golden ratio”. PhysOrg. 21. 12. 2009. .
• Knott, Ron. „The Golden section ratio: Phi”.  Information and activities by a mathematics professor.
• The Pentagram & The Golden Ratio. Green, Thomas M. Updated June 2005. Archived November 2007. Geometry instruction with problems to solve.
• Schneider, Robert P. (2011). „A Golden Pair of Identities in the Theory of Numbers”. arXiv:1109.3216  [math.HO].  Proves formulas that involve the golden mean and the Euler totient and Möbius functions.
• The Myth That Will Not Go Away Arhivirano na sajtu Wayback Machine (12. novembar 2020), by Keith Devlin, addressing multiple allegations about the use of the golden ratio in culture.