Ирационалан број
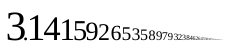
У математици, ирационалан број је онај реалан број који није рационалан број, тј не може бити написан као разломак два цела броја односно није облика
где су a и b цели бројеви и b није једнако нула. Може се лако показати да су ирационални бројеви сви који у свакој бројној основи (децималној, бинарној, итд) имају бесконачно цифара и не долази до бесконачно понављање неког подниза цифара, мада математичари никад ово не би навели као дефиницију.
Скоро сви реални бројеви су ирационални у смислу прецизне дефиниције наведене ниже.
Неки ирационални бројеви су алгебарски бројеви, као што је
- квадратни корен из 2,
- кубни корен из 5
а неки су трансцендентни бројеви, као што су
- природни логаритам броја 2,
- број π, Архимедов број, Лудолфов број,
- математичка константа e, основа природног логаритма, Ојлерова константа.
Ако је однос дужина две дужи ирационалан, дужи су међусобно несамерљиве, што значи да немају заједничку меру. Мера дужи I је таква дуж Ј, да цео број дужи Ј стаје у дуж I. Међу ирационалним бројевима су однос π обима круга и његовог пречника, Ојлеров број e, златни пресек φ и квадратни корен из два.[1] Заправо, сви квадратни корени природних бројева, осим савршених квадрата, су ирационални.[2]
Историја теорије ирационалних бројева[уреди | уреди извор]
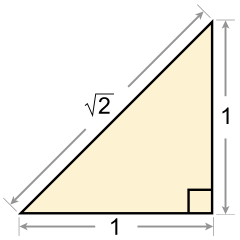
Откриће ирационалних бројева се везује за питагорејце, конкретно за Хипаса из Метапонтума, који је извео (највероватније геометријски) доказ о ирационалности (несамерљивости) квадратног корена из броја 2. Према причи је Хипас покушао да докаже да је хипотенуза једнакокраког правоуглог троугла самерљива са катетом, односно данашњим речником да је корен из 2 могуће представити разломком. Усред тражења таквог доказа он је доказао управо супротно. Питагорејска секта је међу својим догмама имала да је свет у суштини математички и да се све у њему може представити односом бројева. Бројеви који се нису могли представити тако су по њима били ван ума (лат. ratio) односно ван памети, па их је неко тако и назвао, ирационални (грчки алогон, што додуше може значити и оно о чему не треба причати). Хипас је, изгледа, неком ван братства испричао о свом открићу. Побеснела браћа су га уљудно позвала на крстарење и на пучини бацили преко палубе.
У шеснаестом столећу је коначно дошло до прихватања појмова негативни бројеви, целобројни и разломљени део броја. У седамнаестом столећу је коначно прихваћен децимални бројни систем у данашњем облику од шире математичке заједнице. Абрахам де Моавр и Леонард Ојлер, у следећем столећу, откривају изузетно употребљиве особине имагинарног броја. У деветнаестом столећу је комплетирана теорија комплексних бројева, ирационални бројеви су раздвојени на алгебарске и трансцендентне, доказано је постојање трансцендентних бројева и направљен нови приступ у области која је недирнута од доба Еуклида, теорији ирационалних бројева. Године 1872. своје теорије су објавили Карл Вајерштрас, Рихард Дедекинд и Едуард Хајне. Вајерштрасове и Дедекиндове идеје даље разрађују Пинкерле и Танери. Вајерштрас, Кантор и Хајне су свој рад засновали на редовима док је Дедекинд идеју нашао у пресеку осе реалних бројева раздвајајући све рационалне бројеве у две групе одређених особина. Ова тема се даље разрађује кроз радове Вајерштраса, Кронекера и Мереа.
Леонард Ојлер је посветио пажњу верижним разломцима, блиско повезаним са ирационалним бројевима, али се тек у деветнаестом веку детаљно разрађују у делима Жозеф Луј Лагранжа.
Кронекер је први раздвојио трансцендентне бројеве од алгебарских. Ламбер је 1761 доказао да π није рационалан број. Доказао је још да en није рационалан ако је n рационалан (осим за n=0). Лежандр је 1794. године довршио Ламберов доказ и још доказао да π не може бити квадратни корен рационалног броја. Жозеф Лиувил је 1840. године показао да ни е ни е2 не могу бити решења квадратне једначине са целобројним коефицијентима. Постојање трансцендентних бројева је доказао Лиувил 1844. године али је тек 1873. показан један такав. Чарлс Хермит је тада доказао да је е трансцендентан а Линдеман је 1882. године то исто доказао за π полазећи од Хермитових закључака. Линдеманов доказ је поједноставио Вајерштрас 1885. године и Дејвид Хилберт 1893. године а касније су се тиме бавили и Хурвиц и Пол Алберт Гордон.
Ирационалност квадратног корена из 2[уреди | уреди извор]
Један доказ ирационалности квадратног корена из 2 се доказује довођењем у контрадикцију (reductio ad absurdum), омиљеном методом старих Хелена. Тврдња се доказује увођењем супротне претпоставке у односу на жељену и кроз доказни поступак долазимо до контрадикције таквој претпоставци, што је елиминише. Тако је наша жељена претпоставка остала једина могућа те је стога тачна.
- Претпоставимо да је рационалан број. То значи да постоје природни бројеви и такви да је
- Тада може бити написан као нескративи разломак , што значи да су бројеви и узајамно прости природни бројеви и истовремено .
- Sledi da je odakle je .
- Odavde je jasno паран број, јер је представљен као производ броја 2 и природног броја.
- Из овога следи да мора бити паран, јер је квадрат парног броја паран а непарног броја непаран.
- Пошто је паран, постоји такво да важи .
- Кад убацимо последњу једнакост у (3) добијамо: , што води до односно после скраћивања са 2 добијамо .
- Из овога следи да је паран број јер је представљен као производ двојке и природног броја. Потом из овога следи да је и паран јер само парни бројеви имају парне квадрате.
- Из (5) и (8) следи да су и a и b парни, што је у директној супротности са претпоставком у (2) да су бројеви a и b узајамно прости.
Тако смо доказали жељено, прво побијајући ту тврдњу а потом доказујући да нас то доводи до апсурда и контрадикције. Закључак је, не треба негирати почетну тврдњу јер је она тачна. Дакле је ирационалан.
Овај доказ може бити уопштен, да докаже да је било који корен било ког природног броја или природан број или ирационалан.
Другачији доказ[уреди | уреди извор]

Применом исте методе на другачији начин можемо доказати ирационалан је мање познат али завређује да се представи. Дакле, ако је тада се геометријском методом, једноставном лењир и шестар конструкцијом може демонстрирати да је .
Са слике је јасно да су велики и мали правоугли троуглови слични. Ако је однос хипотенузе и катете код великог једнак m/n, где су m и n узајамно прости, тада исти такав однос постоји и код мањег и износи (2n-m)/(m-n). Али пошто смо добили однос у коме су бројеви у разломку мањи него у првом разломку закључак је да смо управо скратили именилац и бројилац, што је у супротности са полазном претпоставком да су m и n узајамно прости.
Ово је доказ у коме нема рачуна већ искључиво геометрије, па се може сматрати прихватљивим старим хеленским геометрима.
Ирационалност златног пресека[уреди | уреди извор]
Када се дуж подели на два дела на начин да се дужи део према целини односи на исти начин као краћи део према дужем, тада смо дуж поделили у златном односу. Каже се још да смо направили златан пресек, чији је однос
Претпоставимо да је овај број рационалан, и представимо га односом n/m где су n и m узајамно прости. Нека је n дужина целине, а m дужина дужег дела. Тада је дужина краћег дела n − m. Следи да је тада
- .
Али ово значи да смо поједноставили разломак који, према претпоставци, није могао бити поједностављен, скраћен. То је контрадикција, значи претпоставка да је φ рационалан није тачна.
Трансцендентни и алгебарски ирационални бројеви[уреди | уреди извор]
Скоро сви ирационални бројеви су трансцендентни а истовремено су сви трансцендентни бројеви ирационални. Познати су следећи примери
- еr је ирационално, ако је r ≠ 0 рационално;
- πr је ирационално, ако је r ≠ 0 рационално;
- еπ је такође ирационално.
Други начин конструкције ирационалног броја је ирационални алгебарски број тј. као нула полинома са целобројним коефицијентима. Пођимо од једначине
- p(x) = an xn + an-1 xn−1 + ... + a1 x + a0 = 0
где су коефицијенти ai цели бројеви. Претпоставимо да постоји реалан број x такав да је p(x) = 0
Једини могући рационални корен овог полинома је облика r/s где је r делилац a0 и s је делилац an. Постоји коначан број кандидата и сви се могу проверити појединачно. Ако ниједан од њих није корен p, тада x мора бити ирационално. Ова техника може бити коришћена да се покаже да је x = (21/2 + 1)1/3 ирационалан, јер тада је (x3 − 1)2 = 2 односно x6 − 2x3 − 1 = 0, а овај полином нема рационалне корене (једини кандидати су ±1).
Зато што алгебарски бројеви чине поље, многи ирационални бројеви могу бити конструисани комбиновањем трансцендентних и алгебарских бројева. На пример 3π+2, π + √2 и e√3 су ирационални (и трансцендентни).
Једноставан доказ ирационалности за неке логаритме[уреди | уреди извор]
Логаритми су вероватно најједноставнији за доказивање ирационалности. Следи доказ свођењем на контрадикцију, да је log23 ирационалан:
- Претпоставимо да је log23 рационалан. Значи постоје природни бројеви m and n, такви да је log23 = m/n.
- Тада је 2m/n = 3.
- Одатле следи 2m = 3n.
- Али 2 на неки природан број је увек парно, а 3 на неки природан број је увек непарно. Следи почетна претпоставка је погрешна.
Случајеви као што је log102 се доказују слично.
Ирационални бројеви и децимални развој[уреди | уреди извор]
Често се погрешно закључује да математичари дефинишу ирационалан број у смислу децималног развоја, називајући број ирационалним ако децимални развој има бесконачно цифара, а цифре се не понављају. Ниједан математичар не узима ово као дефиницију јер избор основе 10 за бројни систем је произвољан а права дефиниција је боља и једноставнија. Мада, истини за вољу, тачно је да је број облика n/m, где су n и m природни бројеви, ако и само ако децимални приказ има коначан број цифара или се цифре понављају бесконачно у групама. Ово је могуће показати обичним школским дељењем n са m јер само m могућих остатака постоји. Ако је 0 остатак, децимални испис се завршава. Ако се 0 никад не појављује тада се поступак може поновити највише m − 1 пута пре него што се поново исти остаци појаве. После тога, остатак се понавља и децималне цифре се понављају. Пример:
Пошто је дужина понављајуће групе цифара 3, помножимо са 103:
и одузмимо A од обе стране:
Тада
(Број 135, из горњег примера, се лако налази употребом Еуклидовог алгоритма.)
Бројеви за које се не зна да ли су ирационални[уреди | уреди извор]
Не зна се да ли су π + e и π − e ирационални или не.
У ствари, не постоје природни бројеви m и n за које се зна да ли је m·π + n·e ирационално или не.
Није познато ни за , , или Ојлер-Машерони гама константу да ли су ирационални.
Скуп ирационалних бројева[уреди | уреди извор]
Скуп ирационалних бројева нема стандардну ознаку као што је то случај са скупом природних бројева N, скупом целих бројева Z, скупом рационалних бројева Q или скупом реалних бројева R.
Скуп ирационалних бројева је непребројив, док је скуп рационалних бројева пребројив а реалних бројева непребројив. Скуп алгебарских ирационалних бројева, значи нетрансцендентних, је пребројив.
Користећи апсолутну вредност за мерење растојања, ирационални бројеви чине метрички простор који није комплетан. Па ипак, овај метрички простор је хомеоморфан комплетном метричком простору свих низова природних бројева; хомеоморфизам је дат бесконачним развојем верижних разломака. Ово показује да у простору ирационалних бројева важи исказ Берове теореме о категорији.
Неки занимљиви ирационални бројеви[уреди | уреди извор]
Константа Коупланд-Ердош
- 0.235711131719232931374143...
добијена спајањем простих бројева у низ јесте ирационалан број. Зна се чак и да је нормалан број.
Референце[уреди | уреди извор]
- ^ The 15 Most Famous Transcendental Numbers. by Clifford A. Pickover. URL retrieved 24 October 2007.
- ^ Jackson, Terence (2011-07-01). „95.42 Irrational square roots of natural numbers — a geometrical approach”. The Mathematical Gazette (на језику: енглески). 95 (533): 327—330. ISSN 0025-5572. S2CID 123995083. doi:10.1017/S0025557200003193.
Литература[уреди | уреди извор]
- Adrien-Marie Legendre, Éléments de Géometrie, Note IV, (1802), Paris
- Rolf Wallisser, "On Lambert's proof of the irrationality of π", in Algebraic Number Theory and Diophantine Analysis, Franz Halter-Koch and Robert F. Tichy, (2000), Walter de Gruyer
- Др Павле Миличић, Мр Владимир Стојановић, Др Зоран Каделбург, Др Бранислав Боричић: МАТЕМАТИКА, За I разред средње школе, Програми са четири часа наставе математике недељно, Друго издање, Завод за издавање уџбеника, Нови Сад, 1992.
- Cantor, Georg (1874). "Über eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen". Journal für die Reine und Angewandte Mathematik, volume 77, pp. 258–62.
- Feferman, Solomon (1989). The Number Systems: Foundations of Algebra and Analysis, AMS Chelsea, ISBN 0-8218-2915-7.
- Katz, Robert (1964). Axiomatic Analysis, D.C. Heath and Company.
- Landau, Edmund (2001). Foundations of Analysis. American Mathematical Society, ISBN 0-8218-2693-X.
- Howie, John M. Real Analysis. Springer, (2005) ISBN 1-85233-314-6.
- Schumacher, Carol (1996), ChapterZero / Fundamental Notions of Abstract Mathematics BV, Addison-Wesley, ISBN 978-0-201-82653-1
- Selin, Helaine; D'Ambrosio, Ubiratan, ур. (2000), Mathematics Across Cultures: The History of Non-western Mathematics, Springer, ISBN 978-1-4020-0260-1
- Matvievskaya, Galina (1987), „The Theory of Quadratic Irrationals in Medieval Oriental Mathematics”, Annals of the New York Academy of Sciences, 500 (1): 253–77 [254], Bibcode:1987NYASA.500..253M, doi:10.1111/j.1749-6632.1987.tb37206.x
- Selin, Helaine; D'Ambrosio, Ubiratan (2000), Mathematics Across Cultures: The History of Non-western Mathematics, Springer, ISBN 978-1-4020-0260-1
- Beckmann, Petr (1993), A History of Pi, Dorset Classic Reprints, Barnes & Noble Publishing, стр. 170, ISBN 978-0-88029-418-8, Архивирано из оригинала 2016-05-04. г., Приступљено 2015-11-15.
- Arndt, Jörg; Haenel, Christoph (2001), Pi Unleashed, Springer, стр. 192, ISBN 978-3-540-66572-4, Архивирано из оригинала 2016-05-21. г., Приступљено 2015-11-15
- Dunham, William (2015), The Calculus Gallery: Masterpieces from Newton to Lebesgue, Princeton University Press, стр. 127, ISBN 978-1-4008-6679-3, Архивирано из оригинала 2015-05-14. г., Приступљено 2015-02-17, „Cantor found a remarkable shortcut to reach Liouville's conclusion with a fraction of the work”
- Hurwitz, Adolf (1893). „Beweis der Transendenz der Zahl e”. Mathematische Annalen (43): 134—35.
- Gordan, Paul (1893). „Transcendenz von e und π”. Mathematische Annalen. 43 (2–3): 222—24. doi:10.1007/bf01443647.
Спољашње везе[уреди | уреди извор]
- Чланак о ирационалним бројевима на MathWorld (језик: енглески)
- Доказ ирационалности корена из 2 (језик: енглески)
- Zeno's Paradoxes and Incommensurability Архивирано 2016-05-13 на сајту Wayback Machine (n.d.). Retrieved April 1, 2008



![{\displaystyle {\sqrt[{3}]{5}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15f23a69b349ab35ccd5dd0d3083549a40fcaebc)




























