Хоризонт догађаја

У општој теорији релативности хоризонт догађаја је уопштени назив за границу у простор-времену, дефинисану у односи на посматрача, иза које догађаји не могу да утичу на посматрача. Овај термин је сковао Волфганг Риндлер током 1950-их.[1] Светло које се емитује унутар хоризонта догађаја не може никада да стигне до посматрача и било шта што пређе преко хоризонта са посматрачеве стране више никада не буде виђено. На пример, црна рупа је окружена хоризонтом догађаја. Једна формалнија дефиниција гласи:
- Хоризонт догађаја је површина замишљене кугле око сферносиметричне расподеле масе из које не може изаћи никакав облик материје или енергије. Полупречник кугле је једнак Шварцшилдовом полупречнику.
Године 1784, Џон Мичел је предложио да у близини компактних масивних објеката гравитација може бити довољно јака да чак ни светлост не може да побегне. У то време доминирала је Њутнова теорија гравитације и такозвана корпускуларна теорија светлости. У овим теоријама, ако брзина надвладавања гравитационог утицаја масивног објекта прелази брзину светлости, тада светлост која потиче из њега може привремено побећи, али ће се вратити. Године 1958. Дејвид Финкелстајн је употребио општу релативност да уведе строжију дефиницију локалног хоризонта догађаја у црној рупи као границу изван које догађаји било које врсте не могу утицати на спољног посматрача. То је довело до парадокса информација и заштитног зида, који су подстакли преиспитивање концепта хоризонта локалних догађаја и појма црних рупа. Касније је развијено неколико теорија, неке са хоризонтима догађаја, а неке без њих. Стивен Хокинг, који је био један од водећих развијача теорија за описивање црних рупа, предложио је да се уместо хоризонта догађаја користи привидни хоризонт, рекавши да „гравитациони колапс производи привидне хоризонте, али нема хоризоната догађаја”. На крају је закључио да „одсуство хоризонта догађаја значи да не постоје црне рупе - у смислу режима из којих светлост не може побећи у бесконачност.“[2][3]
Чини се да сваки објекат који се приближава хоризонту са стране посматрача успорава и никада сасвим не прелази хоризонт.[4] Због гравитационог црвеног помака, његова слика временом поприма црвену боју док се објекат удаљава од посматрача.[5]
Својства[уреди | уреди извор]
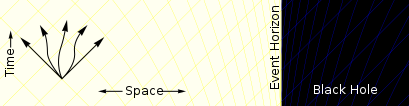 Далеко од црне рупе, честица се може кретати у било ком смеру. Ограничена је само брзином светлости. |
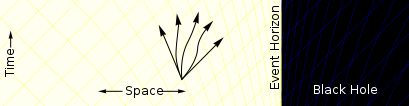 Ближе црној рупи простор-вријеме почиње да се деформише. У неким погодним координатним системима, више стаза иде ка црној рупи него стаза које се удаљавају.[Note 1] |
 Унутар хоризонта догађаја сви будући временски путеви приближавају честицу центру црне рупе. Више није могуће да честица побегне, без обзира у ком правцу честица путује. |
Хоризонт догађаја раздваја простор на два дела између којих је немогућа комуникација: простор унутар и изван хоризонта догађаја.
- Кретање у простору изван хоризонта догађаја: Ако посматрамо свемирски брод које пада према црној рупи, на њему опажамо временску дилатацију узроковану гравитационим закривљењем простора око црне рупе. Другим речима, нама као удаљеном посматрачу се чини као да време на свемирском броду све спорије и спорије тече. Када свемирски брод дође до хоризонта догађаја, нама се чини као да је на свемирском броду време стало, тј. било који коначни интервал времена на свемирском броду бесконачно траје за удаљеног посматрача.
- Кретање у простору унутар хоризонта догађаја: Било које тело које се нађе унутар хоризонта догађаја нужно пре или касније завршава у средишњем сингуларитету. То значи да је немогуће изаћи изван хоризонта догађаја.
Хоризонт догађаја црне рупе[уреди | уреди извор]
Један од најпознатијих примера хоризонта догађаја потиче из општег релативностичког описа црне рупе, небеског објекта толико густог да оближња материја или зрачење не могу побећи из његовог гравитационог поља. Често се ово описује као граница унутар које је брзина изласка из црне рупе већа од брзине светлости. Међутим, детаљнији опис је да су унутар овог хоризонта све светлости сличне путање (путеви којима би светлост могла кренути), те отуда и све путање у светлосним конусима честица унутар хоризонта, закривљене тако да падају даље у рупу. Када се честица нађе унутар хоризонта, кретање у рупу је неизбежно као и кретање напред у времену - без обзира у ком правцу честица путује - и заправо се може сматрати еквивалентним томе, у зависности од координатног система простор-времена који се користи.[7][8][9][10]
Према основним моделима гравитационог колапса,[11] хоризонт догађаја се формира пре сингуларности црне рупе. Ако би се све звезде у Млечном путу постепено агрегирале према галактичком центру, задржавајући пропорционалне удаљености једна од друге, све би пале у свој заједнички Шварцшилдов радијус много пре него што буду присиљене да се сударају.[3] Све до колапса у далекој будућности, посматрачи у галаксији окружени хоризонтом догађаја нормално би наставили свој живот.
Хоризонт догађаја црне рупе је телеолошке природе, што значи да се мора познавати цео будући простор-време универзума да би се одредила тренутна локацију хоризонта, што је у суштини немогуће. Због чисто теоријске природе границе хоризонта догађаја, путујући објекат не мора нужно доживети чудне ефекте и, заправо, пролази кроз прорачунску границу у правом времену.[12]
Види још[уреди | уреди извор]
Напомене[уреди | уреди извор]
- ^ Скуп могућих путања, тачније будући светлосни конус који садржи све могуће светске линије (на овом дијаграму представљен жуто/плавом мрежом), нагнут је на овај начин у координатама Едингтон–Финкелстајна (овај дијаграм је скицирана верзија Едингтон-Финкелстајновог координатног дијаграма), али у другим координатама светлосни конуси се не нагињу на овај начин, на пример у Шварцшилдовим координатама они се једноставно сужавају без нагињања како се приближавају хоризонту догађаја, а у Крускал–Секерешовим светлосним конусима се уопште не мењају облик или оријентација.[6]
Референце[уреди | уреди извор]
- ^ Rindler, W. (1956-12-01). [Also reprinted in Gen. Rel. Grav. 34, 133–153 (2002), accessible at https://doi.org/10.1023/A:1015347106729.]. „Visual Horizons in World Models”. Monthly Notices of the Royal Astronomical Society. 116 (6): 662—677. ISSN 0035-8711. doi:10.1093/mnras/116.6.662
 .
.
- ^ Hawking, S.W. (2014). „Information Preservation and Weather Forecasting for Black Holes”. arXiv:1401.5761v1
 [hep-th].
[hep-th].
- ^ а б Curiel, Erik (2019). „The many definitions of a black hole”. Nature Astronomy. 3: 27—34. Bibcode:2019NatAs...3...27C. S2CID 119080734. arXiv:1808.01507
 . doi:10.1038/s41550-018-0602-1.
. doi:10.1038/s41550-018-0602-1.
- ^ Chaisson, Eric (1990). Relatively Speaking: Relativity, Black Holes, and the Fate of the Universe
 . W. W. Norton & Company. стр. 213. ISBN 978-0393306750.
. W. W. Norton & Company. стр. 213. ISBN 978-0393306750.
- ^ Bennett, Jeffrey; Donahue, Megan; Schneider, Nicholas; Voit, Mark (2014). The Cosmic Perspective. Pearson Education. стр. 156. ISBN 978-0-134-05906-8.
- ^ Misner, Thorne & Wheeler 1973, стр. 848. sfn грешка: више циљева (2×): CITEREFMisnerThorneWheeler1973 (help)
- ^ Hawking, S.W.; Ellis, G.F.R. (1975). The Large Scale Structure of Space-Time. Cambridge University Press.
- ^ Misner, Charles; Thorne, Kip S.; Wheeler, John (1973). Gravitation. W. H. Freeman and Company. ISBN 978-0-7167-0344-0.
- ^ Wald, Robert M. (1984). General Relativity
 . Chicago: University of Chicago Press. ISBN 978-0-2268-7033-5.
. Chicago: University of Chicago Press. ISBN 978-0-2268-7033-5.
- ^ Peacock, J.A. (1999). Cosmological Physics. Cambridge University Press. ISBN 978-0-511-80453-3. doi:10.1017/CBO9780511804533.
- ^ Penrose, Roger (1965). „Gravitational collapse and space-time singularities”. Physical Review Letters. 14 (3): 57. Bibcode:1965PhRvL..14...57P. doi:10.1103/PhysRevLett.14.57.
- ^ Joshi, Pankaj; Narayan, Ramesh (2016). „Black Hole Paradoxes”. Journal of Physics: Conference Series. 759 (1): 12—60. Bibcode:2016JPhCS.759a2060J. S2CID 118592546. arXiv:1402.3055
 . doi:10.1088/1742-6596/759/1/012060.
. doi:10.1088/1742-6596/759/1/012060.
Литература[уреди | уреди извор]
- The Universe in a Nutshell by Stephen Hawking
- Abhay Ashtekar and Badri Krishnan, “Isolated and Dynamical Horizons and Their Applications”, Living Rev. Relativity, 7, (2004), 10; Online Article, cited Feb.2009.
- Ferguson, Kitty (1991). Black Holes in Space-Time. Watts Franklin. ISBN 978-0-531-12524-3.
- Hawking, Stephen (1988). A Brief History of Time. Bantam Books, Inc. ISBN 978-0-553-38016-3.
- Hawking, Stephen; Penrose, Roger (1996). The Nature of Space and Time. Princeton University Press. ISBN 978-0-691-03791-2.
- Melia, Fulvio (2003). The Black Hole at the Center of Our Galaxy
 . Princeton U Press. ISBN 978-0-691-09505-9.
. Princeton U Press. ISBN 978-0-691-09505-9. - Melia, Fulvio (2003). The Edge of Infinity. Supermassive Black Holes in the Universe
 . Cambridge U Press. ISBN 978-0-521-81405-8.
. Cambridge U Press. ISBN 978-0-521-81405-8. - Pickover, Clifford (1998). Black Holes: A Traveler's Guide. Wiley, John & Sons, Inc. ISBN 978-0-471-19704-1.
- Thorne, Kip S. (1994). Black Holes and Time Warps. Norton, W. W. & Company, Inc. ISBN 978-0-393-31276-8.
- Susskind, Leonard (2008). The Black Hole War: My Battle with Stephen Hawking to Make the World Safe for Quantum Mechanics. Little, Brown and Company. ISBN 978-0316016407.
- Wheeler, J. Craig (2007). Cosmic Catastrophes (2nd изд.). Cambridge University Press. ISBN 978-0-521-85714-7.
- Carroll, Sean M. (2004). Spacetime and Geometry. Addison Wesley. ISBN 978-0-8053-8732-2., the lecture notes on which the book was based are available for free from Sean Carroll's website.
- Carter, B. (1973). „Black hole equilibrium states”. Ур.: DeWitt, B. S.; DeWitt, C. Black Holes.
- Chandrasekhar, Subrahmanyan (1999). Mathematical Theory of Black Holes. Oxford University Press. ISBN 978-0-19-850370-5.
- Frolov, Valeri P.; Novikov, Igor D. (1998). Black Hole Physics. Fundamental Theories of Physics. 96. ISBN 978-0-7923-5146-7. doi:10.1007/978-94-011-5139-9.
- Frolov, Valeri P.; Zelnikov, Andrei (2011). Introduction to Black Hole Physics. Oxford: Oxford University Press. ISBN 978-0-19-969229-3. Zbl 1234.83001.
- Hawking, S. W.; Ellis, G. F. R. (1973). Large Scale Structure of space time. Cambridge University Press. ISBN 978-0-521-09906-6.
- Melia, Fulvio (2007). The Galactic Supermassive Black Hole. Princeton U Press. ISBN 978-0-691-13129-0.
- Misner, Charles; Thorne, Kip S.; Wheeler, John (1973). Gravitation. W. H. Freeman and Company. ISBN 978-0-7167-0344-0.
- Taylor, Edwin F.; Wheeler, John Archibald (2000). Exploring Black Holes. Addison Wesley Longman. ISBN 978-0-201-38423-9.
- Wald, Robert M. (1984). General Relativity. University of Chicago Press. ISBN 978-0-226-87033-5.
- Wald, Robert M. (1992). Space, Time, and Gravity: The Theory of the Big Bang and Black Holes. University of Chicago Press. ISBN 978-0-226-87029-8.
- Price, Richard; Creighton, Teviet (2008). „Black holes”. Scholarpedia. 3 (1): 4277. Bibcode:2008SchpJ...3.4277C. doi:10.4249/scholarpedia.4277
 .
. - Gallo, Elena; Marolf, Donald (2009). „Resource Letter BH-2: Black Holes”. American Journal of Physics. 77 (4): 294—307. Bibcode:2009AmJPh..77..294G. S2CID 118494056. arXiv:0806.2316
 . doi:10.1119/1.3056569.
. doi:10.1119/1.3056569. - Hughes, Scott A. (2005). „Trust but verify: The case for astrophysical black holes”. arXiv:hep-ph/0511217
 . Lecture notes from 2005 SLAC Summer Institute.
. Lecture notes from 2005 SLAC Summer Institute.
Спољашње везе[уреди | уреди извор]
- Stanford Encyclopedia of Philosophy: "Singularities and Black Holes" by Erik Curiel and Peter Bokulich.
- Black Holes: Gravity's Relentless Pull



