Princip uključenja i isključenja

Unija skupova A i B

U kombinatorici (kombinatorna matematika), princip uključenja i isključenja je tehnika brojanja koja generalizuje poznati metod dobijanja broja elemenata u uniji dva konačna skupa; simbolično izražena kao

$|A\cup B|=|A|+|B|-|A\cap B|,$

gde su A i V dva konačna kompleta skupa i |S| ukazuje na kardinalnost skupa S (koji se može smatrati kao broj elemenata skupa, ako je skup konačan). Formula izražava činjenicu da  zbir veličine dva skupa može biti preveliki, jer neki elementi mogu da se dva puta broje. Dvostruko-računati elementi su oni na preseku dva skupa, a datoteka se koriguje oduzimanjem veličine preseka.

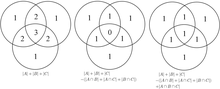
Princip se jasnije vidi u slučaju tri skupa, koji za skupove A, B i C je dat

$|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|.$

Ova formula se može potvrditi brojanjem, koliko puta svaki region u Venov dijagram na slici je uključen u desnu stranu formule. U ovom slučaju, kada se uklone doprinosi nad-prebrojanih elemenata, broj elemenata u međusobnom preseku tri skupa se oduzima suviše često, tako da mora da se doda nazad da se dobije tačna suma.

Princip uključenja i isključenja prikazan Venovim dijagramom sa tri skupa

Generalizacija rezultata ovih primera daje princip uključivanja i isključivanja. Da biste pronašli kardinalnost ujedinjenja n setova:

1. Uključiti kardinalnosti tih skupova.
2. Isključuje kardinalnosti tih parova preseka.
3. Uključiti kardinalnosti trostruko-mudrih preseka. 
4. Isključuje kardinalnosti četvorostruko-mudrih preseka.
5. Uključiti kardinalnosti petostuko-mudrih preseka. 
6. Nastavite, dok kardinalnost na n-torka-mudrom preseku je uključena (ako je n neparan) ili isključena (čak i n).

Naziv potiče od ideje da se princip zasniva na preko-velikodušnom uključivanju, a zatim i na kompenzaciji isključivanja. Ovaj koncept se pripisuje Abrahamu de Moavru (1718); ali se prvi put pojavljuje u novinama Daniela da Silve (1854), a kasnije u radu Dž.J. Silvestera (1883). Ponekad princip se naziva formula Da Silve, ili Silvestera zbog ovih publikacija. Princip je primer metode sito koja se koristi u teoriji brojeva i ponekad naziva sita formula, iako Legendre već koristi sličan uređaj u sito kontekstu u 1808.

Kao konačna verovatnoća računaju se brojanja u odnosu na kardinalnosti verovatnoće prostora, formule za princip uključivanja-isključivanja ostaju na snazi kada se kardinalnosti setova zameni konačnom verovatnoćom. Uopšteno govoreći, obe verzije principa mogu se staviti pod zajedničkim nazivom teorije mere.

U veoma apstraktanom okruženju, principima uključenja-isključenja može se izraziti kao obračun inverzije matrice. Ova inverzna ima posebnu strukturu, što je izuzetno vredna tehnika u kombinatorici i srodnim oblastima matematike. Đan Karlo Rota je rekao:

"Jedan od najkorisnijih principa nabrajanja u diskretnoj verovatnoći i teoriji kombinatorike je proslavljeni princip uključivanja-isključivanja. Kada se vešto primenjuje, ovaj princip je dao rešenje za mnoge kombinatorijalne probleme"

Izjava

U svom opštem obliku, princip uključivanja i isključivanja tvrdi da za konačne skupove A₁, ..., A_n, ima identitet

Svaki termin formule uključivanja i isključivanja postepeno ispravlja brojanje dok se svaki deo na Venovom dijagramu računa tačno jedanput.

Ovo se kompaktno može napisati kao 

${\Biggl |}\bigcup _{i=1}^{n}A_{i}{\Biggr |}=\sum _{k=1}^{n}(-1)^{k+1}\left(\sum _{1\leq i_{1}<\cdots <i_{k}\leq n}\left|A_{i_{1}}\cap \cdots \cap A_{i_{k}}\right|\right)$

${\Biggl |}\bigcup _{i=1}^{n}A_{i}{\Biggr |}=\sum _{\emptyset \neq J\subseteq \{1,2,\ldots ,n\}}(-1)^{|J|-1}{\Biggl |}\bigcap _{j\in J}A_{j}{\Biggr |}.$

Rečima, da bi se računao broj elemenata unije konačnih skupova, prvo sabrati kardinalnosti pojedinačnih setova, a zatim oduzeti broj elemenata koji se pojavljuju u više od jednog skupa, zatim vratiti broj elemenata koji se pojavljuju u više od dva skupa, a zatim oduzeti broj elemenata koji se javljaju u više od tri skupa, i tako dalje. Ovaj proces se završava prirodno, jer ne može biti elemenata koji se pojavljuju u više skupova nego što ima u uniji.

U aplikacijama je uobičajeno da se vidi princip izražen u svojom komplementarnom obliku. To jest, ostavljajući S kao konačan univerzalni skup koji sadrži sve iz  A_i , i dopuštajući da ${\bar {A_{i}}}$ označava komplementno A_i u S, po De Morganovim zakonima

${\biggl |}\bigcap _{i=1}^{n}{\bar {A_{i}}}{\biggr |}={\biggl |}S-\bigcup _{i=1}^{n}A_{i}{\biggr |}=\left|S\right|\;-\sum _{i=1}^{n}\left|A_{i}\right|\;+\sum _{1\leq i<j\leq n}\left|A_{i}\cap A_{j}\right|\;-\;\ldots \ +\;\left(-1\right)^{n}\left|A_{1}\cap \cdots \cap A_{n}\right|.$

Kao još jedan varijanta izjave, neka P1, P2, ..., pn biti lista nekretnina koje elementi skupa S može ili ne može imati, onda je princip uključivanja i isključivanja obezbeđuje način za izračunavanje broja elemenata od S koji imaju ništa od imovine. Samo neka Aj biti podskup elemenata S koji imaju imovinu Pi i koriste princip u komplementarnom obliku. Ova varijanta je zbog Dž.J. Silveste.

Primeri

Brojanje celih brojeva

Kao jednostavan primer upotrebe principa uključivanja-isključivanja, razmotriti pitanje:

Koliko ima celih brojeva u {1,...,100} koji nisu deljivi 2, 3 ili 5?

S = {1,...,100} i P₁ vrednost koja je ceo broj deljiv sa 3, P₂ vrednost koja je ceo broj deljiv sa 3 i P₃ vrednost koja je ceo broj  deljiv sa 5. Neka je A_i podskup od S čiji su elementi vrednosti P_i za koje imamo |A₁| = 50, |A₂| = 33, i |A₃| = 20. Postoji 16 prirodnih brojeva koji su deljivi sa 6, 10 deljiv sa 10 i 6 deljiv sa 15. Konačno, postoje samo 3 cela broja deljiva sa 30, tako da je broj celih brojeva koji nisu deljivi sa 2, 3 ili 5:

100 − (50 + 33 + 20) + (16 + 10 + 6) − 3 = 26.

Brojanje permutacija

Sledeći primer je malo složeniji.

Pretpostavimo da je špil n karata sa  brojevima od 1 do n. Pretpostavimo da kartica numerisana m je u ispravnom položaju ako je mj karticu u palubi. Na koliko načina V se može karta izmešati sa najmanje 1 kartom da bude u pravilnom položaju?

Počnite sa definisanjem skupa AM, koji je sve naloge karata sa m kartom ispravio. Onda je broj naloga, W, sa najmanje jednom kartom koja je u pravilnom položaju, m je

$W={\biggl |}\bigcup _{m=1}^{n}A_{m}{\biggr |}.$

Primeni princip uključivanja-isključivanja,

$W=\sum _{m_{1}=1}^{n}\left|A_{m_{1}}\right|{}-\sum _{1\leq m_{1}<m_{2}\leq n}\left|A_{m_{1}}\cap A_{m_{2}}\right|{}+\sum _{1\leq m_{1}<m_{2}<m_{3}\leq n}\left|A_{m_{1}}\cap A_{m_{2}}\cap A_{m_{3}}\right|{}-\cdots {}+(-1)^{p-1}\sum _{1\leq m_{1}<\cdots <m_{p}\leq n}\left|A_{m_{1}}\cap \cdots \cap A_{m_{p}}\right|\cdots .$

Svaka vrednost $A_{m_{1}}\cap \cdots \cap A_{m_{p}}$  predstavlja skup mešanja koji ima najmanje r vrednosti m₁, ..., m_p u pravilnom položaju. Imajte na umu da je broj mešanja sa najmanje r vrednostima korektnim zavisimo od r, a ne na konkretnim vrednostima m. Na primer, broj mešanja imaju 1., 3. i 17. karte u ispravnom položaju je isti kao i broj mešanja koji imaju 2., 5. i 13. karte u ispravnom položaju. Jedino što je važno da  od n karata, 3 budu izabrane u pravilnom položaju. Dakle postoje ${n \choose p}$ jednakih uslova pri p sabiranju (vidi kombinacije).

$W={n \choose 1}\left|A_{1}\right|-{n \choose 2}\left|A_{1}\cap A_{2}\right|+{n \choose 3}\left|A_{1}\cap A_{2}\cap A_{3}\right|-\cdots +(-1)^{p-1}{n \choose p}\left|A_{1}\cap \cdots \cap A_{p}\right|\cdots .$

$\left|A_{1}\cap \cdots \cap A_{p}\right|$ je broj naredbi koje imaju r elemente u pravilnom položaju, koji je jednak broju načina naredbi preostalih n − p elemenata (n − p)!. Tako smo konačno dobili:

$W={n \choose 1}(n-1)!-{n \choose 2}(n-2)!+{n \choose 3}(n-3)!-\cdots +(-1)^{p-1}{n \choose p}(n-p)!\cdots W=\sum _{p=}^{n}(-1)^{p-1}{n \choose p}(n-p)!.$

Konstatujući da  ${n \choose p}={\frac {n!}{p!(n-p)!}}$, ovo se smanjuje na:

$W=\sum _{p=1}^{n}(-1)^{p-1}\,{\frac {n!}{p!}}.$

Permutacija gde nema karti  u ispravnom položaju se zove poremećaj. Uzimajući n! da je ukupan broj permutacija, verovatnoća Q  nasumično  proizvodi permutacije

$Q=1-{\frac {W}{n!}}=\sum _{p=0}^{n}{\frac {(-1)^{p}}{p!}},$

skraćivanje za n+1 smislu Tejlorove ekspanzije e⁻¹. Tako je verovatnoća pogađanja za mešanje špila karata ili bila netačna gde je svakoj karti 1/e ili 37%.

Poseban slučaj

Situacija koja se pojavljuje u poremećenje primeru iznad javlja dovoljno često da zaslužuje posebnu pažnju. Naime, kada je veličina presek skupova koji se pojavljuju u formulama principa uključivanja-isključivanja zavisi samo od broja skupova u presecima, a ne na kojem postavlja se pojavljuju. Više formalno, ako presek

$A_{J}:=\bigcap _{j\in J}A_{j}$

ima isti kardinalnost, kažu α_k = |A_J|, za svako k-element podgrupa J of {1, ..., n}, a zatim

${\biggl |}\bigcup _{i=1}^{n}A_{i}{\biggr |}=\sum _{k=1}^{n}(-1)^{k-1}{\binom {n}{k}}\alpha _{k}.$

Ili, u komplementarne obliku, gde univerzalnog skupa S ima kardinalnost α₀,

${\biggl |}S\setminus \bigcup _{i=1}^{n}A_{i}{\biggr |}=\sum _{k=0}^{n}(-1)^{k}{\binom {n}{k}}\alpha _{k}.$

Generalizacija

S obzirom na porodicu (ponavljanja dozvoljeno) podskupova A₁, A₂, ..., A_n o univerzalnoj skupu S, princip uključivanja i isključivanja izračunava broj elemenata S u jednoj od ovih podskupovima. Generalizacija ovog koncepta bi izračunati broj elemenata S koje se pojavljuju u tačno neki fiksni m ovih skupova.

Neka je N = [n] = {1,2,...,n}. Ako definišemo $A_{\emptyset }=S$, onda je princip uključivanja i isključivanja može biti napisan kao, koristeći notaciju na prethodnom odeljku; broj elemenata S sadržan u jednoj od A_i je:

$\sum _{J\subseteq [n]}(-1)^{|J|}|A_{J}|.$

Ako je fiksna podskup skupa indeksa N, onda je broj elemenata koji pripadaju A_i za sve i u I i bez drugih vrednosti je:

$\sum _{I\subseteq J}(-1)^{|J|-|I|}|A_{J}|.$

Definisati skupove

$B_{k}=A_{I\cup \{k\}}$ for k in $N\setminus I$.

Tražimo broj elemenata u jednom od BK koji, po principu uključivanja-isključivanja (sa $B_{\emptyset }=A_{I}$), je

$\sum _{K\subseteq N\setminus I}(-1)^{|K|}|B_{K}|.$

Korespondencija K ↔ J = I ∪ K imeđu podskupa N \ I  podskupa N koji sadrži I je bijekcija i ako J i K odgovaraju po ovoj jednjoj karti onda B_K = A_J, pokazuje da je rezultat važeći

U verovatnoći

U verovatnoći, za događaje A₁, ..., A_n u verovatnoći prostora $\scriptstyle (\Omega ,{\mathcal {F}},\mathbb {P} )$, Princip uključivanja-isključivanja postaje za n = 2

$\mathbb {P} (A_{1}\cup A_{2})=\mathbb {P} (A_{1})+\mathbb {P} (A_{2})-\mathbb {P} (A_{1}\cap A_{2}),$

za n = 3

$\mathbb {P} (A_{1}\cup A_{2}\cup A_{3})=\mathbb {P} (A_{1})+\mathbb {P} (A_{2})+\mathbb {P} (A_{3})\qquad {}-\mathbb {P} (A_{1}\cap A_{2})-\mathbb {P} (A_{1}\cap A_{3})-\mathbb {P} (A_{2}\cap A_{3})\qquad {}+\mathbb {P} (A_{1}\cap A_{2}\cap A_{3})$

što može biti napisano u zatvorenoj formi kao

$\mathbb {P} {\biggl (}\bigcup _{i=1}^{n}A_{i}{\biggr )}=\sum _{k=1}^{n}\left((-1)^{k-1}\sum _{\scriptstyle I\subset \{1,\ldots ,n\} \atop \scriptstyle |I|=k}\mathbb {P} (A_{I})\right),$

Kada je poslednji suma ide preko svih podgrupe indeksa sam 1, ..., nk koji sadrže elemente tačno, i

$A_{I}:=\bigcap _{i\in I}A_{i}$

označava presek svih A_i sa indeksom I.

Prema Bonferonijevoj nejednakosti, zbir prvih uslova u formuli je gornja granica Alternativno i donje granice za LHS. Ovo se može koristiti u slučajevima kada je puna formula previše glomazna.

Za opšte mere prostori (S,Σ,μ) i merljive podgrupe A1, ..., An konačne mere, iznad dna identiteta takođe se nalazi verovatnoća mera $\mathbb {P}$ koja je zamenjena merom μ.

Poseban slučaj

Ako se u probabilističkoj verziji principa uključivanje i isključivanja, verovatnoća preseka A_I samo zavisi od I, što znači da za svako k u {1, ..., n} postoji neko a_k takvo da

$a_{k}=\mathbb {P} (A_{I})\quad {\text{for every}}\quad I\subset \{1,\ldots ,n\}\quad {\text{with}}\quad |I|=k,$

tada gornja formula pojednostavljuje to

$\mathbb {P} {\biggl (}\bigcup _{i=1}^{n}A_{i}{\biggr )}=\sum _{k=1}^{n}(-1)^{k-1}{\binom {n}{k}}a_{k}$

zbog kombinatornog tumačenju binomnih koeficijenta $\scriptstyle {\binom {n}{k}}$.

Analogno pojednostavljenje je moguće u slučaju opšta mera prostora (S,Σ,μ) i merljive podgrupe A₁, ..., A_n krajnje mere.

Drugi oblici

Princip ponekad ostaje u formi koja kaže da ako je

$g(A)=\sum _{S\subseteq A}f(S)$

onda je

$f(A)=\sum _{S\subseteq A}(-1)^{\left|A\right|-\left|S\right|}g(S)\qquad (**)$

Sada pokazati štetu i verovatnoće kombinatorni verziju za inkluziju isključenosti principu su slučajevi (**). Uzeti ${\underline {m}}=\{1,2,\ldots ,m\}$, $f({\underline {m}})=0$, i

$f(S)={\bigg |}\bigcap _{i\in {\underline {m}}\backslash S}A_{i}{\bigg \backslash }\bigcup _{i\in S}A_{i}{\bigg |}\qquad {\text{and}}\qquad f(S)=\mathbb {P} {\bigg (}\bigcap _{i\in {\underline {m}}\backslash S}A_{i}{\bigg \backslash }\bigcup _{i\in S}A_{i}{\bigg )}$

respektivno za dve skupove $S$ sa $S\subsetneq {\underline {m}}$. Onda menjamo

$g(A)={\bigg |}\bigcap _{i\in {\underline {m}}\backslash A}A_{i}{\bigg |},~~g({\underline {m}})={\bigg |}\bigcup _{i\in {\underline {m}}}A_{i}{\bigg |}\qquad {\text{and}}\qquad g(A)=\mathbb {P} {\bigg (}\bigcap _{i\in {\underline {m}}\backslash A}A_{i}{\bigg )},~~g({\underline {m}})=\mathbb {P} {\bigg (}\bigcup _{i\in {\underline {m}}}A_{i}{\bigg )}$

respektivno za sve skupove $A$ sa $A\subsetneq {\underline {m}}$. To je zato što elementi $a$ od $\cap _{i\in {\underline {m}}\backslash A}A_{i}$ mogu biti uključeni u drugi $A_{i}$ ($A_{i}$ sa $i\in A$) tako da $\cap \backslash \!\!\cup \!{\text{-}}$formula Upravo prolazi kroz sva moguća produženja skupova $\{A_{i}\mid i\in {\underline {m}}\backslash A\}$ sa drugim $A_{i}$, brojanjem $a$ samo za skupove koji utiču na član $a$, ako $S$ prolazi kroz sve podskupove $A$ (kao u definicji $g(A)$).

Pošto je $f({\underline {m}})=0$, menjamo iz (**) sa $A={\underline {m}}$ tako da

$\sum _{{\underline {m}}\supseteq T\supsetneq \varnothing }(-1)^{\left|T\right|-1}g({\underline {m}}\backslash T)=\sum _{\varnothing \subseteq S\subsetneq {\underline {m}}}(-1)^{m-\left|S\right|-1}g(S)=g({\underline {m}})$

i prepliću se strane, kombinatorna i probabilistička verzija prati princip uključivanja i isključivanja.

Ako se posmatra broj $n$ kao skup svojih glavnih faktora, a zatim (**) je generalizacija Mobius inverzije formule za prirodne beskvadratne brojeve. Dakle, (**) vidi kao Mobius inverzija formule za učestalost algebre delimično određenog skupa svih podskupova A.

Za generalizacija punoj verziji Mobius inverzija formule, (**) mora biti generalizovana. Za više skupova umesto skupova, (**) postaje

$f(A)=\sum _{S\subseteq A}\mu (A-S)g(S)\qquad (***)$

gde je $A-S$ viši skup za svako$(A-S)\uplus S=A$, i

• μ(S) = 1 ako je S skup (skup bez duplih elemenata) parne kardinalnosti.
• μ(S) = −1 ako je S skup (skup bez duplih elemenata) neparne kardinalnosti.
• μ(S) = 0 ako je S pravi (S ima duple elemente).

Uzeti da je $\mu$$(A-S)$ jednako $(-1)^{\left|A\right|-\left|S\right|}$ of (**) u slučaju kada je $A-S$ skup.

Dokaz (***): Zamena

$g(S)=\sum _{T\subseteq S}f(T)$

 na desnoj strani (***). Primetiti da se $f(A)$ pojavljuje na obe strane (***). Moramo pokazati da za svako  $T$ sa $T\subsetneq A$,  $f(T)$ završava se na desnoj strani (***). Tako preporavljeno $T$ tako da $T\subsetneq A$ i uzima prozvoljno $a\in A$ tako da$a\not \in T$.

Primetiti da $A-S$ mora da bude skup za svako pozitivno ili negativno pojavljivanje  $f(T)$ na desnoj strani (***) koje se dobija od $S$ tako da je $T\subseteq S\subseteq A$. Sada za svako pojavljivanje $f(T)$ na desnoj strani (***) dobija se od $S$ tako da je $A-S$ skup koji uključuje $a$ poništava sa onim što se dobija putem odgovarajuće $S$ tako da $A-S$ je skup koji ne uključuje $a$. Ovo će dati željeni rezultat.

Aplikacije

Princip uključivanja i isključivanje je u širokoj upotrebi i ovde se samo nekoliko aplikacija pominje.

Brojanje permutacija elemenata skupa

Poznata primena principa uključivanja i isključivanja je kombinatorni problem računajući sve poremećaje o konačnom skupu. Brojanje permutacija elemenata skupa A je bijekcija iz A koja nema fiksnih tačaka. Preko principa uključivanja i isključivanja može se pokazati da ako je kardinalnost A jednaka n, onda je broj poremećajima je [n! / e] gde [k] označava najbliži ceo broj x; detaljan dokaz je dostupan ovde i videti odeljak primeri gore.

Prvo pojavljivanje problema brojanje permutacija elemenata skupa u ranoj knjizi o igrama na sreću: Essai d'analyse sur les jeux de hazard  P. R. de Montmorta (1678 – 1719) on je bio poznat kao "Montmortov problem" ili po imenu koje mu je dao "problème des rencontres." Problem je takođe poznat kao hatcheck problem.

Broj permutacija elemenata skupa je poznat kao subfaktorijal od n, napisan !n. Iz toga sledi da ako su sve bijekcije dodeljene istoj verovatnoći onda je verovatnoća slučajne bijekcije predstavlja permutacija elemenata skupa koji približno kao 1/e raste ka n.

Brojanje preseka

Princip uključenja i isključenja kombinovan sa De Morganovim zakonima, može se koristiti da se izbroji kardinalnost preseka skupova. Neka $\scriptstyle {\overline {A}}_{k}$ predstavlja dopunu A_k u odnosu na neki univerzalni skup A tako da je $\scriptstyle A_{k}\,\subseteq \,A$ za svako k. Zatim imamo

$\bigcap _{i=1}^{n}A_{i}={\overline {\bigcup _{i=1}^{n}{\overline {A}}_{i}}}$

 okretanje problema pronalaženja preseka u problem pronalaženja unije.

Graf kolorita

Princip isključenja uključenja čini osnovu algoritama za brojne NP-teške grafove pregradnih problema, kao što su grafovi kolorita.

Dobro poznata primena principa je izgradnja hromatskog polinoma grafa.

Biparticioni grafik savršenih poklapanja

Broj savršenih poklapanja biparticionog grafika može biti izračunat koristeći ovaj princip.

Broj "na" funkcije

S obzirom na konačne skupove A i V, koliko sirjektivnih funkcija (na funkcijama) postoji od A do B? Bez ikakvog gubitka opštosti možemo uzeti A = {1,2, ..., k} i V = {1,2, ..., n}, jer je samo kardinalnosti skupova bitna. Korišćenjem S kao skupa svih funkcija od A do B, i definisanje, za svako  i u B, Pi kao "funkcija kojoj nedostaje element  i u B" ( i nije u slici funkcije), princip uključivanja i isključivanja daje broj "na" funkcija između A i B kao:

$\sum _{j=0}^{n}{\binom {n}{j}}(-1)^{j}(n-j)^{k}.$

Permutacije sa zabranjenim pozicijama

Permutacija skupa S = {1,2, ..., n} gde je svaki element S ograničen da ne bude u određenim pozicijama (ovde permutacija se smatra naručivanje od elemenata S) naziva se permutacija sa zabranjenim mestima. Na primer, sa S = {1,2,3,4}, permutacije uz ograničenje da element 1 ne može biti na pozicijama 1 ili 3, i element 2 ne može biti na poziciji 4 su: 2134, 2143, 3124, 4123, 2341, 2431, 3241, 3421, 4231 i 4321. Dajući  da Ai bude skup stavova koji elementu i nisu dozvoljeni da budu u skupu, a Pi da je imovina koja permutacija stavlja element sam u poziciju Ai, princip uključivanja i isključivanja može da se koristi da računaju broj permutacija koje zadovoljavaju sva ograničenja.

U datom primeru, dato je 12 = 2(3!) permutacija sa P₁, 6 = 3! permutacija sa P₂ i nema permutacija za P₃ iliP₄ jer ne postoje ograničenja za ova dva elementa. Broj permutacija zadovoljavaju ograničenja je ovako:

4! − (12 + 6 + 0 + 0) + (4) = 24 − 18 + 4 = 10.

Konačno 4 u ovoj kompilaciji je broj permutacija koje imaju oba svojstva P₁ i P₂. Nema drugih ne-nula doprinosa formuli.

Stirling brojevi druge vrste

Stirling brojevi druge vrste, S (n, k) izračuna broj particija skupa n elemenata u k nepraznim podskupovima (nerazaznatljive kutije). Eksplicitna formula za njih se može dobiti primenom principa uključivanja-isključivanja u veoma blisko povezanom problem, naime, računajući broj particija od n-skupa u k nepraznom ali se razlikuju kutije (uređenim nepraznim podskupovima). Korišćenje univerzalnog skupa koji se sastoji od svih particija na n-skupu u k(verovatno prazan) prepoznatljive kutije,  A₁, A₂, ..., A_k, i svojstva Pi što znači da particija ima kutiju Ai prazan, princip uključivanja i isključivanja daje odgovor za koji se odnosi rezultat. Podela od k! da ukloni veštačku redosled daje Stirling broj druge vrste:

$S(n,k)={\frac {1}{k!}}\sum _{t=0}^{k}(-1)^{t}{\binom {k}{t}}(k-t)^{n}.$

Top polinomi

Top polinom je generisanje funkcija na više načina da se plasiraju u ne-napad topova na tabli V koja izgleda kao podskup kvadrata sa šahovske table; to jest, ne postoje dva topa koja mogu biti u istom redu ili koloni. Odbor V  je bilo koji podskup od kvadrata pravougaonog odbora sa n redova i kolona n; mi mislimo o tome kao o kvadratu u kojem je jednom dozvoljeno da stavi topa. Koeficijent, r_k(B) od x^k u topu polinomaR_B(x) je broj načina k topova, od kojih nijedan ne napada drugog, da se mogu organizovati u trgovima B. Za bilo koji odbora B, postoji komplementarni odbor B "koji se sastoji od kvadrata pravougaonog odbora koji nisu u B, ova komplementarna ploča ima topa polinoma R_B' (x) sa koeficijentima r_k(B').

Ponekad je zgodno da bi mogao da izračuna najviši koeficijent topa polinoma u smislu koeficijenata polinoma topa komplementarnog odbora. Bez gubitka opštosti možemo pretpostaviti da je n ≤ m, pa je koeficijent r_n(B). Broj načina da postavite n koji ne napadaju topove na  n × m tabli (bez obzira o tome da li su smešteni u topu kvadrata na ploči B) je dat kao faktorijelski pad:

$(m)_{n}=m(m-1)(m-2)\cdots (m-n+1).$

Pustiti da P_i ima zadatak n ne napada topova na kompletnoj tabli ima topa u kolumni  i koja nije u kvadratu table B, onda po principu uključivanja i isključivanja imamo:

$r_{n}(B)=\sum _{t=0}^{n}(-1)^{t}(m-t)_{n-t}\;r_{t}(B').$

Ojlerova fi funkcija

Ojlerova fi funkcija, φ(n) je aritmetička funkcija koja prebrojava pozitivne cele brojeve manje ili jednake n koji su relativno prost sa n. To jest, ako je  n pozitivan  broj, onda  φ(n) je broj brojeva k u domenu 1 ≤ k ≤ n koje nemaju zajednički faktor sa n osim 1. Princip uključivanja i isključivanja se koristi za dobijanje formule φ(n). Neka je S skup  {1,2,...,n} i definiše P_i kao broj u skupu S koji je deljiv sa prostim brojem p_i, za 1 ≤ i ≤ r, gde je rastavljanje na faktore od 

$n=p_{1}^{a_{1}}p_{2}^{a_{2}}\cdots p_{r}^{a_{r}}.$

Onda,

$\phi (n)=n-\sum _{i=1}^{r}{\frac {n}{p_{i}}}+\sum _{1\leq i<j\leq r}{\frac {n}{p_{i}p_{j}}}-\cdots =n\prod _{i=1}^{r}\left(1-{\frac {1}{p_{i}}}\right).$

Ublaženi princip uključenja i isključenja

U mnogim slučajevima gde bi princip mogao dati tačnu formulu (posebno, računajući proste brojeve koristeći Eratostenovo sito), formula koja proizilazi ne nudi korisne sadržaje jer je broj termina u njoj preteran. Ako se svaki termin pojedinačno može precizno proceniti, akumulacija grešaka može da implicira da formula uključivanja i isključivanja nije direktno primenjiva. U teoriji brojeva, ovu teškoću razmatrao je Vigo Bran. Nakon sporog početka, njegove ideje su preduzete od strane drugih, i metoda sita je razvijena. Na primer može pokušati da nađe gornju granicu za "prošarane" skupove, a ne tačnu formulu.

Neka su A₁, ..., A_n proizvoljni skupovi i  p₁, ..., p_n realni brojevi u zatvorenom intervalu [0,1]. Onda za svaki paran broj k u {0, ..., n}, indikator funkcije zadovoljava nejednakost:

$1_{A_{1}\cup \cdots \cup A_{n}}\geq \sum _{j=1}^{k}(-1)^{j-1}\sum _{1\leq i_{1}<\cdots <i_{j}\leq n}p_{i_{1}}\dots p_{i_{j}}\,1_{A_{i_{1}}\cap \cdots \cap A_{i_{j}}}.$

Ako je k paran, zameniti  "≥" sa "≤".

Dokaz glavne izjave

Izaberite element sadržan u ujedinjenje svih skupova i neka $A_{1},A_{2},\dots ,A_{t}$ biti individualni setovi koji ga sadrže. (Imajte na umu da T> 0.) Pošto je element broji upravo jednom od levoj strani jednačine (1), moramo da pokažemo da se računa upravo jednom od desne strane. Sa desne strane, jedini ne-zero doprinosi javljaju kada su sve Podskupovi u određenom roku sadrže izabrani element, to jest, svi podskupovi su odabrana od$A_{1},A_{2},\dots ,A_{t}$. Doprinos je jedan za svaki od ovih setova (plus ili minus u zavisnosti od termina) i zato je samo (potpisao) broj ovih podskupova koji se koriste u roku. Onda imamo:

Po binomnoj teoremi,

$0=(1-1)^{t}={\binom {t}{0}}-{\binom {t}{1}}+{\binom {t}{2}}-\cdots +(-1)^{t}{\binom {t}{t}}$.

Koristeći se činjenicom da je  ${\binom {t}{0}}=1$ i preuređenjem uslova, imamo

$1={\binom {t}{1}}-{\binom {t}{2}}+\cdots +(-1)^{t+1}{\binom {t}{t}},$

and so, the chosen element is counted only once by the right-hand side of equation (1).

Algebarski dokaz

Algebarski dokaz može se dobiti pomoću funkcije indikatora (karakteristične funkcije podskupova skupa). Indikator funkcija podskupa S skupa X je funkcija

$\mathbf {1} _{S}\colon X\to \{0,1\}\,$

definisano kao

$\mathbf {1} _{S}(x):={\begin{cases}1&{\text{if }}x\in S,\\0&{\text{if }}x\notin S.\end{cases}}$

Pisanje slaganja dva indikatora funkcije kao proizvoda, imamo da, ako su $A$ i $B$ podskupovi $X$, onda je

$\mathbf {1} _{A}\cdot \mathbf {1} _{B}=\mathbf {1} _{A\cap B}.$

Neka A označava uniju  ${\textstyle \cup _{i=1}^{n}A_{i}}$ skupova A₁, ..., A_n. Da bi se dokazao princip uključenja i isključenja u potpunosti, prvo se proveri identitet

za indikator funkcije, gde je

$A_{I}=\bigcap _{i\in I}A_{i}.$

Sledeća funkcija je jednaka nuli

$(1_{A}-1_{A_{1}})(1_{A}-1_{A_{2}})\cdots (1_{A}-1_{A_{n}})\,=\,0,$

jer: ako je h nije u A, onda svi su faktori 0 - 0 = 0; i na drugi način, ako h ne pripada nekom  A_m onda odgovarajući m faktor je 1 - 1 = 0. proširenje proizvoda na levoj strani, jednačina (*) sledi.

Da bi dokazao princip uključenja i isključenja za kardinalnost skupova, sumiramo jednačine (*) nad svim h u uniji A₁, ..., A_n. Za izvođenje verzije korišćene u verovatnoći, uzmi očekivanja u (*). U principu, integrišite jednačinu (*) u odnosu na μ. Uvek koristite linearnost u ovim izvođenjima.

Vidi još

• Principi kombinatorike
• Bulova nejednakost
• Problem ogrlice
• Schuette–Nesbitt formula
• Identiteti maksimum i minimum

Literatura

• Allenby, R.B.J.T.; Slomson, Alan . How to Count: An Introduction to Combinatorics, Discrete Mathematics and Its Applications (2 ed.). . CRC Press. 2010. pp. 51–60. ISBN 978-1-4200-8260-9. 
• Björklund, Andreas; Husfeldt, Thore; Koivisto, Mikko (2009). „Set Partitioning via Inclusion-Exclusion”. SIAM Journal on Computing. 39 (2): 546—563. doi:10.1137/070683933. 
• Brualdi, Richard A. (2010). Introductory Combinatorics (5th izd.). Prentice–Hall. ISBN 978-0-13-602040-0. 
• Cameron, Peter J. (1994). Combinatorics: Topics, Techniques, Algorithms. Cambridge University Press. ISBN 978-0-521-45761-3. 
• Fernández, Roberto; Fröhlich, Jürg; Alan D., Sokal (1992). Random Walks, Critical Phenomena, and Triviality in Quantum Field Theory. Texts an Monographs in Physics, Berlin: Springer-Verlag. ISBN 978-3-540-54358-9.  MR 1219313, Zbl 0761.60061
• Graham, R.L.; Grötschel, M.; Lovász, L. (1995). Hand Book of Combinatorics. 2. MIT Press – North Holland. ISBN 978-0-262-07171-0. CS1 održavanje: Višestruka imena: spisak autora (veza)
• Gross, Jonathan L. (2008). Combinatorial Methods with Computer Applications. Chapman&Hall/CRC. ISBN 978-1-58488-743-0. 
• Hazewinkel, Michiel , "Inclusion-and-exclusion principle", ur. (2001). Encyclopedia of Mathematics. Springer. ISBN 978-1-55608-010-4. CS1 održavanje: Višestruka imena: spisak urednika (veza)
• Mazur, David R. (2010). Combinatorics A Guided Tour. The Mathematical Association of America. ISBN 978-0-88385-762-5. 
• Roberts, Fred S.; Tesman, Barry (2009). Applied Combinatorics (2nd izd.). CRC Press. ISBN 978-1-4200-9982-9. 
• {{Cite book| ref=harv|last=Stanley|first=Richard P.|title=Enumerative Combinatorics Volume I|location=|publisher=Wadsworth & Brooks/Cole|year=1986|isbn=978-0-534-06546-1|pages=}
• van Lint, J.H.; Wilson, R. M. (1992). A Course in Combinatorics. Cambridge University Press. ISBN 978-0-521-42260-4. 

This article incorporates material from principle of inclusion–exclusion on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.